Skillnad mellan versioner av "3.2 Lokala maxima och minima"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 66: | Rad 66: | ||
::<math> f'(x) \, = \, 0,48\,x - 2,4 </math> | ::<math> f'(x) \, = \, 0,48\,x - 2,4 </math> | ||
| − | | + | Vi vet att derivatan <math> f' \, </math> byter förtecken från <math> - </math> till <math> + </math> mellan kl 4 och 7, dvs någon gång mellan kl 4 och 7 - vi vet inte än när, därför ? - måste derivatan vara <math> 0 \, </math>, eftersom <math> f'(x) \, </math> är en kontinuerlig funktion och måste, för att byta förtecken, gå genom <math> 0 \, </math>: |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
::::<math> f'(4) \, < \, 0 </math> | ::::<math> f'(4) \, < \, 0 </math> | ||
| Rad 92: | Rad 84: | ||
Alltså är <u>nattens kallaste tidpunkt kl 5</u>. | Alltså är <u>nattens kallaste tidpunkt kl 5</u>. | ||
| − | + | b) Temperaturen vid kl <math> 5 \, </math> är: | |
::<math> f(5) = 0,24 \cdot 5^2 - 2,4 \cdot 5 + 7 = 1 </math> | ::<math> f(5) = 0,24 \cdot 5^2 - 2,4 \cdot 5 + 7 = 1 </math> | ||
| Rad 98: | Rad 90: | ||
Alltså är <u>nattens lägsta temperatur 1 grad Celsius</u>. | Alltså är <u>nattens lägsta temperatur 1 grad Celsius</u>. | ||
| − | + | c) På bilden till vänster är kurvan <math> {\color{White} x} f(x) = 0,24\,x^2 - 2,4\,x + 7 {\color{White} x} </math> samt tangenterna till den i <math> x = 2 \, , \; x = 5 </math> och <math> x = 7 \, </math> ritade i samma koordinatsystem. | |
Till höger visas grafen till derivatan <math> {\color{White} x} f'(x) = 0,48\,x - 2,4 {\color{White} x} </math> som är en rät linje i ett annat koordinatsystem: | Till höger visas grafen till derivatan <math> {\color{White} x} f'(x) = 0,48\,x - 2,4 {\color{White} x} </math> som är en rät linje i ett annat koordinatsystem: | ||
Versionen från 14 november 2014 kl. 17.30
| <-- Förra avsnitt | Teori | Övningar | --> Nästa avsnitt |
Derivatans nollställen
Med förtecken menas \( \,+\, \) eller \( \,-\, \), ibland även kallat tecken, som står framför ett tal och avgör om talet är positivt eller negativt.
Det är derivatans förtecken som avgör om en funktion är växande eller avtagande.
:
Regler om växande och avtagande:
Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) är växande för \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, {\bf {\color{Red} >}} \, 0 {\color{White} x}. \)
Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) är avtagande för \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, {\bf {\color{Red} <}} \, 0 {\color{White} x}. \)
Där derivatan är positiv växer funktionen. Där derivatan är negativ avtar funktionen.
Vad som händer när derivatan varken är positiv eller negativ utan är \( \, = \, 0 {\color{White} x} \) behandlas i nästa avsnitt.
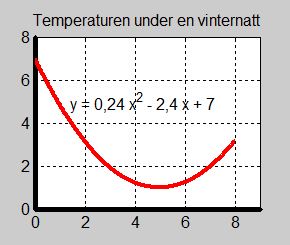
I grafen till exemplet nedan (Temperaturen under en vinternatt) visas en funktion som först avtar (negativ derivata), för att sedan växa (positiv derivata). Men hur avgörs detta algebraiskt?
Exempel 1 Vinternatt
| Under en vinternatt varierar temperaturen enligt funktionen \( {\color{White} x} \; y \, = \, f(x) \, = \, 0,24\,x^2\,-\,2,4\,x\,+\,7 \)
där \( y \; = \) temperaturen i grader Celsius och \( x \; = \) tiden i timmar efter midnatt \(. \qquad\qquad\qquad\qquad \) Definitionsområde: \( \qquad 0 \leq x \leq 8 \) a) Bestäm nattens kallaste tidpunkt. b) Bestäm nattens lägsta temperatur. c) Visualisera dina resultat från a) \( - \) c) i lämpliga grafer. Tolka dina resultat med hjälp av graferna. |
 |
Lösning:
a) För att kunna använda reglerna ovan måste vi bilda derivatan:
- \[ f(x) \, = \, 0,24\,x^2 - 2,4\,x + 7 \]
- \[ f'(x) \, = \, 0,48\,x - 2,4 \]
Vi vet att derivatan \( f' \, \) byter förtecken från \( - \) till \( + \) mellan kl 4 och 7, dvs någon gång mellan kl 4 och 7 - vi vet inte än när, därför ? - måste derivatan vara \( 0 \, \), eftersom \( f'(x) \, \) är en kontinuerlig funktion och måste, för att byta förtecken, gå genom \( 0 \, \):
- \[ f'(4) \, < \, 0 \]
- \[ f'(?) \, = \, 0 \]
- \[ f'(7) \, > \, 0 \]
Detta innebär att temperaturen \( f(x) \, \) byter från att avta till att växa. Härav följer att temperaturen når sitt lägsta värde någon gång mellan kl 4 och 7. Vid denna tidpunkt som är okänd måste derivatan vara \( = \, 0 \). För att få reda på denna tidpunkt sätter vi derivatan till \( \, 0 \) och beräknar tidpunkten \( x \, \):
- \[\begin{array}{rcrcl} f'(x) & = & 0,48\,x - 2,4 & = & 0 \\ & & 0,48\,x & = & 2,4 \\ & & x & = & {2,4 \over 0,48} \\ & & x & = & 5 \end{array}\]
Alltså är nattens kallaste tidpunkt kl 5.
b) Temperaturen vid kl \( 5 \, \) är:
- \[ f(5) = 0,24 \cdot 5^2 - 2,4 \cdot 5 + 7 = 1 \]
Alltså är nattens lägsta temperatur 1 grad Celsius.
c) På bilden till vänster är kurvan \( {\color{White} x} f(x) = 0,24\,x^2 - 2,4\,x + 7 {\color{White} x} \) samt tangenterna till den i \( x = 2 \, , \; x = 5 \) och \( x = 7 \, \) ritade i samma koordinatsystem.
Till höger visas grafen till derivatan \( {\color{White} x} f'(x) = 0,48\,x - 2,4 {\color{White} x} \) som är en rät linje i ett annat koordinatsystem:
Fil:Ex 1 Vinternatt Tangenter.jpg
På bilden till vänster ser man att temperaturen \( f(x) \, \) sjunker från 7 grader Celsius vid midnatt till 1 grad vid kl 5 på morgonen. I hela detta tidsintervall avtar \( f(x) \, \) vilket innebär att derivatan \( f'(x) \, \) är negativ. Ett exempel på det är \( f'(2) = -1,44\, \), dvs tangenten till kurvan i \( x = 2 \, \) har negativ lutning: \( f' < 0\, \).
Vid kl 5 på morgonen har temperaturen \( f(x) \, \) nått sitt minimum på 1 grad Celsius vilket innebär att derivatan \( f'\, \) i denna punkt är 0, dvs tangenten till kurvan i derivatan \( f'(x) \, \) har lutningen 0: \( f'(5) = 0\, \).
Sedan stiger temperaturen \( f(x) \, \) från 1 grad Celsius vid kl 5 till lite under 4 grader Celsius vid kl 8 på morgonen. I hela detta tidsintervall växer \( f(x) \, \) vilket innebär att derivatan \( f'(x) \, \) är positiv. Ett exempel på det är \( f'(7) = 0,96\, \), dvs tangenten till kurvan i \( x = 7 \, \) har positiv lutning: \( f' > 0\, \).
På bilden till höger är endast grafen till derivatan \( f\,'(x) \, \) avbildad. Man ser att den är negativ för alla värden \( x < 5 \, \) och positiv för alla värden \( x > 5 \, \). I \( x = 5 \, \) skär grafen \( \, x-\)axeln, dvs derivatan är 0 \( - \, \) allt i överensstämmelse med resultaten från \( f(x) \, \) på den vänstra bilden. Att grafen till derivatan är en rät linje beror på att den ursprungliga funktionen \( f(x) \, \) är en 2:a gradsfunktion.
