2.7 Numerisk derivering
| << Förra avsnitt | Genomgång | Övningar | Derivering med räknare | Diagnosprov kap 2 Derivatan |
Anta alltid: \( \; \qquad y \; = \; f(x)\, \)
Varför numerisk derivering?
Varför ska vi lära oss numerisk derivering när vi kan derivera med deriveringsregler som bygger på derivatans definition?
Exempel
Följande funktioner matchar inte mot någon av funktionstyperna från vår tabell över deri-
veringsregler och kan därför inte deriveras med de deriveringsregler vi lärt oss hittills:
| \( \quad\; y \, = \, \displaystyle{1 \over x + 1} \qquad\quad \) | \( y \, = \, \displaystyle{1 \over e^x + 1} \qquad\quad \) | \( y \, = \, \ln x \qquad\quad \) |
|
Att inte heller tabellfunktionen bland exemplen ovan kan deriveras med derivatans definition eller någon deriveringsregel, beror på att den är diskret:
Derivatans definition involverar limes som inte kan användas på diskreta utan endast på kontinuerliga funktioner.
Här visas hur man numeriskt deriverar en diskret funktion, se enkelt exempel och Fibonaccifunktionen.
En annan fördel av numerisk derivering (och alla numeriska metoder) är att de enkelt kan programmeras, så:Men vad exakt är numerisk derivering?
derivatan i en punkt utan att behöva använda limes i derivatans definition.
I detta avsnitt behandlas de tre enklaste numeriska deriveringsformlerna:
- Framåtdifferenskvoten
- Bakåtdifferenskvoten
- Centrala differenskvoten
Alla dessa formler baseras på och är modifikationer av den genomsnittliga förändringshastigheten \( \, \displaystyle{\Delta y \over \Delta x} \,\) , även kallad differenskvot.
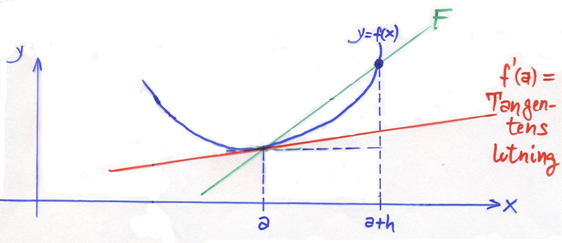
Framåtdifferenskvoten = derivatans definition utan limes
Ett närmevärde till derivatan \( \, f\,'(a) \, \) av funktionen \( \, y = f\,(x) \, \) i punkten \( \, x = a \, \) kan beräknas med
Framåtdifferenskvoten: \( \quad\, f\,'(a) \quad\;\, \approx \displaystyle \quad {f(a + h) \, - \, f(a) \over h} \, = \, {\Delta y \over \Delta x} \)
|
|
Exempel
Följande diskret funktion \( \, f(x) \, \) är given i tabellform. Beräkna \( \, f\,'(0,6) \, \) med framåtdifferenskvoten.
\( x\, \) \( f(x)\, \) \( 0,5\, \) \( 1,79744\, \) \( 0,6\, \) \( 2,04424\, \) \( 0,7\, \) \( 2,32751\, \)
Lösning: Steglängden \( \, h = 0,1\, \) är given i tabellen.
\[ f\,'(0,6) = {f(0,6 + 0,1) - f(0,6) \over 0,1} = {f(0,7) - f(0,6) \over 0,1} = {2,32751 - 2,04424 \over 0,1} = {0,28327 \over 0,1} = 2,8327 \]
I det här fallet är närmevärdet ovan identisk med den exakta lösningen, eftersom det inte finns någon mindre steglängd i tabellen än \( \, h = 0,1 \).
Bakåtdifferenskvoten
Ett närmevärde till derivatan \( \, f\,'(a) \, \) av funktionen \( \, y = f\,(x) \, \) i punkten \( \, x = a \, \) kan beräknas med
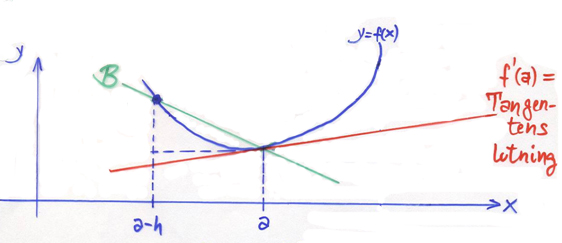
Bakåtdifferenskvoten: \( \quad\, f\,'(a) \qquad\;\, \approx \displaystyle \qquad {f(a) \, - \, f(a-h) \over h} \quad \)
|
|
Här tar man från \( \,a \, \) ett steg \( \,h \, \) bakåt och använder funktionsvärdet före \( \,a \, \) för att beräkna närmevärdet till derivatan i \( \,a \).
Även här gäller: Närmevärdet blir desto bättre ju mindre steglängden \( \, h\, \) väljs.
Exempel
Funktionen \( \, f(x) = \ln x \, \) är given. Välj steglängden \( \, h = 0,01 \, \) och beräkna \( \, f\,'(1,8) \, \) med bakåtdifferenskvoten.
Lösning:
- \[ f\,'(1,8) \approx {f(1,8) - f(1,8 - 0,01) \over 0,01} = {f(1,8) - f(1,79) \over 0,01} = {\ln(1,8) - \ln(1,79) \over 0,01} = 0,5571 \]
Med det exakta resultatet \( \displaystyle f\,'(1,8) = \frac{5}{9} \approx 0,555556 \), avrundat till \( 4 \) decimaler, blir vårt närmevärdes fel:
- Felet \( \, = \, |\,0,5556 \, - \, 0,5571| \, = \, 0,0015\)
Känner man till felet kan man jämföra de olika numeriska deriveringsformlernas noggrannhet, se övning 3.
I fliken Derivering med räknare visas hur man med grafräknaren kan få ett noggrannare närmevärde för \( \, f\,'(1,8) \, \).
Centrala differenskvoten
Ett närmevärde till derivatan \( \, f\,'(a) \, \) av funktionen \( \, y = f\,(x) \, \) i punkten \( \, x = a \, \) kan beräknas med
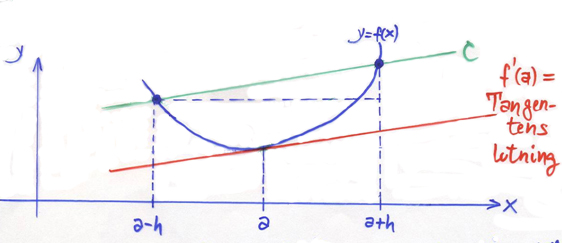
Centrala differenskvoten: \( \quad f\,'(a) \qquad\;\, \approx \displaystyle \qquad {f(a + h) \, - \, f(a-h) \over 2\,h} \quad \)
|
|
Här tar man från \( \,a \, \) både ett steg \( \,h \, \) bakåt och framåt och använder funktionsvärdena före och efter \( \,a \, \) för att beräkna närmevärdet till derivatan i \( \,a \).
Samma sak här: Närmevärdet är desto bättre ju mindre \( \, h\, \) är. Men:
Den centrala differenskvoten är noggrannare än de andra formlerna, se bilden ovan. Ja, det gäller:
För andragradsfunktioner är formeln t.o.m. exakt oavsett \( \,h \).
Exempel
Funktionen \( \, f(x) = x\,^2 \, \) är given. Välj steglängden \( \, h = 0,5 \, \) och beräkna \( \, f\,'(1) \, \) med centrala differenskvoten.
Lösning:
- \[ f\,'(1) \approx {f(1 + 0,5) - f(1 - 0,5) \over 2\cdot 0,5} = {f(1,5) - f(0,5) \over 2\cdot 0,5} = {1,5^2 - 0,5^2 \over 1} = {\color{Red} 2} \]
Funktionens derivata är \( \, f\,'(x) = 2\,x \, \) och därmed är den exakta derivatan \( f\,'(1) = 2 \cdot 1 = {\color{Red} 2} \, \) identisk med den numeriska derivatan.
Noggrannhetsfrågor
Är det en slump att den numeriska deriveringen med centrala differenskvoten i exemplet ovan ger exakt värde, fast steglängden är relativt stor? Svaret är nej:
Sats:
Den centrala differenskvoten ger den exakta derivatan till
alla andragradsfunktioner oberoende av steglängden:
- Om \( f(x) \; = \; x^2 + b\,x + c \) då gäller
- \[ {f(x + h) \, - \, f(x-h) \over 2\,h} \; = \; 2\,x + b \; = \; f\,'(x) \]
Bevis:
Vi tillämpar den centrala differenskvoten på \( \, f(x) = x^2 + b\,x + c \, \):
\[ \begin{array}{rcl} f(x + h) & = & (x+h)^2 + b\,(x+h) + c = x^2 + 2\,x\,h + h^2 + b\,x + b\,h + c \\ f(x - h) & = & (x-h)^2 + b\,(x-h) + c = x^2 - 2\,x\,h + h^2 + b\,x - b\,h + c \\ f(x+h) - f(x-h) & = & x^2 + 2\,x\,h + h^2 + b\,x + b\,h + c - (x^2 - 2\,x\,h + h^2 + b\,x - b\,h + c) = 4\,x\,h + 2\,b\,h = 2\,h\,(2\,x + b) \\ \displaystyle {f(x + h) - f(x-h) \over 2\,h} & = & \displaystyle {{\color{Red} {2\,h}}\,(2\,x + b) \over {\color{Red} {2\,h}}} = 2\,x + b = f\,'(x) \\ \end{array}\] Att resultatet är oberoende av steglängden visas i beviset ovan genom att \( h\, \) förkortas bort och inte längre förekommer i slutresultatet \( \, 2\,x + b \, \).
När ska man använda numerisk derivering?
I följande situationer är det nödvändigt resp. rimligt att använda numerisk derivering:
Fall 1: Funktioner som inte matchar mot någon funktionstyp bland våra deriveringsregler. Exempel:
- a) \( \qquad\qquad\qquad \displaystyle f(x) \; = \; {1 \over x + 1} \)
- Denna funktion matchar inte mot någon funktionstyp i vår tabell över deriveringsregler, därför att \( \, f(x) \, \) inte kan skrivas om till en potens med basen \( \, x \), vilket vi t.ex. kunde göra med \( y = \displaystyle {1 \over x} \) genom att skriva om den till \( y = \, x^{-1} \). Sedan kunde vi använda deriveringsregeln för derivatan av en potens på den omskrivna formen \( y = \, x^{-1} \). Eftersom en sådan omskrivning inte går att göra med funktionen \( f(x) = \displaystyle {1 \over x + 1}\, \) kan den inte deriveras med denna regel. Inte heller med någon annan av de deriveringsregler vi känner till hittills. Det är nämnaren \(\, x + 1 \) som gör att uttrycket inte kan skrivas om till en potens med basen \( \, x \). Visserligen går det att skriva om så här: \( \, f(x) = \displaystyle {1 \over x + 1} = (x + 1)^{-1} \), men basen här är inte \( \, x \) utan \( \, x + 1 \).
- Funktionen i fråga kan anses som en kvot av två funktioner, nämligen \( \, 1 \, \) och \( \, x + 1 \). En deriveringsregel för en kvot av funktioner, den s.k. Kvotregeln som skulle kunna användas här, kommer vi att lära oss först i Matte 4-kursen.
- b) \( \qquad\qquad\qquad \displaystyle f(x) \; = \; {1 \over e^x + 1} \qquad\qquad\;\; \) Även denna funktion skulle endast kunna deriveras med Kvotregeln av samma anledning som a).
- c) \( \qquad\qquad\qquad f(x) \; = \; \ln x \qquad\qquad\qquad \) Därför deriverade vi den numeriskt med bakåtdifferenskvoten.
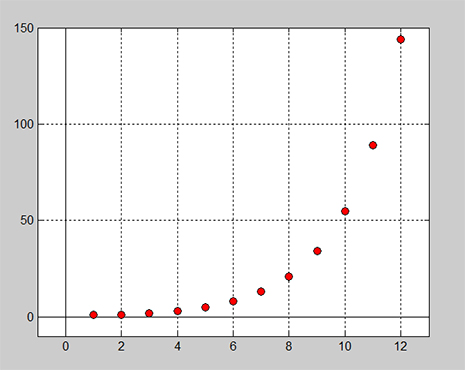
Fall 2: Diskreta funktioner som är givna i tabellform, t.ex. fibonaccitalen som behandlades i kap 1, där de \( \, 12 \, \) första fibonaccitalen beräknades:
|
Med denna värdetabell kan vi rita grafen
till höger som illustrerar fibonaccitalens snabba tillväxt. Den horisontella axeln visar antal månader och den vertikala antal kaninpar.
Fibonaccitalen bildar en diskret funktion, därför att dess defini- tionsmängd är heltalen \( \, {\color{Red} 1}\)-\({\color{Red} {12}}\). |
 |
- Som man ser ökar kaninpopulationen ganska fort. Men hur snabbt ökar den? Kan man derivera en diskret funktion vars tabell har en minsta steglängd?
- Svaret är: ja, men endast numeriskt:
Exempel på en diskret funktions derivata i en punkt
Fibonaccis funktion är given i tabellen ovan med:
- \[ n \, = \, {\rm Antalet\;månader} \]
- \[ F(n)\, = \, {\rm Antalet\;kaninpar\;i\;månaden} \, n \]
Hur snabbt ökar kaninpopulationen i månaden \( \, 11 \, \)? Dvs:
Beräkna \( \, F\,'(11) \, \) så noggrant som möjligt.
Lösning:
Vi väljer den centrala differenskvoten samt tabellens minsta steglängd \( \, h = 1 \).
\[ F\,'(11) \, \approx \, {F(11 + 1) - F(11 - 1) \over 2\cdot 1} \, = \, {F(12) - F(10) \over 2} \, = \, {144 - 55 \over 2} \, = \, 44,5 \]
Dvs kaninerna fortplantar sig i den \( \, 11\)-te månaden med minst \( \, 44 \, \) kaninpar per månad.
Fall 3: Funktionens derivata blir så komplicerad att det tar mer tid att ställa upp den (och risken för felräkning ökar) än att derivera den numeriskt.
- Exempel: \( \qquad \displaystyle f(x) = {\sin\,3\,x \over 4\,\cos\,x} \qquad\Longrightarrow\qquad f\,'(x) = {12\,\cos\,3\,x \cdot \cos\,x \,+\, 4\,\sin\,3\,x \cdot \sin\,x \over 16\,\cos^2\,x} \)
- För det första är det inte enkelt att ställa upp \( f\,'(x) \). Även här skulle Kvotregeln behövas samt deriveringsreglerna för sinus- och cosinusfunktioner.
- För det andra ser man att det är väsentligt enklare att beräkna t.ex. \( f(2)\, \) än \( f\,'(2) \). I de numeriska deriveringsformlerna ingår nämligen endast beräkningar av \( f(x)\, \), inte av \( f\,'(x) \).
Copyright © 2011-2018 Taifun Alishenas. All Rights Reserved.
