Skillnad mellan versioner av "3.2 Lokala maxima och minima"
Taifun (Diskussion | bidrag) m (→Lösning med teckentabell:) |
Taifun (Diskussion | bidrag) m (→Lösning med teckentabell:) |
||
| Rad 259: | Rad 259: | ||
<td><math>2</math></td> | <td><math>2</math></td> | ||
<td>2,1</td> | <td>2,1</td> | ||
| − | <td> | + | <td>3,9</td> |
| − | <td><math> | + | <td><math>4</math></td> |
| − | <td> | + | <td>4,1</td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| Rad 268: | Rad 268: | ||
<td><math>0</math></td> | <td><math>0</math></td> | ||
<td><math>+</math></td> | <td><math>+</math></td> | ||
| − | |||
| − | |||
<td><math>+</math></td> | <td><math>+</math></td> | ||
| + | <td><math>0</math></td> | ||
| + | <td><math>-</math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| Rad 277: | Rad 277: | ||
<td> <strong><span style="color:red">Min</span></strong> </td> | <td> <strong><span style="color:red">Min</span></strong> </td> | ||
<td> <strong><big><big>↗</big></big></strong> </td> | <td> <strong><big><big>↗</big></big></strong> </td> | ||
| − | |||
| − | |||
<td> <strong><big><big>↗</big></big></strong> </td> | <td> <strong><big><big>↗</big></big></strong> </td> | ||
| + | <td> <strong><span style="color:red">Min</span></strong> </td> | ||
| + | <td> <strong><big><big>↘</big></big></strong> </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Versionen från 22 november 2014 kl. 12.15
| <-- Förra avsnitt | Teori | Övningar | --> Nästa avsnitt |
Innehåll
Regel om maxima och minima med andraderivata
:
Derivatans nollställen och andraderivatans förtecken avgör för vilka \(\, x \) en funktion har maxima och minima:
Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett maximum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och andraderivatan \( {\color{White} x} f\,''(a) \, {\bf {\color{Red} <}} \, 0 {\color{White} x}. \)
Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett minimum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och andraderivatan \( {\color{White} x} f\,''(a) \, {\bf {\color{Red} >}} \, 0 {\color{White} x}. \)
Med andraderivatan menas derivatans derivata som betecknas med \( f\,''(x) \) och läses \( {\rm "}f \; {\rm biss\;av\; } x\,{\rm "}\). Man får andraderivatan genom att derivera derivatans funktion en gång till.
Med derivatan menas alltid första derivatan. Med maximum menas en funktions största och med minimum en funktions minsta värde.
| Regeln ovan säger i ord:
|
Där derivatan är \( \, 0 \) och andraderivatan är negativ har funktionen ett maximum.
Där derivatan är \( \, 0 \) och andraderivatan är positiv har funktionen ett minimum. |
I exemplet nedan behandlas en funktion vars graf visar ett minimum. En algebraisk metod används för att med hjälp av regeln ovan hitta detta minimum dvs bestämma det \(\, x \) för vilket funktionen antar sitt minimum. Med detta \(\, x \) beräknas sedan funktionens minsta värde.
Exempel 1 Vinternattens kallaste tidpunkt
Vi återgår till Exempel 1 i förra avsnitt, men byter frågeställning: Vi tittar inte längre på funktionens växande eller avtagande utan på funktionens minsta värde (minimum):
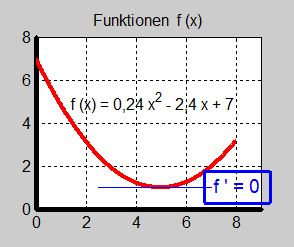
Under en vinternatt varierar temperaturen enligt funktionen \( {\color{White} x} \; y \, = \, f(x) \, = \, 0,24\,x^2\,-\,2,4\,x\,+\,7 {\color{White} x} \; \) med definitionsområdet: \( \quad 0 \leq x \leq 8 \).
där \( y \; = \) temperaturen i grader Celsius och
\( x \; = \) tiden i timmar efter midnatt
a) Ställ upp första- och andraderivatan. Rita graferna till \( \,f(x) \), \( \,f'(x) \) och \( \,f''(x) \) i separata koordinatsystem.
b) Bestäm nattens kallaste tidpunkt algebraiskt.
c) Bestäm nattens lägsta temperatur algebraiskt.
Lösning:
a) \( f(x) \, = \, 0,24\,x^2 - 2,4\,x + 7 \)
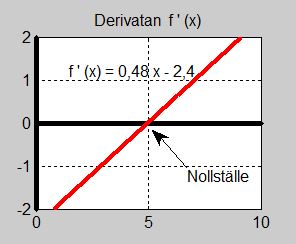
- \[ f'(x) \, = \, 0,48\,x - 2,4 \]
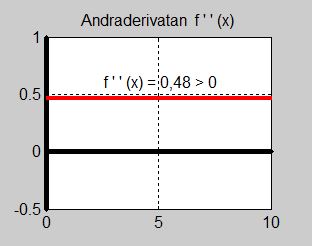
- \[ f''(x) \, = \, 0,48 \]
b) För att få reda på derivatans nollställe som regeln om maxima och minima med andraderivata kräver sätter vi derivatan till \( \, 0 \) och beräknar tidpunkten \( x \, \) då derivatan blir \( \, 0 \):
- \[\begin{array}{rcrcl} f'(x) & = & 0,48\,x - 2,4 & = & 0 \\ & & 0,48\,x & = & 2,4 \\ & & x & = & {2,4 \over 0,48} \\ & & x & = & 5 \end{array}\]
Nu vet vi att derivatan blir \( \, 0 \) i \( x = 5 \, \) dvs tangenten till kurvan \( y = f(x) \, \) är horisontell i \( x = 5 \, \). Men en horisontell tangent kan vara ett maximum eller ett minimum.
För att avgöra om det föreligger ett maximum eller ett minimum kräver regeln andraderivatans förtecken. Därför sätter vi \( x = 5 \, \) in i andraderivatan och kollar om den blir positiv eller negativ:
- \[ f''(5) = 0,48 \,>\, 0 \]
Andraderivatan är positiv (konstant) för alla \( x \, \) och därmed även för \( x = 5 \, \). Därav följer att \( f(x) \, \) har ett minimum i \( x = 5 \, \).
Alltså är nattens kallaste tidpunkt kl \( 5 \, \).
c) Temperaturen vid kl \( 5 \, \) är:
- \[ f(5) = 0,24 \cdot 5^2 - 2,4 \cdot 5 + 7 = 1 \]
Alltså är nattens lägsta temperatur \( 1 \, \) grad Celsius.
Regel om maxima och minima med teckentabell
:
Derivatans nollställen och dess teckenbyte kring nollställena avgör för vilka \(\, x \) en funktion har maxima och minima:
Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett maximum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och derivatan byter förtecken från \( {\color{White} x} + {\color{White} x} \) till \( {\color{White} x} - {\color{White} x} \) kring \( \, a \).
Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett minimum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och derivatan byter förtecken från \( {\color{White} x} - {\color{White} x} \) till \( {\color{White} x} + {\color{White} x} \) kring \( \, a \).
Med kring \( \, a \) menas i en tillräckligt liten omgivning av \( \, a \), vilket i sin tur betyder att man ska undersöka teckenbytet i en omgivning som är så nära som möjligt nollstället \( \, x=a \).
Vi tar samma exempel som ovan: Exempel 1 Vinternattens kallaste tidpunkt, bibehåller frågeställning, men byter metod: Vi bestämmer fortfarande derivatans nollställen, men använder inte längre andraderivatan utan regeln ovan för att med hjälp av en teckentabell skilja mellan maximum och minimum. Där hade vi redan bestämt att derivatan var \( \, 0 \) för \( \, x = 5 \). För säkerhets skull kontrollerar vi detta:
- \[ f'(x) = 0,48\,x - 2,4 \]
- \[ f' (5) = 0,48\cdot 5 - 2,4 = 0 \]
Nu ska vi undersöka derivatans förtecken till vänster och till höger om nollstället \( \, x = 5 \). Vi väljer t.ex. punkterna \( \, x = 4,9 \) och \( \, x = 5,1 \) på x-axeln som är ganska nära derivatans nollställe och bestämmer derivatans förtecken i dessa punkter:
- \[ f' (4,9) = 0,48\cdot 4,9 - 2,4 = - 0,048 < 0 \]
- \[ f' (5,1) = 0,48\cdot 5,1 - 2,4 = 0,048 > 0 \]
För översiktlighetens skull skriver vi in våra resultat i följande teckentabell:
| \(x\) | 4,9 | \(5\) | 5,1 |
| \( f\,'(x) \) | \(-\) | \(0\) | \(+\) |
| \( \,f(x) \) | ↘ | Min | ↗ |
Samtidigt tillämpar vi regeln om maxima och minima med teckentabell och drar av den slutsatsen att funktionen \( f(x)\, \) har ett minimum i \( \, x = 5 \), därför att \( f\,'(5) = 0 \) och derivatan byter förtecken från \(-\) till \( + \) kring \( \, 5 \) när vi rör oss framåt på \(\,x\)-axeln. Även denna slutsats finns med i teckentabellen.
Dessutom har vi för tydlighetens skull använt oss av ↘ och ↗ för att illustrera att \( f(x)\, \) är avtagande till vänster om och växande till höger om \( \, 5 \) vilket åskådliggör att det föreligger ett minimum i \( \, x = 5 \).
Exempel 2 Maximal företagsvinst
Vi återgår till Exempel 3 i förra avsnitt, men byter frågeställning: Vi frågar inte längre under vilka perioder företagets vinst växer eller avtar utan när företaget uppnår maximal vinst och hur stor denna vinst blir. Dvs vi vill nu bestämma vinstfunktionens maximum.
Efter statistiska observationer har man kommit fram till att ett företags vinst kan beräknas enligt funktionen:
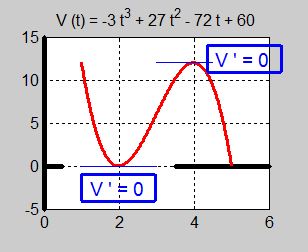
- \[ V(t) \; = \; -3\,t^3\,+\,27\,t^2\,-\,72\,t\,+\,60 \]
där \( V \; = \) företagets vinst i \( 1\,000 \) kr och
\( t \;\, = \) tiden i antalet år efter årsskiftet 2009/2010 \(. \qquad \) Definitionsområde: \( \; 1 \leq t \leq 5 \)
a) Ställ upp första- och andraderivatan. Rita graferna till \( \,V(t) \), \( \,V'(t) \) och \( \,V''(t) \) i separata koordinatsystem.
b) När har företaget maximal vinst?
c) Hur stor är företagets maximala vinst?
Frågorna b) och c) ska besvaras algebraiskt. Dessutom ska b) lösas både med andraderivatan och teckentabellen.
Lösning:
a) \( V(t) \, = \, -3\,t^3 + 27\,t^2 - 72\,t + 60 \)
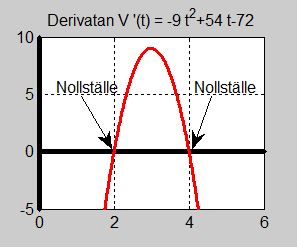
- \[ V'(t) \, = \, -9\,t^2 + 54\,t - 72 \]
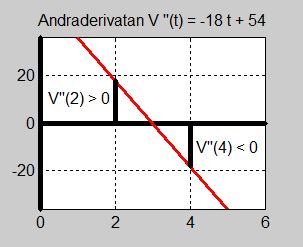
- \[ V''(t) \, = \, -18\,t + 54 \]
b) Derivatan är en 2:a gradsfunktion och har två reella nollställen. För att få reda på dem sätter vi derivatan till \( \, 0 \):
- \[\begin{array}{rcrcl} V'(t) & = & -9\,t^2 + 54\,t - 72 & = & 0 \\ & & t^2 - 6 \,t + 8 & = & 0 \end{array}\]
- 2:a gradsekvationen kan enkelt och snabbt lösas med Vieta:
- \[ \begin{array}{rcl} t_1 + t_2 & = & -(-6) = 6 \\ t_1 \cdot t_2 & = & 8 \\ &\Downarrow& \\ t_1 & = & 2 \\ t_2 & = & 4 \end{array}\]
- Derivatan blir alltså \( \, 0 \) i \( t_1 = 2 \, \) och \( t_2 = 4 \, \). Dvs tangenten till vinstfunktionen \( \, V(t)\):s graf är horisontell i dessa två punkter. En horisontell tangent kan innebära ett maximum eller ett minimum.
- För att avgöra var det finns ett maximum och var ett minimum tillämpar vi regeln om maxima och minima med andraderivata:
- Lösning med andraderivata:
- Regeln som kräver andraderivatans förtecken tillämpas på vart och ett nollställe enskilt.
- Nollställe 1: \( {\color{White} x} t_1 = 2 \quad {\color{White} x} \)
- Vi sätter in \( t_1 = 2 \, \) i andraderivatan och kollar om den blir positiv eller negativ:
- \[ V''(t) \, = \, -18\,t + 54 \]
- \[ V''(2) \, = \, -18\cdot 2 + 54 = 18 > 0 \]
- Andraderivatan är positiv för \( t_1 = 2 \, \). Slutsats: \( V(t) \, \) har ett minimum i \( t_1 = 2 \, \).
- Nollställe 2: \( {\color{White} x} t_2 = 4 \quad {\color{White} x} \)
- Vi sätter in \( t_2 = 4 \, \) in i andraderivatan och kollar om den blir positiv eller negativ:
- \[ V''(4) \, = \, -18\cdot 4 + 54 = -18 < 0 \]
- Andraderivatan är negativ för \( t_2 = 4 \, \). Slutsats: \( V(t) \, \) har ett maximum i \( t_2 = 4 \, \).
- Alltså har företaget sin största vinst efter \( t_2 = 4 \, \) år efter årsskiftet 2009/2010, dvs vid årsskiftet 2013/2014.
Lösning med teckentabell:
- Alternativt använder vi här regeln om maxima och minima med teckentabell för att skilja mellan maximum och minimum.
- Regeln kräver derivatans teckenbyte i en nära omgivning av derivatans nollställen. Vi tillämpar regeln på vart och ett nollställe enskilt.
- Nollställe 1: \( {\color{White} x} t_1 = 2 \)
- Vi väljer t.ex. punkterna \( \, t = 1,9 \) och \( \, t = 2,1 \) på t-axeln som är ganska nära derivatans nollställe 1 och bestämmer derivatans förtecken i dessa punkter:
- \[ V'(t) = -9\,t^2 + 54\,t - 72 \]
- \[ V' (1,9) = -9\cdot 1,9^2 + 54\cdot 1,9 - 72 = -1,89 < 0 \]
- \[ V' (2,1) = -9\cdot 2,1^2 + 54\cdot 2,1 - 72 = 1,71 > 0 \]
- Nollställe 2: \( {\color{White} x} t_2 = 4 \)
- Vi väljer t.ex. punkterna \( \, t = 3,9 \) och \( \, t = 4,1 \) på t-axeln nära \( t_2 \) och bestämmer derivatans förtecken i dessa punkter:
- \[ V' (3,9) = -9\cdot 3,9^2 + 54\cdot 3,9 - 72 = 1,71 > 0 \]
- \[ V' (4,1) = -9\cdot 4,1^2 + 54\cdot 4,1 - 72 = -1,89 < 0 \]
Alla dessa resultat skrivs in i följande teckentabell:
| \(x\) | 1,9 | \(2\) | 2,1 | 3,9 | \(4\) | 4,1 |
| \( f\,'(x) \) | \(-\) | \(0\) | \(+\) | \(+\) | \(0\) | \(-\) |
| \( \,f(x) \) | ↘ | Min | ↗ | ↗ | Min | ↘ |
Samtidigt tillämpar vi regeln om maxima och minima med teckentabell och drar av den slutsatsen att funktionen \( f(x)\, \) har ett minimum i \( \, x = 5 \), därför att \( f\,'(5) = 0 \) och derivatan byter förtecken från \(-\) till \( + \) kring \( \, 5 \) när vi rör oss framåt på \(\,x\)-axeln. Även denna slutsats finns med i teckentabellen.
Dessutom har vi för tydlighetens skull använt oss av ↘ och ↗ för att illustrera att \( f(x)\, \) är avtagande till vänster om och växande till höger om \( \, 5 \) vilket åskådliggör att det föreligger ett minimum i \( \, x = 5 \).
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.