Skillnad mellan versioner av "3.3 Terasspunkter"

Från Mathonline
Hoppa till: navigering, sök
m
m
Rad 18: Rad 18:
 
== Terasspunkter ==
 
== Terasspunkter ==
  
−
I förra avsnitt lärde vi oss två metoder för att hitta en extrempunkt dvs ett maximum eller ett minimum:
+
I förra avsnitt lärde vi oss två metoder för att hitta en funktions extrempunkter dvs ett maxima eller ett minima:
  
−
* f
+
* Med andraderivata: Funktionens derivata <math> \, = \, 0 \, </math> och andraderivatan <math> \, < \, 0 \, </math> eller <math> \, > \, 0 \, </math> dvs <math> \, \neq \, 0 \, </math>.
  
−
* g
+
* Med teckenstudium: Funktionens derivata <math> \, = \, 0 \, </math> och derivatan byter tecken kring sitt nollställe.
  
−
, om derivatan är <math>\,0\,</math> och byter tecken +++
+
Båda metoder uteslöt följande alternativ:
  
−
Under en vinternatt varierar temperaturen enligt funktionen <math> {\color{White} x} \; y \, = \, f(x) \, = \, 0,24\,x^2\,-\,2,4\,x\,+\,7 {\color{White} x} \; </math> med definitionsområdet<span style="color:black">:</span> <math> \quad 0 \leq x \leq 8 </math>.
+
* Med andraderivata: Både funktionens derivata och andraderivata <math> \, = \, 0 \, </math>.
  
−
där &nbsp;&nbsp; <math> y \; = </math> &nbsp; temperaturen i grader Celsius och
+
* Med teckenstudium: Funktionens derivata <math> \, = \, 0 \, </math> och derivatan byter inte tecken kring sitt nollställe, utan behåller sitt tecken.
  
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; <math> x \; = </math> &nbsp; tiden i timmar efter midnatt
+
Detta alternativ tar vi upp nu: Vad händer om funktionens derivata och andraderivata <math> \, = \, 0 \, </math> eller om funktionens derivata <math> \, = \, 0 \, </math> och behåller sitt tecken kring sitt nollställe?
  
−
a) &nbsp; Ställ upp första- och andraderivatan. Rita graferna till <math> \,f(x) </math>, <math> \,f'(x) </math> och <math> \,f''(x) </math> i separata koordinatsystem.
+
Ett sådant fall föreligger i följande enkelt exempel:
  
−
b) &nbsp; Bestäm nattens kallaste tidpunkt algebraiskt.
+
:::<math> f(x) \, = \, x^3 </math>
  
−
c) &nbsp; Bestäm nattens lägsta temperatur algebraiskt.
+
::<math> f'(x) \, = \, 3\,x^2 </math>
−
----
+
  
−
 
+
::<math> f''(x) \, = \, 6\,x </math>
−
'''Lösning:'''
+
−
 
+
−
a) &nbsp; <math> f(x) \, = \, 0,24\,x^2 - 2,4\,x + 7 </math>
+
−
 
+
−
::<math> f'(x) \, = \, 0,48\,x - 2,4 </math>
+
−
 
+
−
::<math> f''(x) \, = \, 0,48 </math>
+
  
 
[[Image: Terasspunkt 1.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Terasspunkt 2.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Terasspunkt 3.jpg]]
 
[[Image: Terasspunkt 1.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Terasspunkt 2.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Terasspunkt 3.jpg]]
−
----
 
−
 
−
 
−
b) &nbsp; För att få reda på derivatans nollställe som [[3.2_Maxima_och_minima#Regler_om_maxima_och_minima_med_andraderivata|<strong><span style="color:blue">reglerna om maxima och minima med andraderivata</span></strong>]] kräver sätter vi derivatan till <math> \, 0 </math> och beräknar den tidpunkt <math> x \, </math> då derivatan blir <math> \, 0 </math>:
 
−
 
−
::<math>\begin{array}{rcrcl}  f'(x) & = & 0,48\,x - 2,4 & = & 0  \\
 
−
                                    &  & 0,48\,x      & = & 2,4 \\
 
−
                                    &  &      x      & = & {2,4 \over 0,48} \\
 
−
                                    &  &      x      & = & 5
 
−
  \end{array}</math>
 
−
 
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Nu vet vi att derivatan blir <math> \, 0 </math> i <math> x = 5 \, </math> dvs tangenten till kurvan <math> y = f(x) \, </math> har lutningen <math> 0\, </math> dvs är horisontell i <math> x = 5 \, </math>.
 
−
 
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Därmed är det bevisat att <math> \, x = 5 \, </math> är en extrempunkt. Men en extrempunkt kan vara ett maximum eller ett minimum.
 
−
 
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; För att avgöra om denna extrempunkt är ett maximum eller ett minimum kräver regeln andraderivatans tecken.
 
−
 
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Därför sätter vi <math> x = 5 \, </math> in i andraderivatan och kollar om den blir positiv eller negativ:
 
−
 
−
:::::<math> f''(5) = 0,48 \,>\, 0 </math>
 
−
 
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Andraderivatan är positiv (konstant) för alla <math> x \, </math> och därmed även för <math> x = 5 \, </math>. Därav följer att <math> f(x) \, </math> har ett minimum i <math> x_{min} = 5 \, </math>.
 
−
 
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Alltså är nattens kallaste tidpunkt kl <math> 5 \, </math>.
 
−
----
 
−
 
  
−
c) &nbsp; Temperaturen vid kl <math> 5 \, </math> är:
 
  
−
::<math> f(x_{min}) = f(5) = 0,24 \cdot 5^2 - 2,4 \cdot 5 + 7  = 1 </math>
+
+++ För att få reda på +++
  
−
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Alltså är nattens lägsta temperatur <math> 1 \, </math> grad Celsius.
 
  
 
== Regeln om terasspunkter ==
 
== Regeln om terasspunkter ==

Versionen från 27 december 2014 kl. 23.41

       <-- Förra avsnitt          Teori          Övningar          --> Nästa avsnitt      


Lektion 31 Kurvkonstruktion med derivata I

Lektion 32 Kurvkonstruktion med derivata II


Terasspunkter

I förra avsnitt lärde vi oss två metoder för att hitta en funktions extrempunkter dvs ett maxima eller ett minima:

  • Med andraderivata: Funktionens derivata \( \, = \, 0 \, \) och andraderivatan \( \, < \, 0 \, \) eller \( \, > \, 0 \, \) dvs \( \, \neq \, 0 \, \).
  • Med teckenstudium: Funktionens derivata \( \, = \, 0 \, \) och derivatan byter tecken kring sitt nollställe.

Båda metoder uteslöt följande alternativ:

  • Med andraderivata: Både funktionens derivata och andraderivata \( \, = \, 0 \, \).
  • Med teckenstudium: Funktionens derivata \( \, = \, 0 \, \) och derivatan byter inte tecken kring sitt nollställe, utan behåller sitt tecken.

Detta alternativ tar vi upp nu: Vad händer om funktionens derivata och andraderivata \( \, = \, 0 \, \) eller om funktionens derivata \( \, = \, 0 \, \) och behåller sitt tecken kring sitt nollställe?

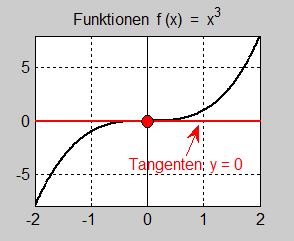
Ett sådant fall föreligger i följande enkelt exempel:

\[ f(x) \, = \, x^3 \]
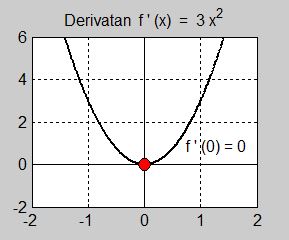
\[ f'(x) \, = \, 3\,x^2 \]
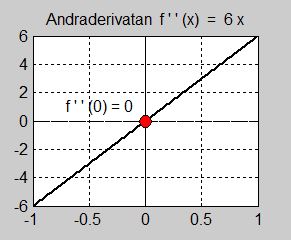
\[ f''(x) \, = \, 6\,x \]

Terasspunkt 1.jpg      Terasspunkt 2.jpg      Terasspunkt 3.jpg


+++ För att få reda på +++


Regeln om terasspunkter

Två kriterier behövs för att få reda på en funktions maxima och minima: ett om derivatans nollställen, ett om andraderivatans tecken. Båda måste vara uppfyllda. Följande regler gäller:

:

Derivatans nollställen och andraderivatans tecken avgör för vilka \(\, x \) en funktion har maxima resp. minima:


Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett maximum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och andraderivatan \( {\color{White} x} f\,''(a) \, {\bf {\color{Red} <}} \, 0 {\color{White} x}. \)

Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett minimum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och andraderivatan \( {\color{White} x} f\,''(a) \, {\bf {\color{Red} >}} \, 0 {\color{White} x}. \)

Om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och andraderivatan \( {\color{White} x} f\,''(a) \, {\bf {\color{Red} =}} \, 0 {\color{White} x} \) har funktionen varken ett maximum eller ett minimum.


Reglerna ovan säger i ord:



Där derivatan är \( \, 0 \) och andraderivatan är negativ har funktionen ett maximum.

Där derivatan är \( \, 0 \) och andraderivatan är positiv har funktionen ett minimum.

Där både derivatan och andraderivatan är \( \, 0 \) föreligger varken ett maximum eller ett minimum. Vad som gäller då behandlas i nästa avsnitt.


Ingen terasspunkt

Globala maxima och minima

Exempel på kurvkonstruktion

Ett lurigt fall

Hämtad från "https://matte3c.mathonline.se/index.php?title=3.3_Terasspunkter&oldid=19512"