Skillnad mellan versioner av "3.3 Övningar till Terasspunkter"
Från Mathonline
Taifun (Diskussion | bidrag) (Skapade sidan med '__NOTOC__ {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | style="border-bottom:1px solid #797979" width="5px" | {{Not selected tab|3.2 Lokala...') |
Taifun (Diskussion | bidrag) |
||
| Rad 14: | Rad 14: | ||
== Övning 1 == | == Övning 1 == | ||
| + | <div class="ovning"> | ||
| + | Följande funktion <math> \,y = f(x) </math> är definierad genom sin graf: | ||
| + | :[[Image: Ovn 1a.jpg]] | ||
| + | |||
| + | |||
| + | Använd grafen ovan för att besvara följande frågor: | ||
| + | |||
| + | a) För vilka <math> \,x </math> är funktionen växande? | ||
| + | |||
| + | b) För vilka <math> \,x </math> är funktionen avtagande? | ||
| + | |||
| + | c) Finns det <math> \,x</math>-värden för vilka funktionen varken är växande eller avtagande? I så fall ange dem. | ||
| + | |||
| + | d) För vilka <math> \,x </math> är funktionen <math> f(x) = 0 \, </math> ? | ||
| + | |||
| + | e) För vilka <math> \,x </math> är derivatan <math> \,f'(x) = 0 \, </math> ? | ||
| + | |||
| + | f) Vilka av frågorna ovan är olika formuleringar av samma fråga och har därför samma svar? | ||
| + | |||
| + | </div>{{#NAVCONTENT:Svar 1a|3.1 Svar 1a|Svar 1b|3.1 Svar 1b|Svar 1c|3.1 Svar 1c|Svar 1d|3.1 Svar 1d|Svar 1e|3.1 Svar 1e|Svar 1f|3.1 Svar 1f}} | ||
| + | |||
| + | == Övning 2 == | ||
Versionen från 30 december 2014 kl. 14.00
| <-- Förra avsnitt | Teori | Övningar | --> Nästa avsnitt |
E-övningar: 1-4
Övning 1
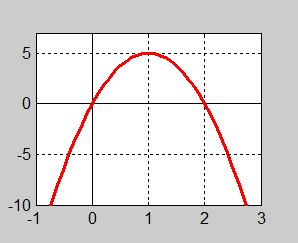
Följande funktion \( \,y = f(x) \) är definierad genom sin graf:
Använd grafen ovan för att besvara följande frågor:
a) För vilka \( \,x \) är funktionen växande?
b) För vilka \( \,x \) är funktionen avtagande?
c) Finns det \( \,x\)-värden för vilka funktionen varken är växande eller avtagande? I så fall ange dem.
d) För vilka \( \,x \) är funktionen \( f(x) = 0 \, \) ?
e) För vilka \( \,x \) är derivatan \( \,f'(x) = 0 \, \) ?
f) Vilka av frågorna ovan är olika formuleringar av samma fråga och har därför samma svar?
Svar 1a
Svar 1b
Svar 1c
Svar 1d
Svar 1e
Svar 1f
 Hämtar...
Hämtar...