Skillnad mellan versioner av "3.4 Kurvkonstruktioner"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 52: | Rad 52: | ||
</table> | </table> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Det finns två alternativa metoder att göra det, den ena använder [[3.2_Maxima_och_minima#Regler_om_maxima_och_minima_med_andraderivata|<strong><span style="color:blue">andraderivatan</span></strong>]], den andra genomför ett [[3.2_Maxima_och_minima#Regler_om_maxima_och_minima_med_teckenstudium|<strong><span style="color:blue">teckenstudium</span></strong>]]. Vi ställer upp regler och löser exempel för båda metoderna. | Det finns två alternativa metoder att göra det, den ena använder [[3.2_Maxima_och_minima#Regler_om_maxima_och_minima_med_andraderivata|<strong><span style="color:blue">andraderivatan</span></strong>]], den andra genomför ett [[3.2_Maxima_och_minima#Regler_om_maxima_och_minima_med_teckenstudium|<strong><span style="color:blue">teckenstudium</span></strong>]]. Vi ställer upp regler och löser exempel för båda metoderna. | ||
Versionen från 11 januari 2015 kl. 16.03
| <-- Förra avsnitt | Teori | Övningar | --> Nästa avsnitt |
Fortfarande förutsätts att alla funktioner \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) vi behandlar här är kontinuerliga i alla punkter av det betraktade området.
Globala maxima och minima
I detta avsnitt kommer vi att använda en funktions derivata som ett verktyg för att få information om själva funktionen, närmare bestämt om funktionens lokala maxima och minima.
 |
 |
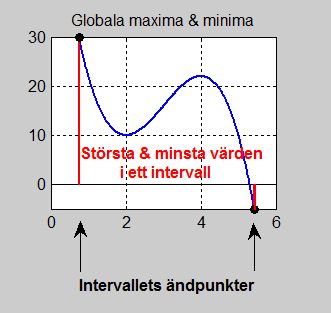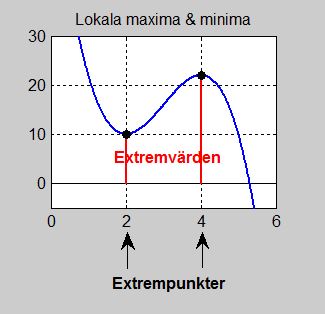Lokala maxima och minima är punkter (•) som har största resp. minsta \( \, y\)-värden lokalt dvs i sin närmaste omgivning, se bilden.
Med maxima och minima menas i detta avsnitt alltid lokala maxima/minima. Därför utelämnas ordet lokalt i detta avsnitt. Båda tillsammans heter extrema eller extremvärden. På bilden till vänster har vi två extremvärden: \( \, 10 \, \) och \( \, 22 \, \) (OBS! \( \, y\)-värden). De punkter på \( \, x\)-axeln för vilka extremvärden antas heter extrempunkter. På bilden finns två extrempunkter: \( \, 2 \, \) och \( \, 4 \, \) (OBS! \( \, x\)). Minimipunktens koordinater är: \( \, (2, 10) \, \). Maximipunktens koordinater är: \( \, (4, 22) \, \).
Tangenten till funktionens graf i en extrempunkt är horisontell dvs har lutningen \( \, 0 \, \). Följaktligen: Genom att bilda derivatan, sätta den till \( \, 0 \, \) och beräkna de \( \, x \, \) för vilka derivatan blir \( \, 0 \, \), kan vi få reda på funktionens extrempunkter.
|
Det finns två alternativa metoder att göra det, den ena använder andraderivatan, den andra genomför ett teckenstudium. Vi ställer upp regler och löser exempel för båda metoderna.
