Skillnad mellan versioner av "3.5 Övningar till Extremvärdesproblem"
Taifun (Diskussion | bidrag) m (→Övning 1) |
Taifun (Diskussion | bidrag) m |
||
| Rad 37: | Rad 37: | ||
</tr> | </tr> | ||
</table> | </table> | ||
| − | </div>{{#NAVCONTENT:Svar 1a|3. | + | </div>{{#NAVCONTENT:Svar 1a|3.5 Svar 1a|Svar 1b|3.5 Svar 1b|Lösning 1b|3.5 Lösning 1b|Svar 1c|3.5 Svar 1c|Lösning 1c|3.5 Lösning 1c|Svar 1d|3.5 Svar 1d|Lösning 1d|3.5 Lösning 1d}} |
== Övning 2 == | == Övning 2 == | ||
| Rad 72: | Rad 72: | ||
: Fyll i tabellen på de platser där det står ett frågetecken (?). | : Fyll i tabellen på de platser där det står ett frågetecken (?). | ||
| − | b) Lös övning 1a, men använd här en [[3. | + | b) Lös övning 1a, men använd här en [[3.5_Maxima_och_minima#Regler_om_maxima_och_minima_med_teckenstudium|<strong><span style="color:blue">teckentabell</span></strong>]] för att visa att du hittat maximipunkten. |
| − | </div>{{#NAVCONTENT:Svar 2a|3. | + | </div>{{#NAVCONTENT:Svar 2a|3.5 Svar 2a|Lösning 2b|3.5 Lösning 2b}} |
== Övning 3 == | == Övning 3 == | ||
| Rad 88: | Rad 88: | ||
a) När når kulan sin högsta höjd? | a) När når kulan sin högsta höjd? | ||
| − | : Bevisa med en av reglerna ([[3. | + | : Bevisa med en av reglerna ([[3.5_Maxima_och_minima#Regler_om_maxima_och_minima_med_andraderivata|<strong><span style="color:blue">andraderivatan</span></strong>]] eller [[3.5_Maxima_och_minima#Regler_om_maxima_och_minima_med_teckenstudium|<strong><span style="color:blue">teckentabell</span></strong>]]) att du hittat maximipunkten. |
b) Hur högt når kulan? | b) Hur högt når kulan? | ||
| − | </div>{{#NAVCONTENT:Svar 3a|3. | + | </div>{{#NAVCONTENT:Svar 3a|3.5 Svar 3a|Lösning 3a|3.5 Lösning 3a|Svar 3b|3.5 Svar 3b|Lösning 3b|3.5 Lösning 3b}} |
== Övning 4 == | == Övning 4 == | ||
| Rad 132: | Rad 132: | ||
: Ange maximi- och minimipunktens koordinater. | : Ange maximi- och minimipunktens koordinater. | ||
| − | </div>{{#NAVCONTENT:Svar 4a|3. | + | </div>{{#NAVCONTENT:Svar 4a|3.5 Svar 4a|Svar 4b|3.5 Svar 4b|Svar 4c|3.5 Svar 4c|Svar 4d|3.5 Svar 4d|Svar 4e|3.5 Svar 4e|Svar 4f|3.5 Svar 4f|Lösning 4f|3.5 Lösning 4f|Svar 4g|3.5 Svar 4g|Lösning 4g|3.5 Lösning 4g}} |
== Övning 5 == | == Övning 5 == | ||
| Rad 150: | Rad 150: | ||
: Vilket samband kan man konstatera mellan funktionens graf och derivatans graf? | : Vilket samband kan man konstatera mellan funktionens graf och derivatans graf? | ||
| − | </div>{{#NAVCONTENT:Svar 5a|3. | + | </div>{{#NAVCONTENT:Svar 5a|3.5 Svar 5a|Lösning 5a|3.5 Lösning 5a|Svar 5b|3.5 Svar 5b|Lösning 5b|3.5 Lösning 5b|Lösning 5c|3.5 Lösning 5c}} |
| Rad 170: | Rad 170: | ||
c) Rita en enkel skiss över funktionen <math> \, y = f(x)</math>. | c) Rita en enkel skiss över funktionen <math> \, y = f(x)</math>. | ||
| − | </div>{{#NAVCONTENT:Svar 6a|3. | + | </div>{{#NAVCONTENT:Svar 6a|3.5 Svar 6a|Svar 6b|3.5 Svar 6b|Lösning 6c|3.5 Lösning 6c}} |
== Övning 7 == | == Övning 7 == | ||
| Rad 182: | Rad 182: | ||
b) Sammanfatta dina resultat från a) i en teckentabell och rita en enkel skiss över funktionen <math> \, y = f(x)</math>. | b) Sammanfatta dina resultat från a) i en teckentabell och rita en enkel skiss över funktionen <math> \, y = f(x)</math>. | ||
| − | </div>{{#NAVCONTENT:Svar 7a|3. | + | </div>{{#NAVCONTENT:Svar 7a|3.5 Svar 7a|Lösning 7a|3.5 Lösning 7a|Lösning 7b|3.5 Lösning 7b}} |
== Övning 8 == | == Övning 8 == | ||
| Rad 193: | Rad 193: | ||
b) Rita graferna till funktionen <math> \, y = f(x) \, </math> och derivatan <math> \, y\,' = f\,'(x) \, </math> i två olika koordinatsystem. Markera funktionens maximi- resp. minimipunkter och derivatans nollställen. | b) Rita graferna till funktionen <math> \, y = f(x) \, </math> och derivatan <math> \, y\,' = f\,'(x) \, </math> i två olika koordinatsystem. Markera funktionens maximi- resp. minimipunkter och derivatans nollställen. | ||
| − | </div>{{#NAVCONTENT:Svar 8a|3. | + | </div>{{#NAVCONTENT:Svar 8a|3.5 Svar 8|Lösning 8a|3.5 Lösning 8|Lösning 8b|3.5 Lösning 8b}} |
| Rad 212: | Rad 212: | ||
Kontrollera om graferna visar de angivna extrema. | Kontrollera om graferna visar de angivna extrema. | ||
| − | </div>{{#NAVCONTENT:Svar 9a|3. | + | </div>{{#NAVCONTENT:Svar 9a|3.5 Svar 9a|Lösning 9a|3.5 Lösning 9a|Lösning 9b|3.5 Lösning 9b}} |
== Övning 10 == | == Övning 10 == | ||
| Rad 235: | Rad 235: | ||
c) Kontrollera dina resultat genom att rita graferna till funktionen <math> A(x) </math> och dess derivata i två olika koordinatsystem. | c) Kontrollera dina resultat genom att rita graferna till funktionen <math> A(x) </math> och dess derivata i två olika koordinatsystem. | ||
| − | </div>{{#NAVCONTENT:Svar 10a|3. | + | </div>{{#NAVCONTENT:Svar 10a|3.5 Svar 10a|Lösning 10a|3.5 Lösning 10a|Svar 10b|3.5 Svar 10b|Lösning 10b|3.5 Lösning 10b|Lösning 10c|3.5 Lösning 10c}} |
== Övning 11 == | == Övning 11 == | ||
| Rad 253: | Rad 253: | ||
c) Kontrollera om du får samma resultat som i övn. 10 när du i uttrycken här sätter in värdena <math> \, a = 20 \, </math> och <math> \, b = 30 \, </math> från övn. 10. | c) Kontrollera om du får samma resultat som i övn. 10 när du i uttrycken här sätter in värdena <math> \, a = 20 \, </math> och <math> \, b = 30 \, </math> från övn. 10. | ||
| − | </div>{{#NAVCONTENT:Svar 11a|3. | + | </div>{{#NAVCONTENT:Svar 11a|3.5 Svar 11a|Lösning 11a|3.5 Lösning 11a|Svar 11b|3.5 Svar 11b|Lösning 11b|3.5 Lösning 11b|Lösning 11c|3.5 Lösning 11c}} |
Versionen från 30 januari 2015 kl. 14.36
| <-- Förra avsnitt | Teori | Övningar |
E-övningar: 1-5
Övning 1
Övning 2
a) Följande teckentabell innehåller information om funktionen \(\, y = f(x)\):
| \(x\) | \(-1\) | \(0\) | |||
| \( f\,'(x) \) | \( - \) | \(0\) | \( + \) | \(0\) | \( - \) |
| \( f(x) \) | ↘ | ? | ↗ | ? | ↘ |
- Fyll i tabellen på de platser där det står ett frågetecken (?).
b) Lös övning 1a, men använd här en teckentabell för att visa att du hittat maximipunkten.
Övning 3
En kula skjuts rakt upp i luften och följer en bana som beskrivs av funktionen:
- \[ h(t) = - 4\,t^2 + 80\,t \]
där \( {\color{White} x} \; h\, = \, \) kulans höjd över marken i meter
\( {\color{White} {xxxx}} t\, = \, \) tiden efter kastet i sekunder
a) När når kulan sin högsta höjd?
- Bevisa med en av reglerna (andraderivatan eller teckentabell) att du hittat maximipunkten.
b) Hur högt når kulan?
Övning 4
Lös uppgifterna e)-g) algebraiskt:
e) Ställ upp derivatan \( \, f\,'(x)\, \).
f) Beräkna derivatan \( \, f\,'(x)\):s nollställen.
g) Använd en algebraisk metod för att skilja mellan maximi- och minimipunkten.
- Ange maximi- och minimipunktens koordinater.
Övning 5
Följande funktion är given:
- \[ f(x) \, = \, {x^4 \over 4} \, - \, 2\,x^2 \]
a) Ställ upp derivatan \( \, f\,'(x) \, \) och beräkna dess nollställen.
b) Avgör med någon av metoderna vi lärt oss, vilka av derivatans nollställen är funktionen \( \, f(x)\):s maxima resp. minima.
Ange alla maximi- och minimipunkter.
c) Rita graferna till funktionen \( \, y = f(x) \, \) och derivatan \( \, y\,' = f\,'(x) \, \) i två olika koordinatsystem.
- Vilket samband kan man konstatera mellan funktionens graf och derivatans graf?
C-övningar: 6-8
Övning 6
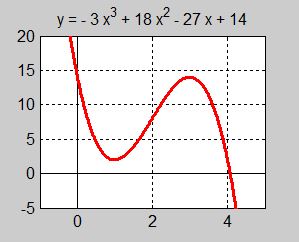
Följande är grafen till derivatan \( {\color{White} x} y' = f'(x) {\color{White} x} \) av en funktion \( \, y = f(x) \, \):
Besvara följande frågor om funktionen \( \, y = f(x) \, \) genom att använda information från derivatans graf (ovan):
a) Läs av från grafen och ange derivatans nollställe. Vad kan man säga om funktionen \( \, y = f(x) \, \) i derivatans nollställe?
b) Vilket teckenbyte har derivatan kring sitt nollställe? Vad följer av detta om funktionen?
c) Rita en enkel skiss över funktionen \( \, y = f(x)\).
Övning 7
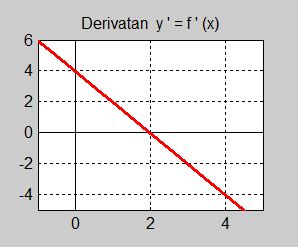
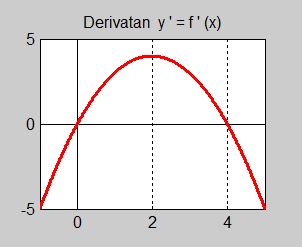
Följande är grafen till derivatan \( {\color{White} x} y' = f'(x) {\color{White} x} \) av en funktion \( \, y = f(x) \, \):
Lös följande uppgifter genom att endast använda grafen ovan:
a) Vilka slutsatser kan man dra om funktionen \( \, y = f(x) \, \) i derivatans nollställen? Motivera dina slutsatser.
b) Sammanfatta dina resultat från a) i en teckentabell och rita en enkel skiss över funktionen \( \, y = f(x)\).
Övning 8
Följande funktion är given:
- \[ y = f(x) = {(x - 1)\,(x^2 - 11\,x + 25) \over 3} \]
a) Beräkna koordinaterna till funktionens maximi- resp. minimipunkter exakt.
b) Rita graferna till funktionen \( \, y = f(x) \, \) och derivatan \( \, y\,' = f\,'(x) \, \) i två olika koordinatsystem. Markera funktionens maximi- resp. minimipunkter och derivatans nollställen.
A-övningar: 9-11
Övning 9
a) Bestäm konstanterna \( \, a, \, b \, \) och \( \, c \, \) så att funktionen
- \[ y = f(x) = a\,x^3 + b\,x^2 + c\,x \]
får ett maximum i punkten \( \, (-1, 7) \, \) och dessutom ett minimum för \( \, x = 2 \, \).
Ange funktionen \( \, y = f(x) \, \).
b) Rita graferna till funktionen \( \, y = f(x) \, \) och dess derivata i två olika koordinatsystem.
Kontrollera om graferna visar de angivna extrema.
Övning 10
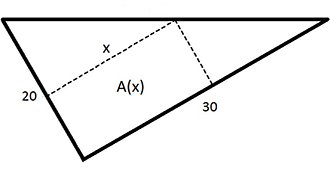
En tomt har formen av en rätvinklig triangel med följande mått i meter:
På tomten ska en rektangulär boyta väljas så att boytans area \( \, A(x) \, \) blir maximal.
a) Ställ upp ett uttryck för arean \( \, A(x) \, \) som endast beror av \( \, x \, \).
Tips: Kalla rektangelns andra sida för t.ex. \( \, y \,\). Ställ upp ett samband mellan \( \, y \,\) och \( \, x \, \).
Detta samband bestäms rektangelns "fria" hörn som är bunden till triangelns hypotenusa.
Inför ett koordinatsystem så att triangelns längre katet faller på \( x\)- och den kortare på \( y\)-axeln
och hypotenusan blir del av en rät linje vars ekvation ger det önskade sambandet.
b) Bestäm \( \, x \, \) så att funktionen \( \, A(x) \, \) antar sitt maximum och beräkna den maximala boytan.
c) Kontrollera dina resultat genom att rita graferna till funktionen \( A(x) \) och dess derivata i två olika koordinatsystem.
Övning 11
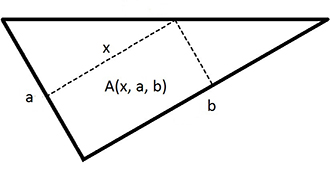
För att inte varje gång behöva räkna om övn. 10 för olika mått på tomter betraktas rätvinkliga trianglar av följande form:
där \( \, a \, \) och \( \, b \, \) är kateternas konstanta längder, dvs \( \, a > 0 \, \) och \( \, b > 0 \, \).
a) Ställ upp ett uttryck för arean \( \, A(x, a, b) \). Tips: se övn. 10.
Behandla i fortsättningen arean som en funktion \( \, A(x) \, \) av endast variabeln \( \, x \, \). Betrakta \( \, a, b\, \) som konstanter.
b) Bestäm \( \, x \, \) så att funktionen \( \, A(x) \, \) antar sitt maximum. Pga de obestämda konstanterna kommer \( \, x \, \) att vara ett uttryck i \( \, a \, \) resp. \( \, b \, \).
Ställ upp boytans maximala area som ett uttryck i \( \, a \, \) och \( \, b \, \)
c) Kontrollera om du får samma resultat som i övn. 10 när du i uttrycken här sätter in värdena \( \, a = 20 \, \) och \( \, b = 30 \, \) från övn. 10.
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.
 Hämtar...
Hämtar...