|
|
| Rad 164: |
Rad 164: |
| | <td>Du ska bygga en öppen låda av en kvadratisk kartong på <math> \, 10 \times 10 \; {\rm dm} \, </math>. | | <td>Du ska bygga en öppen låda av en kvadratisk kartong på <math> \, 10 \times 10 \; {\rm dm} \, </math>. |
| | | | |
| − | Det gör du genom att skära ut små kvadrater av längden <math> \, x \, </math> från kartongens | + | Det gör du genom att skära ut små kvadrater av längden <math> \, x \, </math> från karton- |
| | | | |
| − | fyra hörn enligt figuren. | + | gens fyra hörn enligt figuren. |
| | | | |
| − | Hur ska du välja <math> \, x \, </math> för att få den största möjliga volymen för din | + | Hur ska du välja <math> \, x \, </math> för att få den största möjliga volymen för din öppna |
| | | | |
| − | öppna låda?
| + | låda? |
| | | | |
| | | | |
Versionen från 31 januari 2015 kl. 18.18
E-övningar: 1-5
Övning 1
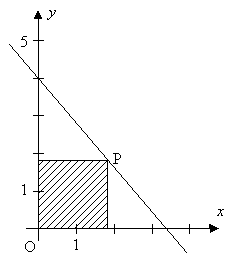
I figuren till höger rör sig punkten \( \, P \, \) på den räta linje vars ekvation är:
- \[ y = -\,{6 \over 5}\,x + 4 \]
Vilken position av \( \, P \, (x, \, y) \, \) ger maximal area till den skuggade rektangeln?
a) Vad är problemets bivillkor?
b) Ställ upp problemets målfunktion som en funktion av endast en variabel.
- Ange målfunktionens definitionsmängd.
c) Bestäm koordinaterna till punkten \( \, P \, \) så att rektangelns area blir maximal.
d) Beräkna rektangelns maximala area.
|
|
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Övning 2
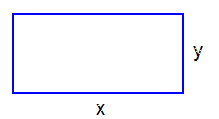
| En rektangel har omkretsen \( \, 12 \, {\rm cm} \, \). Maximera rektangelns area.
a) Formulera problemets bivillkor.
b) Ange problemets målfunktion samt definitionsmängd.
c) Bestäm sidorna \( \, x \, \) och \( \, y \, \) så att rektangelns area blir maximal.
d) Vad blir rektangelns maximala area?
|
|
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Övning 3
| En rektangels area är \( \, 25 \, {\rm cm}^2 \, \). Minimera rektangelns omkrets.
a) Formulera problemets bivillkor.
b) Ange problemets målfunktion samt definitionsmängd.
c) Bestäm sidorna \( \, x \, \) och \( \, y \, \) så att rektangelns omkrets blir minimal.
d) Vad blir rektangelns minimala omkrets?
|

|
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Övning 4
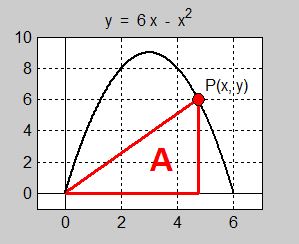
| En rätvinklig triangel är inbunden i en parabel enligt figuren:
Parabeln är definierad genom:
- \[ y \, = \, 6 \, x \, - \, x^2 \qquad {\rm med} \qquad 0 \, \leq \, x \, \leq \, 6 \]
Punkten \( \, P\,(x,\,y) \, \) rör sig på parabeln.
Vilken position av \( \, P \, \) ger triangeln största möjliga arean \( \, A \, \)?
a) Ange problemets bivillkor.
b) Ställ upp problemets målfunktion som en funktion \( \, A(x) \, \).
c) Bestäm \( \, x \, \) så att \( \, A(x) \, \) antar ett maximum.
d) Beräkna triangelns maximala area.
|
|
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Övning 5
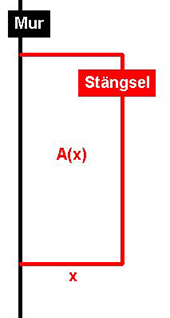
| En fårherde vill samla sina får under en sommarnatt vid en mur i ett inhägnat
rektangulärt område enligt figuren.
Han har en stängsel (rep eller dylikt) på \( \, 9 \; {\rm m} \, \) till förfogande.
Hur ska han välja rektangulära områdets mått för att få den största möjliga ytan
för sina får?
a) Ställ upp problemets målfunktion som en funktion \( \, A(x) \, \).
b) Ange målfunktionens definitionsmängd.
c) Bestäm \( \, x \, \) så att \( \, A(x) \, \) antar ett maximum.
d) Beräkna rektangelns maximala area.
e) Rita grafen till målfunktionen \( \, A(x) \, \).
f) Skulle en annan geometrisk figur än rektangeln ge större yta för fåren?
- Om ja, vilken? Kan du ange den nya figurens mått och beräkna dess area?
|
|
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
C-övningar: 6-8
Övning 6
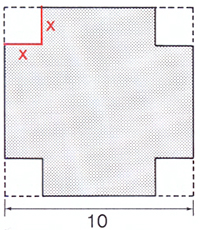
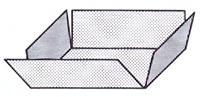
| Du ska bygga en öppen låda av en kvadratisk kartong på \( \, 10 \times 10 \; {\rm dm} \, \).
Det gör du genom att skära ut små kvadrater av längden \( \, x \, \) från karton-
gens fyra hörn enligt figuren.
Hur ska du välja \( \, x \, \) för att få den största möjliga volymen för din öppna
låda?
a) Ställ upp problemets målfunktion som en funktion \( \, A(x) \, \).
b) Ange målfunktionens definitionsmängd.
c) Bestäm \( \, x \, \) så att \( \, A(x) \, \) antar ett maximum.
d) Beräkna rektangelns maximala area.
e) Rita grafen till målfunktionen \( \, A(x) \, \).
f) Skulle en annan geometrisk figur än rektangeln ge större yta för fåren?
- Om ja, vilken? Kan du ange den nya figurens mått och beräkna dess area?
|
|
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Övning 7
Följande är grafen till derivatan \( {\color{White} x} y' = f'(x) {\color{White} x} \) av en funktion \( \, y = f(x) \, \):
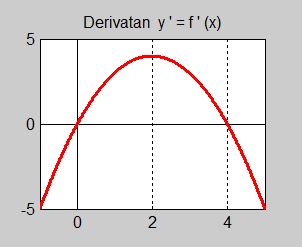
Lös följande uppgifter genom att endast använda grafen ovan:
a) Vilka slutsatser kan man dra om funktionen \( \, y = f(x) \, \) i derivatans nollställen? Motivera dina slutsatser.
b) Sammanfatta dina resultat från a) i en teckentabell och rita en enkel skiss över funktionen \( \, y = f(x)\).
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Övning 8
Följande funktion är given:
- \[ y = f(x) = {(x - 1)\,(x^2 - 11\,x + 25) \over 3} \]
a) Beräkna koordinaterna till funktionens maximi- resp. minimipunkter exakt.
b) Rita graferna till funktionen \( \, y = f(x) \, \) och derivatan \( \, y\,' = f\,'(x) \, \) i två olika koordinatsystem. Markera funktionens maximi- resp. minimipunkter och derivatans nollställen.
3.5 Svar 8
Hämtar...
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
A-övningar: 9-11
Övning 9
a) Bestäm konstanterna \( \, a, \, b \, \) och \( \, c \, \) så att funktionen
- \[ y = f(x) = a\,x^3 + b\,x^2 + c\,x \]
får ett maximum i punkten \( \, (-1, 7) \, \) och dessutom ett minimum för \( \, x = 2 \, \).
Ange funktionen \( \, y = f(x) \, \).
b) Rita graferna till funktionen \( \, y = f(x) \, \) och dess derivata i två olika koordinatsystem.
Kontrollera om graferna visar de angivna extrema.
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Övning 10
En tomt har formen av en rätvinklig triangel med följande mått i meter:
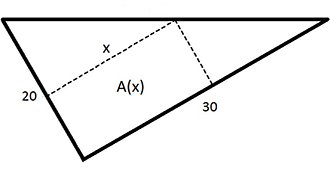
På tomten ska en rektangulär boyta väljas så att boytans area \( \, A(x) \, \) blir maximal.
a) Ställ upp ett uttryck för arean \( \, A(x) \, \) som endast beror av \( \, x \, \).
Tips: Kalla rektangelns andra sida för t.ex. \( \, y \,\). Ställ upp ett samband mellan \( \, y \,\) och \( \, x \, \).
Detta samband bestäms rektangelns "fria" hörn som är bunden till triangelns hypotenusa.
Inför ett koordinatsystem så att triangelns längre katet faller på \( x\)- och den kortare på \( y\)-axeln
och hypotenusan blir del av en rät linje vars ekvation ger det önskade sambandet.
b) Bestäm \( \, x \, \) så att funktionen \( \, A(x) \, \) antar sitt maximum och beräkna den maximala boytan.
c) Kontrollera dina resultat genom att rita graferna till funktionen \( A(x) \) och dess derivata i två olika koordinatsystem.
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Övning 11
För att inte varje gång behöva räkna om övn. 10 för olika mått på tomter betraktas rätvinkliga trianglar av följande form:
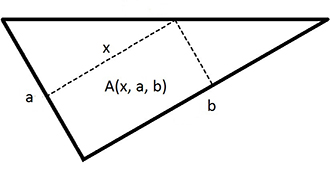
där \( \, a \, \) och \( \, b \, \) är kateternas konstanta längder, dvs \( \, a > 0 \, \) och \( \, b > 0 \, \).
a) Ställ upp ett uttryck för arean \( \, A(x, a, b) \). Tips: se övn. 10.
Behandla i fortsättningen arean som en funktion \( \, A(x) \, \) av endast variabeln \( \, x \, \). Betrakta \( \, a, b\, \) som konstanter.
b) Bestäm \( \, x \, \) så att funktionen \( \, A(x) \, \) antar sitt maximum. Pga de obestämda konstanterna kommer \( \, x \, \) att vara ett uttryck i \( \, a \, \) resp. \( \, b \, \).
Ställ upp boytans maximala area som ett uttryck i \( \, a \, \) och \( \, b \, \)
c) Kontrollera om du får samma resultat som i övn. 10 när du i uttrycken här sätter in värdena \( \, a = 20 \, \) och \( \, b = 30 \, \) från övn. 10.
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Visa mindre
Visa mer
Dölj allt
Visa allt
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.

 Hämtar...
Hämtar...






