Skillnad mellan versioner av "3.5 Övningar till Extremvärdesproblem"
Taifun (Diskussion | bidrag) m (→Övning 6) |
Taifun (Diskussion | bidrag) m |
||
| Rad 155: | Rad 155: | ||
| − | <Big><Big><Big><span style="color:blue">C-övningar: 6- | + | <Big><Big><Big><span style="color:blue">C-övningar: 6-7</span></Big></Big></Big> |
| Rad 207: | Rad 207: | ||
b) Sammanfatta dina resultat från a) i en teckentabell och rita en enkel skiss över funktionen <math> \, y = f(x)</math>. | b) Sammanfatta dina resultat från a) i en teckentabell och rita en enkel skiss över funktionen <math> \, y = f(x)</math>. | ||
</div>{{#NAVCONTENT:Svar 7a|3.5 Svar 7a|Lösning 7a|3.5 Lösning 7a|Lösning 7b|3.5 Lösning 7b}} | </div>{{#NAVCONTENT:Svar 7a|3.5 Svar 7a|Lösning 7a|3.5 Lösning 7a|Lösning 7b|3.5 Lösning 7b}} | ||
| + | |||
| + | |||
| + | <Big><Big><Big><span style="color:blue">A-övningar: 8-9</span></Big></Big></Big> | ||
| + | |||
== Övning 8 == | == Övning 8 == | ||
| Rad 218: | Rad 222: | ||
b) Rita graferna till funktionen <math> \, y = f(x) \, </math> och derivatan <math> \, y\,' = f\,'(x) \, </math> i två olika koordinatsystem. Markera funktionens maximi- resp. minimipunkter och derivatans nollställen. | b) Rita graferna till funktionen <math> \, y = f(x) \, </math> och derivatan <math> \, y\,' = f\,'(x) \, </math> i två olika koordinatsystem. Markera funktionens maximi- resp. minimipunkter och derivatans nollställen. | ||
</div>{{#NAVCONTENT:Svar 8a|3.5 Svar 8|Lösning 8a|3.5 Lösning 8|Lösning 8b|3.5 Lösning 8b}} | </div>{{#NAVCONTENT:Svar 8a|3.5 Svar 8|Lösning 8a|3.5 Lösning 8|Lösning 8b|3.5 Lösning 8b}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
== Övning 9 == | == Övning 9 == | ||
| Rad 237: | Rad 237: | ||
Kontrollera om graferna visar de angivna extrema. | Kontrollera om graferna visar de angivna extrema. | ||
</div>{{#NAVCONTENT:Svar 9a|3.5 Svar 9a|Lösning 9a|3.5 Lösning 9a|Lösning 9b|3.5 Lösning 9b}} | </div>{{#NAVCONTENT:Svar 9a|3.5 Svar 9a|Lösning 9a|3.5 Lösning 9a|Lösning 9b|3.5 Lösning 9b}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Versionen från 31 januari 2015 kl. 21.25
| <-- Förra avsnitt | Teori | Övningar |
E-övningar: 1-5
Övning 1
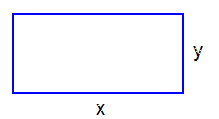
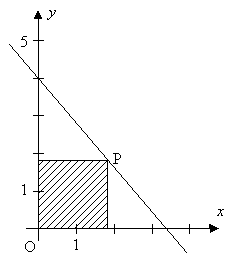
I figuren till höger rör sig punkten \( \, P \, \) på den räta linje vars ekvation är:
Vilken position av \( \, P \, (x, \, y) \, \) ger maximal area till den skuggade rektangeln?
b) Ställ upp problemets målfunktion som en funktion av endast en variabel.
c) Bestäm koordinaterna till punkten \( \, P \, \) så att rektangelns area blir maximal. d) Beräkna rektangelns maximala area. |
|
Hämtar...Övning 2
| En rektangel har omkretsen \( \, 12 \, {\rm cm} \, \). Maximera rektangelns area.
b) Ange problemets målfunktion samt definitionsmängd. c) Bestäm sidorna \( \, x \, \) och \( \, y \, \) så att rektangelns area blir maximal. d) Vad blir rektangelns maximala area? |
|
Övning 3
| En rektangels area är \( \, 25 \, {\rm cm}^2 \, \). Minimera rektangelns omkrets.
b) Ange problemets målfunktion samt definitionsmängd. c) Bestäm sidorna \( \, x \, \) och \( \, y \, \) så att rektangelns omkrets blir minimal. d) Vad blir rektangelns minimala omkrets? |
|
Övning 4
| En rätvinklig triangel är inbunden i en parabel enligt figuren:
Parabeln är definierad genom:
Punkten \( \, P\,(x,\,y) \, \) rör sig på parabeln. Vilken position av \( \, P \, \) ger triangeln största möjliga arean \( \, A \, \)?
b) Ställ upp problemets målfunktion som en funktion \( \, A(x) \, \). c) Bestäm \( \, x \, \) så att \( \, A(x) \, \) antar ett maximum. d) Beräkna triangelns maximala area. |
|
Övning 5
| En fårherde vill samla sina får under en sommarnatt vid en mur i ett inhägnat
rektangulärt område enligt figuren. Han har en stängsel (rep eller dylikt) på \( \, 9 \; {\rm m} \, \) till förfogande. Hur ska han välja rektangulära områdets mått för att få den största möjliga ytan för sina får?
b) Ange målfunktionens definitionsmängd. c) Bestäm \( \, x \, \) så att \( \, A(x) \, \) antar ett maximum. d) Beräkna rektangelns maximala area. e) Rita grafen till målfunktionen \( \, A(x) \, \). f) Skulle en annan geometrisk figur än rektangeln ge större yta för fåren?
|
|
C-övningar: 6-7
Övning 6
| Du ska bygga en öppen låda av en kvadratisk kartong på \( \, 10 \times 10 \; {\rm dm} \, \).
Det gör du genom att skära ut små kvadrater av längden \( \, x \, \) från karton- gens fyra hörn enligt figuren. Hur ska du välja \( \, x \, \) för att få den största möjliga volymen \( \, V \, \) för din öppna låda?
b) Ange målfunktionens definitionsmängd. c) Bestäm \( \, x \, \) så att \( \, V(x) \, \) blir maximal. d) Beräkna lådans maximala volym. e) Rita grafen till målfunktionen \( \, V(x) \, \). f) Vilka mått har lådan med maximal volym? Ange dina svar med två decimaler. |
|
Övning 7
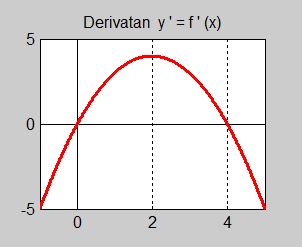
Följande är grafen till derivatan \( {\color{White} x} y' = f'(x) {\color{White} x} \) av en funktion \( \, y = f(x) \, \):
Lös följande uppgifter genom att endast använda grafen ovan:
a) Vilka slutsatser kan man dra om funktionen \( \, y = f(x) \, \) i derivatans nollställen? Motivera dina slutsatser.
b) Sammanfatta dina resultat från a) i en teckentabell och rita en enkel skiss över funktionen \( \, y = f(x)\).
A-övningar: 8-9
Övning 8
Följande funktion är given:
- \[ y = f(x) = {(x - 1)\,(x^2 - 11\,x + 25) \over 3} \]
a) Beräkna koordinaterna till funktionens maximi- resp. minimipunkter exakt.
b) Rita graferna till funktionen \( \, y = f(x) \, \) och derivatan \( \, y\,' = f\,'(x) \, \) i två olika koordinatsystem. Markera funktionens maximi- resp. minimipunkter och derivatans nollställen.
Övning 9
a) Bestäm konstanterna \( \, a, \, b \, \) och \( \, c \, \) så att funktionen
- \[ y = f(x) = a\,x^3 + b\,x^2 + c\,x \]
får ett maximum i punkten \( \, (-1, 7) \, \) och dessutom ett minimum för \( \, x = 2 \, \).
Ange funktionen \( \, y = f(x) \, \).
b) Rita graferna till funktionen \( \, y = f(x) \, \) och dess derivata i två olika koordinatsystem.
Kontrollera om graferna visar de angivna extrema.
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.
