Skillnad mellan versioner av "3.5 Övningar till Extremvärdesproblem"
Taifun (Diskussion | bidrag) m (→Övning 8) |
Taifun (Diskussion | bidrag) m (→Övning 8) |
||
| Rad 243: | Rad 243: | ||
c) Bestäm <math> \, r \, </math> så att <math> \, V(r) \, </math> antar ett maximum. | c) Bestäm <math> \, r \, </math> så att <math> \, V(r) \, </math> antar ett maximum. | ||
| − | d) Beräkna cylinderns maximala | + | d) Beräkna cylinderns maximala volym. |
e) Vilket samband råder mellan cylinderns radie <math> \, r \, </math> och dess höjd <math> \, h \, </math> | e) Vilket samband råder mellan cylinderns radie <math> \, r \, </math> och dess höjd <math> \, h \, </math> | ||
Versionen från 1 februari 2015 kl. 12.03
| <-- Förra avsnitt | Teori | Övningar |
E-övningar: 1-5
Övning 1
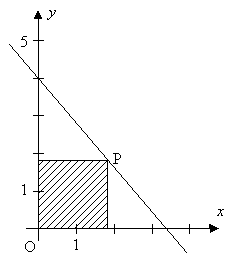
I figuren till höger rör sig punkten \( \, P \, \) på den räta linje vars ekvation är:
Vilken position av \( \, P \, (x, \, y) \, \) ger maximal area till den skuggade rektangeln?
b) Ställ upp problemets målfunktion som en funktion av endast en variabel.
c) Bestäm koordinaterna till punkten \( \, P \, \) så att rektangelns area blir maximal. d) Beräkna rektangelns maximala area. |
|
Hämtar...Övning 2
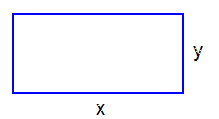
| En rektangel har omkretsen \( \, 12 \, {\rm cm} \, \). Maximera rektangelns area.
b) Ange problemets målfunktion samt definitionsmängd. c) Bestäm sidorna \( \, x \, \) och \( \, y \, \) så att rektangelns area blir maximal. d) Vad blir rektangelns maximala area? |
|
Övning 3
| En rektangels area är \( \, 25 \, {\rm cm}^2 \, \). Minimera rektangelns omkrets.
b) Ange problemets målfunktion samt definitionsmängd. c) Bestäm sidorna \( \, x \, \) och \( \, y \, \) så att rektangelns omkrets blir minimal. d) Vad blir rektangelns minimala omkrets? |
|
Övning 4
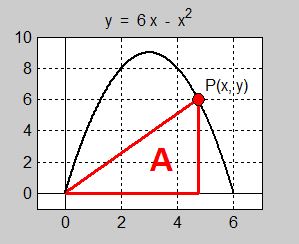
| En rätvinklig triangel är inbunden i en parabel enligt figuren:
Parabeln är definierad genom:
Punkten \( \, P\,(x,\,y) \, \) rör sig på parabeln. Vilken position av \( \, P \, \) ger triangeln största möjliga arean \( \, A \, \)?
b) Ställ upp problemets målfunktion som en funktion \( \, A(x) \, \). c) Bestäm \( \, x \, \) så att \( \, A(x) \, \) antar ett maximum. d) Beräkna triangelns maximala area. |
|
Övning 5
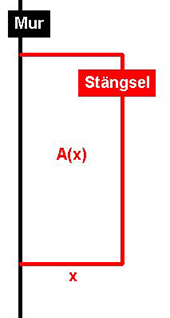
| En fårherde vill samla sina får under en sommarnatt vid en mur i ett inhägnat
rektangulärt område enligt figuren. Han har en stängsel (rep eller dylikt) på \( \, 9 \; {\rm m} \, \) till förfogande. Hur ska han välja rektangulära områdets mått för att få den största möjliga ytan för sina får?
b) Ange målfunktionens definitionsmängd. c) Bestäm \( \, x \, \) så att \( \, A(x) \, \) antar ett maximum. d) Beräkna rektangelns maximala area. e) Rita grafen till målfunktionen \( \, A(x) \, \). f) Skulle en annan geometrisk figur än rektangeln ge större yta för fåren?
|
|
C-övningar: 6-7
Övning 6
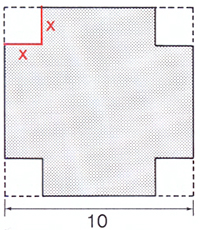
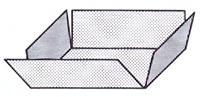
| Du ska bygga en öppen låda av en kvadratisk kartong på \( \, 10 \times 10 \; {\rm dm} \, \).
Det gör du genom att skära ut små kvadrater av längden \( \, x \, \) från karton- gens fyra hörn enligt figuren. Hur ska du välja \( \, x \, \) för att få den största möjliga volymen \( \, V \, \) för din öppna låda?
b) Ange målfunktionens definitionsmängd. c) Bestäm \( \, x \, \) så att \( \, V(x) \, \) blir maximal. d) Beräkna lådans maximala volym. e) Rita grafen till målfunktionen \( \, V(x) \, \). f) Vilka mått har lådan med maximal volym? Ange dina svar med två decimaler. |
|
Övning 7
SJ har \( \, 20\,000 \, \) passagerare per månad på en viss bansträcka med ett biljettpris på \( \, 200 \, \) kr.
En marknadsundersökning visar att varje höjning av biljettpriset med \( \, 1 \, \) kr skulle medföra en förlust av \( \, 80 \, \) passagerare per månad.
Vilken biljettprishöjning kommer att maximera intäkten per månad?
a) Ange problemets bivillkor om:
- \[ x \, = \, {\rm Den\;planerade\;prishöjningen\;i\;kr.} \]
- \[ y \, = \, {\rm Antalet\;passagerare\;per\;månad\;efter\;en\;sådan\;prishöjning.} \]
b) Ställ upp problemets målfunktionen \( \, I(x) \, \) för SJ:s intäkt per månad.
c) Bestäm \( \, x \, \) så att intäkten \( \, I(x) \, \) blir så stor som möjligt.
d) Beräkna den maximala intäkten efter en biljettprishöjning på \( \, x \, \) kr.
e) För vilka prishöjningar kommer det inte längre att löna sig att höja biljettpriset?
A-övningar: 8-9
Övning 8
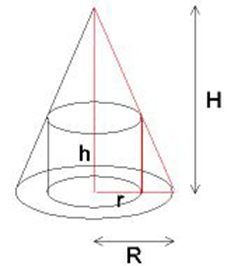
En cylinder är placerad inuti en kon enligt figuren. Kons mått är givna:
Vilken radie \( \, r \, \) och höjd \( \, h \, \) ger cylindern största möjliga volymen \( \, V \, \)?
b) Ställ upp problemets målfunktion som en funktion \( \, V(r) \, \). c) Bestäm \( \, r \, \) så att \( \, V(r) \, \) antar ett maximum. d) Beräkna cylinderns maximala volym. e) Vilket samband råder mellan cylinderns radie \( \, r \, \) och dess höjd \( \, h \, \)
|
|
Övning 9
| För att producera en cylinderformad konservburk har man en viss mängd \( \, A \, \)
plåt till förfogande (efter spill). Dvs cylinderns begränsningsarea \( \, = \, A \; {\rm cm}^2 \, \). Vilka mått på konserven maximerar volymen?
b) Ställ upp problemets målfunktion. c) Bestäm cylinderns radie och höjd så att burkens volym blir maximal. d) Visa att för en cylinder med maximal volym, radien \( \, r \, \) och höjden \( \, h \, \) gäller:
|
Fil:Konservburk 40.jpg
|
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.
