Skillnad mellan versioner av "2.7 Numerisk derivering"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 41: | Rad 41: | ||
=== <b><span style="color:#931136">Framåtdifferenskvoten = derivatans definition utan limes</span></b> === | === <b><span style="color:#931136">Framåtdifferenskvoten = derivatans definition utan limes</span></b> === | ||
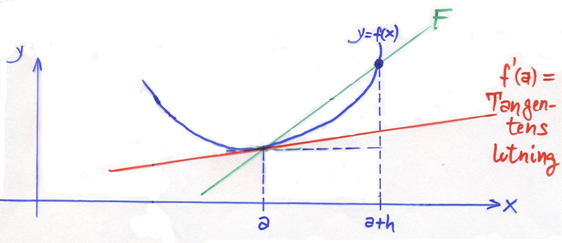
| − | Derivatan <math> f\,'(a) </math> av funktionen <math> y = f\,(x) </math> i punkten <math> x = a\, </math> kan approximeras med <strong><span style="color:#931136">Framåtdifferenskvoten</span></strong>: | + | Derivatan <math> f\,'(a) </math> av funktionen <math> y = f\,(x) </math> i punkten <math> x = a\, </math> kan approximeras (man kan närma sig derivatan) med <strong><span style="color:#931136">Framåtdifferenskvoten</span></strong>: |
<table> | <table> | ||
<tr> | <tr> | ||
| Rad 53: | Rad 53: | ||
<math> h\, </math> kallas <strong><span style="color:red">steglängden</span></strong> och kan väljas fritt. Små värden för <math> h\, </math> rekommenderas. | <math> h\, </math> kallas <strong><span style="color:red">steglängden</span></strong> och kan väljas fritt. Små värden för <math> h\, </math> rekommenderas. | ||
| − | Approximationen blir desto bättre ju mindre steglängden är. | + | Approximationen (närmevärdet) blir desto bättre ju mindre steglängden är. |
</td> | </td> | ||
<td> [[Image: FramåtDiff.jpg]]</td> | <td> [[Image: FramåtDiff.jpg]]</td> | ||
Versionen från 1 december 2015 kl. 13.31
| <-- Förra avsnitt | Genomgång | Övningar | Diagnosprov kap 2 Derivatan | Lösningar till diagnosprov kap 2 |
Lektion 22 Numerisk derivering
Varför numerisk derivering?
Varför ska vi lära oss numerisk derivering när vi kan derivera med hjälp av derivatans definition och de deriveringsregler vi ställde upp i de två sista avsnitten?
Exempel
Följande funktioner matchar inte mot någon av funktionstyperna från Uppdaterad ta-
bell över eriveringsregler och kan därför inte deriveras med våra deriveringsregler:
- \[ y \, = \, \displaystyle {1 \over x + 1} \qquad\qquad y \, = \, {1 \over e^x + 1} \qquad\qquad y \, = \, \ln x \qquad \]
Bl.a. därför är det motiverat att syssla med alternativa lösningar. Numerisk derivering är en av dem. Läs mer: När ska man använda numerisk derivering?.
Numerisk derivering är en metod för ungefärlig beräkning av derivatan utan att behöva använda limes i derivatans definition. Med hjälp av numeriska deriveringsformler som man ställer upp, kan ett närmevärde för derivatan beräknas.
Man går tillbaka till deriveringens rötter, nämligen till genomsnittlig förändringshastighet som även betecknas med differenskvot. Alla numeriska deriveringsformler baseras på differenskvoten, fast på olika sätt. Vi kommer att behandla här de tre enklaste numeriska deriveringsformlerna:
- Framåtdifferenskvoten
- Bakåtdifferenskvoten
- Centrala differenskvoten
Framåtdifferenskvoten = derivatans definition utan limes
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras (man kan närma sig derivatan) med Framåtdifferenskvoten:
Exempel
Följande funktion \( \, f(x) \, \) är given i tabellform. Beräkna \( \, f\,'(0,6) \, \) med framåtdifferenskvoten.
\( x\, \) \( f(x)\, \) \( 0,5\, \) \( 1,79744\, \) \( 0,6\, \) \( 2,04424\, \) \( 0,7\, \) \( 2,32751\, \)
Lösning:
Steglängden \( h = 0,1\, \) är given i tabellen.
\[ f\,'(0,6) = {f(0,6 + 0,1) - f(0,6) \over 0,1} = {f(0,7) - f(0,6) \over 0,1} = {2,32751 - 2,04424 \over 0,1} = {0,28327 \over 0,1} = 2,8327 \]
Bakåtdifferenskvoten
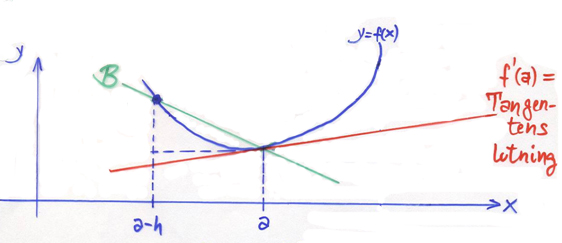
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Bakåtdifferenskvoten:
Exempel
Funktionen \( \, f(x) = \ln x \, \) är given. Välj steglängden \( \, h = 0,01 \, \) och beräkna \( \, f\,'(1,8) \, \) med bakåtdifferenskvoten.
Lösning:
\[ f\,'(1,8) \approx {f(1,8) - f(1,8 - 0,01) \over 0,01} = {f(1,8) - f(1,79) \over 0,01} = {\ln(1,8) - \ln(1,79) \over 0,01} = 0,5571 \]
Om det exakta värdet (avrundat till 4 decimaler) är \( \, f\,'(1,8) = 0,5556 \, \) kan närmevärdets fel definieras som:
Vårt närmevärdes fel blir då:
- Felet \( \, = \, |\,0,5556 \, - \, 0,5571| \, = \, 0,0015\)
Närmevärdefelets definition ger oss en möjlighet att jämföra de olika numeriska deriveringsformlernas noggrannhet, se övning 3.
Centrala differenskvoten
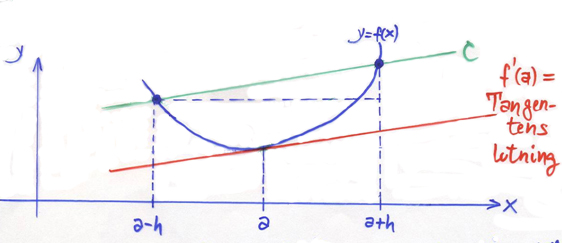
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Centrala differenskvoten
\( \quad f\,'(a) \qquad\;\, \approx \displaystyle \qquad {f(a + h) \, - \, f(a-h) \over 2\,h} \quad \)
För 2:a gradsfunktioner är formeln exakt för alla \( \,h \), se satsen nedan. |
 |
Exempel
Funktionen \( \, f(x) = x\,^2 \, \) är given. Välj steglängden \( \, h = 0,5 \, \) och beräkna \( \, f\,'(1) \, \) med centrala differenskvoten.
Lösning:
\[ f\,'(1) \approx {f(1 + 0,5) - f(1 - 0,5) \over 2\cdot 0,5} = {f(1,5) - f(0,5) \over 2\cdot 0,5} = {1,5^2 - 0,5^2 \over 1} = {\color{Red} 2} \]
Funktionens derivata är \( \, f\,'(x) = 2\,x \, \) och därmed är det exakta värdet \( f\,'(1) = 2 \cdot 1 = {\color{Red} 2} \).
Noggrannhetsfrågor
Är det en slump att den numeriska deriveringen med centrala differenskvoten i exemplet ovan ger exakt värde, fast steglängden är relativt stor?
Svaret är nej: Den centrala differenskvoten deriverar alla 2:a gradsfunktioner (och förstås även alla 1:a gradsfunktioner) exakt oberoende av steglängden. Här följer satsen samt beviset:
Sats:
Den centrala differenskvoten ger den exakta derivatan till
alla 2:a gradsfunktioner oberoende av steglängden.
- Om \( f(x) \; = \; x^2 + b\,x + c \) då:
- \[ {f(x + h) \, - \, f(x-h) \over 2\,h} \; = \; 2\,x + b \; = \; f\,'(x) \]
Bevis:
\[ f(x + h) = (x+h)^2 + b\,(x+h) + c = x^2 + 2\,x\,h + h^2 + b\,x + b\,h + c \]
\[ f(x - h) = (x-h)^2 + b\,(x-h) + c = x^2 - 2\,x\,h + h^2 + b\,x - b\,h + c \]
\[ f(x + h) - f(x-h) = x^2 + 2\,x\,h + h^2 + b\,x + b\,h + c - (x^2 - 2\,x\,h + h^2 + b\,x - b\,h + c) = 4\,x\,h + 2\,b\,h = 2\,h\,(2\,x + b) \]
\[ {f(x + h) - f(x-h) \over 2\,h} = {{\color{Red} {2\,h}}\,(2\,x + b) \over {\color{Red} {2\,h}}} = 2\,x + b = f\,'(x) \]
Att resultatet är oberoende av steglängden visas i beviset ovan genom att \( h\, \) förkortas bort och inte längre förekommer i slutresultatet.
Utan att bevisa ska också nämnas att framåt-och bakåtdifferenskvoten ger den exakta derivatan till alla 1:a gradsfunktioner oberoende av steglängden.
När ska man använda numerisk derivering?
Det finns typer av funktioner som inte matchar någon av de deriveringsregler vi lärt oss hittills. Det finns t.o.m. typer av funktioner som inte har någon analytisk derivata alls. Dvs deras derivata kan inte anges i form av ett algebraiskt uttryck. I andra sammanhang kan det det i praktiken vara svårt \(-\) ibland kanske onödigt \(-\) att beräkna derivatan exakt.
I följande situationer är det nödvändigt resp. rimligt att använda numerisk derivering:
1) Vi kan inte hitta en matchande formel bland våra deriveringsregler. T.ex. följande funktion ska deriveras:
- \[ f(x) = {1 \over x + 1} \]
- Vi konstaterar att den inte matchar mot någon funktionstyp i vår deriveringstabell. \( \, f(x) \) kan inte skrivas om till en potens med basen \( \, x \), vilket vi t.ex. kunde göra med \( y = \displaystyle {1 \over x} \) genom att skriva om den till \( y = \, x^{-1} \). Sedan kunde vi använda deriveringsregeln för derivatan av en potens på denna omskrivna formen \( y = \, x^{-1} \). Eftersom en sådan omskrivning inte går att göra med funktionen \( f(x) = \displaystyle {1 \over x + 1}\, \) kan den inte deriveras med denna regel. Inte heller med någon annan av de deriveringsregler vi känner till hittills. Det är nämnaren \(\, x + 1 \) som gör att uttrycket inte kan skrivas om till en potens med basen \( \, x \). Visserligen går det att skriva om så här: \( \, f(x) = \displaystyle {1 \over x + 1} = (x + 1)^{-1} \), men basen här är inte \( \, x \) utan \( \, x + 1 \).
- Funktionen i fråga kan anses som en kvot av två funktioner, nämligen \( \, g(x) = 1 \) och \( \, h(x) = x + 1 \). En deriveringsregel för en kvot av funktioner, den s.k. kvotregeln som skulle kunna användas här, kommer vi att lära oss först i Matte 4-kursen.
- Ett annat exempel är funktionen:
- \[ f(x) = \displaystyle {1 \over e^x + 1}\, \]
- som inte heller matchar mot någon funktionstyp i vår deriveringstabell \(-\) av liknande anledning som exemplet ovan. Även den går att derivera med hjälp av kvotregeln.
- Ytterligare exempel på en funktion som inte matchar mot någon funktionstyp i vår deriveringstabell, är:
- \[ f(x) = \ln x\, \]
- I exemplet på bakåtdifferenskvoten visades hur man kunde derivera \( \ln x \) numeriskt.
2) Funktionen som ska deriveras är given endast i tabellform.
- Som exempel tar vi den funktion i tabellform som vi behandlade i aktiviteten Introduktion till derivatan och som beskriver kroppens rörelse vid hopp från 10 meters torn. Låt oss här anta att vi inte tagit fram den från någon formel. \( x\, \) är tiden och \( f(x)\, \) höjden över vattnet:

- Sådana funktioner i tabellform förekommer ofta i statistiken och i tillämpningarna som resultat av mätningar. De visar ett samband utan någon formel. Ändå uppfyller de definitionen på en funktion, nämligen att vara en
- "Regel som tilldelar varje \( x\, \)-värde endast ett \( y\, \)-värde."
- Även en sådan funktion har en derivata, både i varje punkt (av sitt definitionsområde) och som en ny funktion. Men i båda fall kan derivatan tas fram endast numeriskt. Vi hade gjort detta i aktiviteten Introduktion till derivatan. Den nya funktionen som representerar derivatan hade vi approximerat numeriskt genom att använda framåtdifferenskvoten, där formulerad som \( \displaystyle {\Delta y \over \Delta x} \). Resultatet visades i Lösningen till aktiviteten både i tabellform (punkt 4) och grafiskt (punkt 6). Även om resultatet var approximativt visade grafen tydligt att den ursprungliga kvadratiska funktionens derivata var en linjär funktion.
3) Funktionens derivata blir så komplicerad att det tar mer tid att ställa upp den (och risken för felräkning ökar) än att derivera den numeriskt.
- Exempel:
- \[ f(x) = {\sin\,3\,x \over 4\,\cos\,x} \qquad\qquad\qquad\qquad f\,'(x) = {12\,\cos\,3\,x \cdot \cos\,x \,+\, 4\,\sin\,3\,x \cdot \sin\,x \over 16\,\cos^2\,x} \]
- För det första är det inte enkelt att ställa upp \( f\,'(x) \). Även här skulle kvotregeln behövas samt deriveringsreglerna för sinus- och cosinusfunktioner.
- För det andra ser man att det är väsentligt enklare att beräkna t.ex. \( f(2)\, \) än \( f\,'(2) \). I de numeriska deriveringsformlerna ingår nämligen endast beräkningar av \( f(x)\, \), inte av \( f\,'(x) \).
Copyright © 2011-2015 Taifun Alishenas. All Rights Reserved.