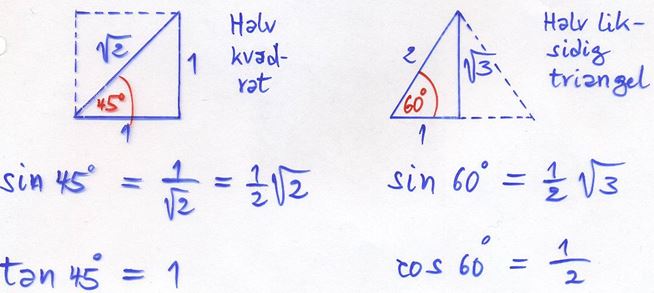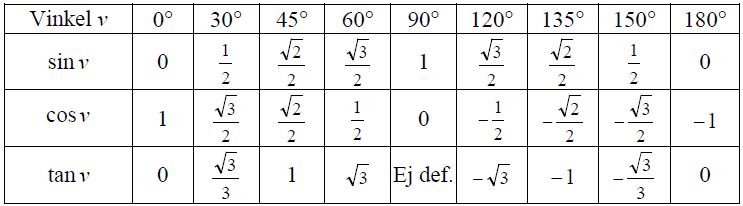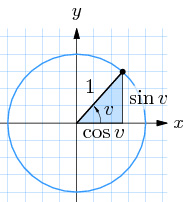Skillnad mellan versioner av "Kapitel 5 Trigonometri"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 4: | Rad 4: | ||
{{Not selected tab|[[Huvudsida|Start Matte 3c]]}} | {{Not selected tab|[[Huvudsida|Start Matte 3c]]}} | ||
{{Not selected tab|[[Matte 3c Planering|Planering Matte 3c]]}} | {{Not selected tab|[[Matte 3c Planering|Planering Matte 3c]]}} | ||
| − | {{ | + | {{Selected tab|[[Media: Formelsamling NP Ma3 Trig.pdf|Formelsamling Trigonometri]]}} |
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
Versionen från 18 mars 2016 kl. 14.08
| Start Matte 3c | Planering Matte 3c | Formelsamling Trigonometri |
Utdrag ur planeringen:
5.1 Trigonometri i rätvinkliga trianglar
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 208
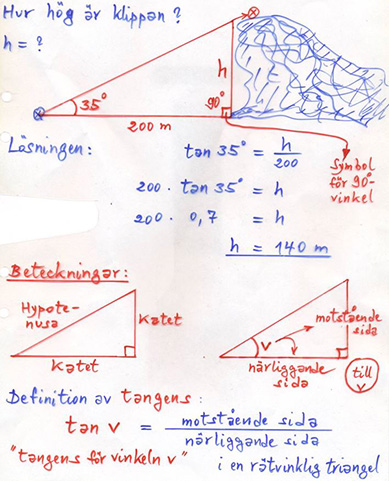
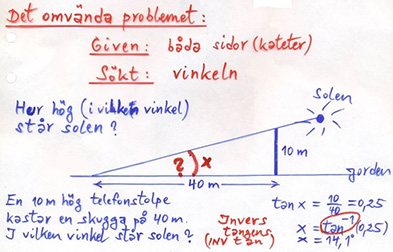
Tangens för \( \, v \, < \, 90^\circ \)
|
|
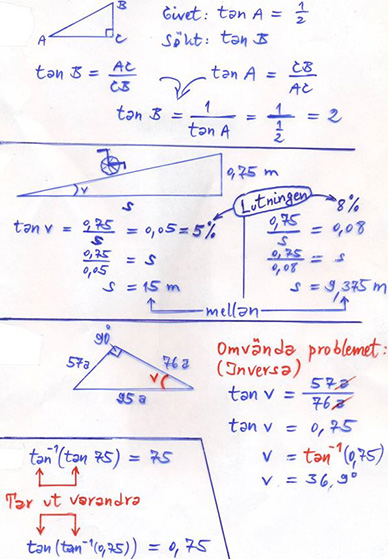
Exempel på tangens
Sinus och Cosinus för \( \, v \, < \, 90^\circ \)
5.2 Exakta trigonometriska värden / Enhetscirkeln
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 209 / 210
Två speciella vinklar: \( \, 45^\circ \, \) och \( \, 60^\circ \, \)
Använd Pythagoras satsen på halva kvadraten (\( 45^\circ \)) och på halva liksidiga triangeln (\( 60^\circ \)):
"Exakt" betyder: Gå inte över till decimaltal, dvs bibehåll bråken (med heltal i täljaren och nämnaren) samt rötter som inte ger heltal.
Ytterligare exakta trigonometriska värden
Andra elementära geometriska satser ger följande exakta värden:
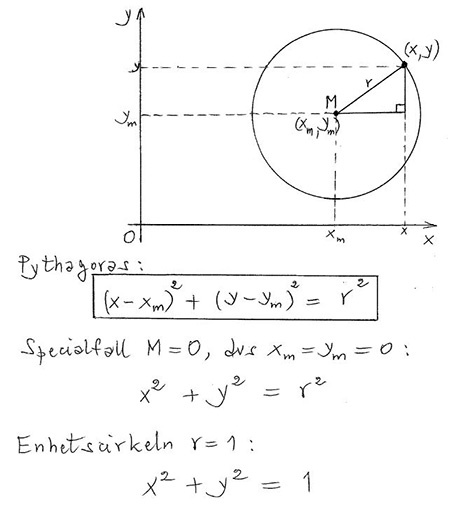
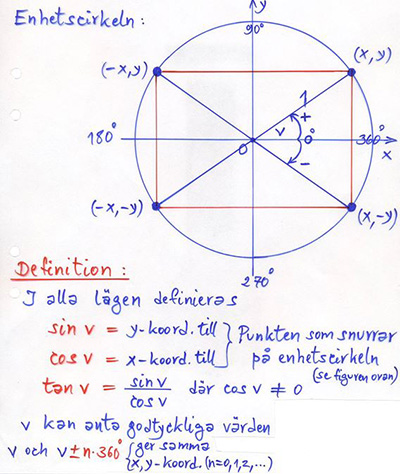
Enhetscirkeln
Cirkel \( \, = \, \) Mängden av alla punkter som har samma avstånd (radien \( \, r \, \)) från en punkt (medelpunkten \( \, M \, \)).
Cirkelns ekvation:
Enhetscirkeln är cirkeln med radien \( \, r \, = \, 1 \, \) och medelpunkten \( \, M \, = \, 0 \, \) (origo):
Om en punkt \( \, P\,(x, y) \, \) snurrar på enhetscirkeln, så gäller:
\(\begin{array}{rcl} x & = & \cos v \\ y & = & \sin v \end{array}\)
I cirklar med radien \( \, r \, > \, 1 \, \) förblir vinkeln \( \, v \, \) den samma och därmed \( \, \cos v = \displaystyle \frac{r \cdot \; x}{r} = x \, \) och \( \, \sin v = \displaystyle \frac{r \cdot \; y}{r} = y \), precis som ovan.
Detta används för att definiera de trigonometriska funktionerna i godtyckliga trianglar, dvs för vinklar \( \, v \, \geq \, 90^\circ \, \).
5.3 Godtyckliga trianglar
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 215
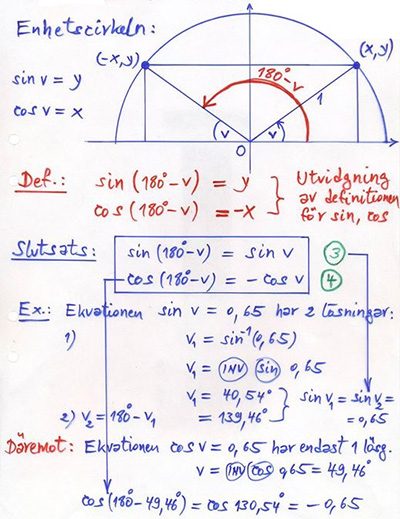
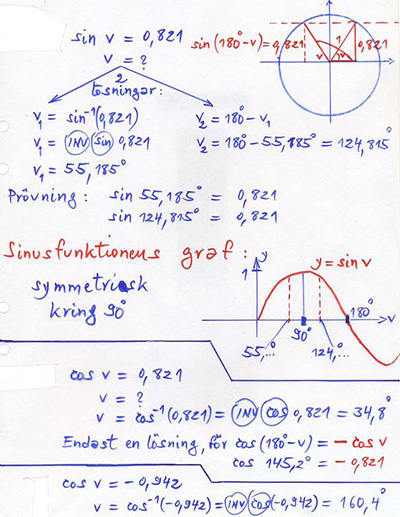
Sinus och Cosinus för vinklar: \( \quad 90^\circ \, \leq \, v \, \leq \, 180^\circ \)
| Exempel:
|
Sinus, Cosinus och Tangens för alla vinklar
5.4 Triangelsatserna: Areasatsen
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 218
Areasatsen
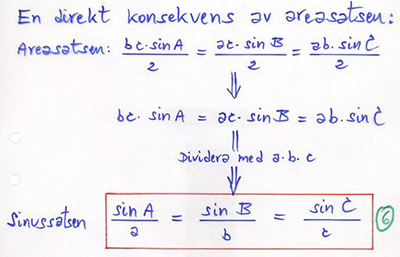
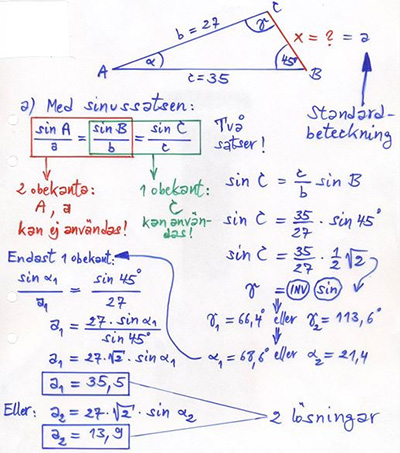
5.5 Sinussatsen / Sinussatsens två fall
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 220 / 224-225
Sinussatsen
Sinussatsens två fall
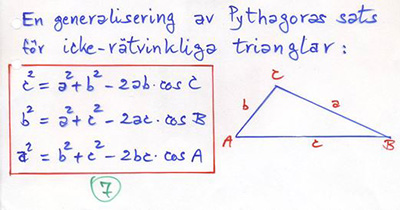
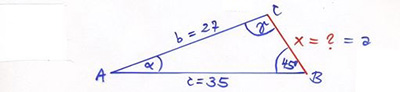
5.6 Cosinussatsen
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 229-230
Cosinussatsen
Exempel på Cosinussatsen
5.7 Användning av trigonometri
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 232-233
Copyright © 2011-2016 Math Online Sweden AB. All Rights Reserved.