Skillnad mellan versioner av "2.4 Derivatans definition"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 9: | Rad 9: | ||
| − | [[Media: Lektion 19 Derivatans def I Rutaa.pdf|< | + | [[Media: Lektion 19 Derivatans def I Rutaa.pdf|<b><span style="color:blue">Lektion 19 Derivatans definition I</span></b>]] |
| − | [[Media: Lektion 20 Derivatans def II Ruta.pdf|< | + | [[Media: Lektion 20 Derivatans def II Ruta.pdf|<b><span style="color:blue">Lektion 20 Derivatans definition II</span></b>]] |
__NOTOC__ | __NOTOC__ | ||
<big> | <big> | ||
| Rad 22: | Rad 22: | ||
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td>En oljetank läcker genom ett hål i tankens botten ([[2.2_Genomsnittlig_förändringshastighet#Exempel_3_Oljetank|< | + | <td>En oljetank läcker genom ett hål i tankens botten ([[2.2_Genomsnittlig_förändringshastighet#Exempel_3_Oljetank|<b><span style="color:blue">Exempel 3</span></b>]] i förra avsnitt). |
Oljans utströmning beskrivs av funktionen: | Oljans utströmning beskrivs av funktionen: | ||
| Rad 31: | Rad 31: | ||
:::<math> y \, = \, {\rm Oljans\;volym\;i\;liter} </math> | :::<math> y \, = \, {\rm Oljans\;volym\;i\;liter} </math> | ||
| − | <b>a)</b> Beräkna oljans < | + | <b>a)</b> Beräkna oljans <b><span style="color:red">genomsnittliga</span></b> utströmningshastighet i intervallet <math> \, 0 \,\leq\, x \,\leq\, h \quad </math> |
<math> \;\;\, </math> som ett uttryck i <math> \, h > 0 \, </math> (något positivt tal). | <math> \;\;\, </math> som ett uttryck i <math> \, h > 0 \, </math> (något positivt tal). | ||
| − | <b>b)</b> Beräkna oljans < | + | <b>b)</b> Beräkna oljans <b><span style="color:red">momentana</span></b> utströmningshastighet i punkten <math> \, x = 0 </math> genom att |
<math> \;\;\, </math> i uttrycket från <b>a)</b> låta <math> \, h \, </math> gå mot <math> \, 0 </math>. | <math> \;\;\, </math> i uttrycket från <b>a)</b> låta <math> \, h \, </math> gå mot <math> \, 0 </math>. | ||
| Rad 49: | Rad 49: | ||
<div class="exempel"> | <div class="exempel"> | ||
| − | <b>a)</b> Den allmänna definitionen av [[2.2_Genomsnittlig_förändringshastighet#Allm.C3.A4n_definition|< | + | <b>a)</b> Den allmänna definitionen av [[2.2_Genomsnittlig_förändringshastighet#Allm.C3.A4n_definition|<b><span style="color:blue">genomsnittlig förändringshastighet</span></b>]] är: |
::<math> {\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h} \qquad {\rm i\;\;intervallet } \qquad x_1 \,\leq\, x \,\leq\, x_1 + h </math> | ::<math> {\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h} \qquad {\rm i\;\;intervallet } \qquad x_1 \,\leq\, x \,\leq\, x_1 + h </math> | ||
| Rad 59: | Rad 59: | ||
För <math> \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, </math> får vi <math> \, f\,(h) \, = \, 4\,h^2 - 380\,h + 9\,000 \, </math> och <math> \, f\,(0) \, = \, 9\,000 </math>. | För <math> \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, </math> får vi <math> \, f\,(h) \, = \, 4\,h^2 - 380\,h + 9\,000 \, </math> och <math> \, f\,(0) \, = \, 9\,000 </math>. | ||
| − | Då blir oljans < | + | Då blir oljans <b><span style="color:red">genomsnittliga</span></b> utströmningshastighet i intervallet <math> 0 \,\leq\, x \,\leq\, h \, </math>: |
::<math> {\Delta y \over \Delta x} \,=\, {f(h) \, - \, f(0) \over h} \,=\, {4\,h^2 - 380\,h + 9\,000 \,-\, 9\,000 \over h} \,=\, {4\,h^2 - 380\,h \over h} \,=\, {{\color{Red} h}\,(4\,h - 380) \over {\color{Red} h}} \,=\, 4\,h - 380 </math> | ::<math> {\Delta y \over \Delta x} \,=\, {f(h) \, - \, f(0) \over h} \,=\, {4\,h^2 - 380\,h + 9\,000 \,-\, 9\,000 \over h} \,=\, {4\,h^2 - 380\,h \over h} \,=\, {{\color{Red} h}\,(4\,h - 380) \over {\color{Red} h}} \,=\, 4\,h - 380 </math> | ||
| − | <b>b)</b> Nu låter vi i uttrycket <math> 4\,h - 380 </math> för den genomsnittliga utströmningshastigheten <math> \, h\, </math> gå mot <math> 0\, </math> för att få oljans < | + | <b>b)</b> Nu låter vi i uttrycket <math> 4\,h - 380 </math> för den genomsnittliga utströmningshastigheten <math> \, h\, </math> gå mot <math> 0\, </math> för att få oljans <b><span style="color:red">momentana</span></b> utströmningshastighet i <math> \, x = 0\, </math>. |
Dvs vi beräknar gränsvärdet<span style="color:black">:</span> | Dvs vi beräknar gränsvärdet<span style="color:black">:</span> | ||
| Rad 69: | Rad 69: | ||
:::::::::<math> \qquad \displaystyle \lim_{h \to 0}\, {(4\,h - 380)} \,=\, -\,380 </math> | :::::::::<math> \qquad \displaystyle \lim_{h \to 0}\, {(4\,h - 380)} \,=\, -\,380 </math> | ||
| − | <math> -\,380\, </math> är oljans < | + | <math> -\,380\, </math> är oljans <b><span style="color:red">momentana</span></b> utströmningshastighet i <math> \, x = 0 \, </math>. Dvs vid denna tidpunkt sjunker oljan med exakt <math> 380\, </math> liter per minut. |
| − | Ett annat ord för den momentana utströmningshastigheten är < | + | Ett annat ord för den momentana utströmningshastigheten är <b><span style="color:red">derivatan</span></b>: |
<div class="border-div"> | <div class="border-div"> | ||
| − | Funktionen <math> \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, </math> har i punkten <math> \, x = 0 \; </math> < | + | Funktionen <math> \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, </math> har i punkten <math> \, x = 0 \; </math> <b><span style="color:red">derivatan</span></b> <math> \; -\,380 \; </math>. |
| − | Man skriver<span style="color:black">:</span> <math> \; f\,{\color{Red} '}(0) \,=\, -\,380 \; </math> och läser: "<math> \, f </math> < | + | Man skriver<span style="color:black">:</span> <math> \; f\,{\color{Red} '}(0) \,=\, -\,380 \; </math> och läser: "<math> \, f </math> <b><span style="color:red">prim</span></b> av <math> \, 0 \, </math> är <math> \; -\,380 \; </math>" . |
</div> | </div> | ||
</div> | </div> | ||
| Rad 97: | Rad 97: | ||
Exemplet ovan visar att derivatan av en andragradsfunktion (parabel) är en linjär funktion (rät linje). | Exemplet ovan visar att derivatan av en andragradsfunktion (parabel) är en linjär funktion (rät linje). | ||
| − | Medan vi i [[2.4_Derivatans_definition#Exempel_Oljetank|< | + | Medan vi i [[2.4_Derivatans_definition#Exempel_Oljetank|<b><span style="color:blue">Exemplet Oljetank</span></b>]] beräknade derivatan i en punkt som ett tal, anger exemplet ovan derivatan som en ny funktion. Hur kommer denna nya syn på derivatan till? |
| − | Den nya derivatfunktionen får man genom att betrakta punkten <math> \, a \, </math> inte längre som en konstant utan som en variabel <math> \, x </math>. Med andra ord, man tillämpar definitionen av derivatan i en punkt på varenda punkt <math> \, a \, </math> på <math> \, x</math>-axeln. Tänker man sig att alla dessa derivatvärden är tilldelade sina respektive <math> \, x</math>-värden, bildar denna tilldelning en < | + | Den nya derivatfunktionen får man genom att betrakta punkten <math> \, a \, </math> inte längre som en konstant utan som en variabel <math> \, x </math>. Med andra ord, man tillämpar definitionen av derivatan i en punkt på varenda punkt <math> \, a \, </math> på <math> \, x</math>-axeln. Tänker man sig att alla dessa derivatvärden är tilldelade sina respektive <math> \, x</math>-värden, bildar denna tilldelning en <b><span style="color:red">ny funktion</span></b> som är den ursprungliga <b><span style="color:red">funktionens derivata</span></b>, fast inte längre som ett tal utan som ett uttryck i <math> \, x </math>. |
| Rad 106: | Rad 106: | ||
<div class="border-divblue"> | <div class="border-divblue"> | ||
| − | < | + | <b><span style="color:red">Derivatan</span></b> av funktionen <math> \, y = f\,(x) \, </math> är <math> \, \displaystyle f\,\,{\color{Red} '}\,\,(x) \; = \; \lim_{h \to 0}\,\,{f(x + h) \, - \, f(x) \over h} </math> |
| − | <math> {\color{Red} '} \; </math> är symbolen för derivatan. <math> \;\, f\,{\color{Red} '}(x) \; </math> läses så här: "<math> \, f </math> < | + | <math> {\color{Red} '} \; </math> är symbolen för derivatan. <math> \;\, f\,{\color{Red} '}(x) \; </math> läses så här: "<math> \, f </math> <b><span style="color:red">prim</span></b> av <math> \, x \, </math>" . |
</div> | </div> | ||
| Rad 122: | Rad 122: | ||
:::<math> y \, = \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 </math> | :::<math> y \, = \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 </math> | ||
| − | <b>a)</b> Ställ upp funktionens [[2.2_Genomsnittlig_förändringshastighet#Allm.C3.A4n_definition|< | + | <b>a)</b> Ställ upp funktionens [[2.2_Genomsnittlig_förändringshastighet#Allm.C3.A4n_definition|<b><span style="color:blue">genomsnittliga förändringshastighet</span></b>]] <math> \, \displaystyle{\Delta y \over \Delta x} \, </math> som ett uttryck i <math> \, x \, </math> och <math> \, h </math>. |
<b>b)</b> Ange derivatan av <math> \, f\,(x) \, </math> som en ny funktion av <math> \, x \, </math> genom att i <math> \, \displaystyle{\Delta y \over \Delta x} \, </math> låta <math> \, h \, </math> gå mot <math> \, 0 </math>. | <b>b)</b> Ange derivatan av <math> \, f\,(x) \, </math> som en ny funktion av <math> \, x \, </math> genom att i <math> \, \displaystyle{\Delta y \over \Delta x} \, </math> låta <math> \, h \, </math> gå mot <math> \, 0 </math>. | ||
| Rad 153: | Rad 153: | ||
<div class="border-div"> | <div class="border-div"> | ||
| − | Funktionen <math> \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, </math> har < | + | Funktionen <math> \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, </math> har <b><span style="color:red">derivatan</span></b> <math> \; f\,'\,(x) = 8\,x - 380 \; </math>. |
</div> | </div> | ||
| Rad 165: | Rad 165: | ||
| − | I efterhand kan vi nu verifiera det i [[2.4_Derivatans_definition#Exempel_Oljetank|< | + | I efterhand kan vi nu verifiera det i [[2.4_Derivatans_definition#Exempel_Oljetank|<b><span style="color:blue">Exempel Oljetank</span></b>]] beräknade värdet av <math> f\,(x)</math>:s derivata i punkten <math> \, x = 0 </math> genom att sätta in <math> \, x = 0 </math> i derivatans funktion <math> f\,'\,(x) = 8\,x - 380 </math>: |
::::::::::<math> f\,'\,(0) \,=\, 8 \cdot 0 - 380 \,=\, 0 - 380 \,=\, -\,380 </math> | ::::::::::<math> f\,'\,(0) \,=\, 8 \cdot 0 - 380 \,=\, 0 - 380 \,=\, -\,380 </math> | ||
| Rad 171: | Rad 171: | ||
Vid tiden <math> \, x = 0 \, </math> sjönk oljan med <math> \, 380\, </math> liter per minut som var den största utströmningshastigheten när oljan hade mest volym och utövade det största trycket på hålet. | Vid tiden <math> \, x = 0 \, </math> sjönk oljan med <math> \, 380\, </math> liter per minut som var den största utströmningshastigheten när oljan hade mest volym och utövade det största trycket på hålet. | ||
| − | Tidigare [[2.2_Genomsnittlig_förändringshastighet#Exempel_3_Oljetank|< | + | Tidigare [[2.2_Genomsnittlig_förändringshastighet#Exempel_3_Oljetank|<b><span style="color:blue">(Exempel 3 d)</span></b>]] hade vi fått <math> -\,379,6\, </math> för den genomsnittliga utströmningshastighet i intervallet <math> 0 \,\leq\, x \,\leq\, 0,1 </math>, vilket är ett närmevärde för derivatan, som nu visar sig vara ganska bra. Närmevärdet hade blivit ännu precisare om vi hade valt t.ex. intervallet <math> 0 \,\leq\, x \,\leq\, 0,01 </math> eller <math> 0 \,\leq\, x \,\leq\, 0,001 </math> osv. Det exakta värdet <math> -\,380 \, </math> får man om man i intervallet <math> 0 \,\leq\, x \,\leq\, h </math> låter <math> h \to 0 </math>. |
Dessutom får vi genom grafen ovan för tredje gången en bekräftelse på följande sats som kommer att bevisas generellt senare: | Dessutom får vi genom grafen ovan för tredje gången en bekräftelse på följande sats som kommer att bevisas generellt senare: | ||
| Rad 179: | Rad 179: | ||
| − | Det första exemplet på denna sats hade vi sett i kapitlets inledande [[2.1_Lösning_till_Aktiviteten_Introduktion_till_derivata|< | + | Det första exemplet på denna sats hade vi sett i kapitlets inledande [[2.1_Lösning_till_Aktiviteten_Introduktion_till_derivata|<b><span style="color:blue">Aktivitet</span></b> (Lösning, punkt 6)]] då vi ritade grafen till hastighetsfunktionen till Yulias hopp från 10 m-torn. Det andra var när vi i detta avsnitt i [[2.4_Derivatans_definition#Derivatan_som_en_funktion|<b><span style="color:#931136">Derivatan som en funktion</span></b>]] såg grafen till derivatan <math> \, y\,' = \, 10\,x \, </math> av funktionen <math> \, y \, = \, 5\,x^2 \, </math>. |
| − | I hela exemplet Oljetank är oljans momentana utströmningshastighet derivatans < | + | I hela exemplet Oljetank är oljans momentana utströmningshastighet derivatans <b><span style="color:red">fysikaliska tolkning</span></b>. |
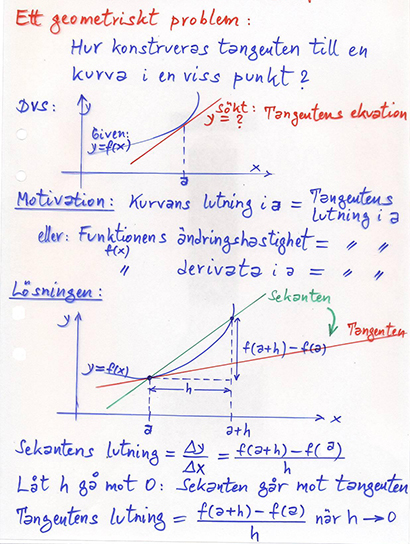
| − | Men derivatan har även en < | + | Men derivatan har även en <b><span style="color:red">geometrisk tolkning</span></b> som är ganska intuitiv: |
=== <b><span style="color:#931136">Från sekanten till tangenten</span></b> === | === <b><span style="color:#931136">Från sekanten till tangenten</span></b> === | ||
| − | Vi ställer frågan efter kurvan <math> \, y = f\,(x)</math>:s lutning i en given punkt <math> \, x = a \, </math>, som är identisk med < | + | Vi ställer frågan efter kurvan <math> \, y = f\,(x)</math>:s lutning i en given punkt <math> \, x = a \, </math>, som är identisk med <b><span style="color:red">tangentens lutning</span></b> i denna punkt. Med denna lutning samt punkten <math> \, (a,\,f(a)) \, </math> kan vi ställa upp tangentens ekvation. Men hur får vi tangentens lutning? |
Tangentens lutning får vi genom att först beräkna sekantens lutning och sedan låta sekanten gå över till tangenten. | Tangentens lutning får vi genom att först beräkna sekantens lutning och sedan låta sekanten gå över till tangenten. | ||
| Rad 199: | Rad 199: | ||
| − | Se [[2.1 Lösning till Aktiviteten Introduktion till derivata|< | + | Se [[2.1 Lösning till Aktiviteten Introduktion till derivata|<b><span style="color:blue">Lösning till Aktiviteten Introduktion till derivata</span></b>]], ''Geometrisk tolkning''. |
| Rad 222: | Rad 222: | ||
| − | [[Matte:Copyrights|Copyright]] © 2011- | + | [[Matte:Copyrights|Copyright]] © 2011-2016 Taifun Alishenas. All Rights Reserved. |
Versionen från 10 oktober 2016 kl. 13.36
| \( \pmb{\gets} \) Förra avsnitt | Genomgång | Övningar | Nästa avsnitt \( \pmb{\to} \) |
Lektion 19 Derivatans definition I
Lektion 20 Derivatans definition II
Derivatan i en punkt
Exempel Oljetank
| En oljetank läcker genom ett hål i tankens botten (Exempel 3 i förra avsnitt).
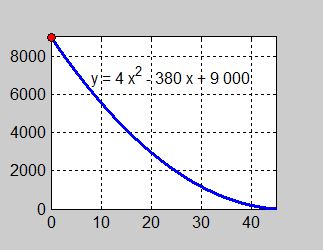
Oljans utströmning beskrivs av funktionen:
där \( \quad\; x \, = \, {\rm Tiden\;i\;minuter} \)
a) Beräkna oljans genomsnittliga utströmningshastighet i intervallet \( \, 0 \,\leq\, x \,\leq\, h \quad \) \( \;\;\, \) som ett uttryck i \( \, h > 0 \, \) (något positivt tal). b) Beräkna oljans momentana utströmningshastighet i punkten \( \, x = 0 \) genom att \( \;\;\, \) i uttrycket från a) låta \( \, h \, \) gå mot \( \, 0 \). |
 |
Lösning:
a) Den allmänna definitionen av genomsnittlig förändringshastighet är:
- \[ {\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h} \qquad {\rm i\;\;intervallet } \qquad x_1 \,\leq\, x \,\leq\, x_1 + h \]
I exemplet Oljetank är \( \,x_1 = 0 \). Då har vi:
- \[ {\Delta y \over \Delta x} \; = \; {f(0 + h) \, - \, f(0) \over h} \; = \; {f(h) \, - \, f(0) \over h} \qquad {\rm i\;\;intervallet } \qquad 0 \,\leq\, x \,\leq\, h \]
För \( \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, \) får vi \( \, f\,(h) \, = \, 4\,h^2 - 380\,h + 9\,000 \, \) och \( \, f\,(0) \, = \, 9\,000 \).
Då blir oljans genomsnittliga utströmningshastighet i intervallet \( 0 \,\leq\, x \,\leq\, h \, \):
- \[ {\Delta y \over \Delta x} \,=\, {f(h) \, - \, f(0) \over h} \,=\, {4\,h^2 - 380\,h + 9\,000 \,-\, 9\,000 \over h} \,=\, {4\,h^2 - 380\,h \over h} \,=\, {{\color{Red} h}\,(4\,h - 380) \over {\color{Red} h}} \,=\, 4\,h - 380 \]
b) Nu låter vi i uttrycket \( 4\,h - 380 \) för den genomsnittliga utströmningshastigheten \( \, h\, \) gå mot \( 0\, \) för att få oljans momentana utströmningshastighet i \( \, x = 0\, \).
Dvs vi beräknar gränsvärdet:
- \[ \qquad \displaystyle \lim_{h \to 0}\, {(4\,h - 380)} \,=\, -\,380 \]
\( -\,380\, \) är oljans momentana utströmningshastighet i \( \, x = 0 \, \). Dvs vid denna tidpunkt sjunker oljan med exakt \( 380\, \) liter per minut.
Ett annat ord för den momentana utströmningshastigheten är derivatan:
Funktionen \( \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, \) har i punkten \( \, x = 0 \; \) derivatan \( \; -\,380 \; \).
Man skriver: \( \; f\,{\color{Red} '}(0) \,=\, -\,380 \; \) och läser: "\( \, f \) prim av \( \, 0 \, \) är \( \; -\,380 \; \)" .
Vi fick derivatan av \( \, f(x) \, \) i punkten \( \, x = 0\, \) genom att först (a) ställa upp den genomsnittliga förändringshastigheten i intervallet \( \, 0 \,\leq\, x \,\leq\, h \, \) som ett uttryck i \( \, h \, \) och sedan (b) beräkna uttryckets gränsvärde för \( \, h \to 0 \). Det blev talet \( \, -\,380 \).
Derivatan som ett tal
Derivatan som en funktion
Exemplet ovan visar att derivatan av en andragradsfunktion (parabel) är en linjär funktion (rät linje).
Medan vi i Exemplet Oljetank beräknade derivatan i en punkt som ett tal, anger exemplet ovan derivatan som en ny funktion. Hur kommer denna nya syn på derivatan till?
Den nya derivatfunktionen får man genom att betrakta punkten \( \, a \, \) inte längre som en konstant utan som en variabel \( \, x \). Med andra ord, man tillämpar definitionen av derivatan i en punkt på varenda punkt \( \, a \, \) på \( \, x\)-axeln. Tänker man sig att alla dessa derivatvärden är tilldelade sina respektive \( \, x\)-värden, bildar denna tilldelning en ny funktion som är den ursprungliga funktionens derivata, fast inte längre som ett tal utan som ett uttryck i \( \, x \).
Derivatans allmänna definition
Derivatan av funktionen \( \, y = f\,(x) \, \) är \( \, \displaystyle f\,\,{\color{Red} '}\,\,(x) \; = \; \lim_{h \to 0}\,\,{f(x + h) \, - \, f(x) \over h} \)
\( {\color{Red} '} \; \) är symbolen för derivatan. \( \;\, f\,{\color{Red} '}(x) \; \) läses så här: "\( \, f \) prim av \( \, x \, \)" .
Som man ser är uttrycket i limes funktionens genomsnittliga förändringshastighet \( \, \displaystyle{\Delta y \over \Delta x} \, \) i intervallet mellan \( \, x \, \) och \( \, h \). Dvs \( \, \displaystyle f\,'(x) \, = \, \lim_{\Delta x \to 0}\,\,{\Delta y \over \Delta x} \).
Exempel Oljetank (utvidgat)
Utströmningen av olja genom ett hål i oljetankens botten beskrivs av funktionen:
- \[ y \, = \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \]
a) Ställ upp funktionens genomsnittliga förändringshastighet \( \, \displaystyle{\Delta y \over \Delta x} \, \) som ett uttryck i \( \, x \, \) och \( \, h \).
b) Ange derivatan av \( \, f\,(x) \, \) som en ny funktion av \( \, x \, \) genom att i \( \, \displaystyle{\Delta y \over \Delta x} \, \) låta \( \, h \, \) gå mot \( \, 0 \).
\( \;\;\, \) Rita grafen till derivatans funktion
Lösning:
a) Vi ställer upp de deluttryck som ingår i \( \, \displaystyle{\Delta y \over \Delta x} \, = \, {f(x + h) \, - \, f(x) \over h} \, \) och förenklar dem:
\[ \begin{array}{lcl} f(x + h) & = & 4\,(x+h)^2 - 380\,(x+h) + 9\,000 = 4\,(x^2 + 2\,x\,h + h^2) - 380\,x - 380\,h + 9\,000 = \\ & = & 4\,x^2 + 8\,x\,h + 4\,h^2 - 380\,x - 380\,h + 9\,000 \\ f(x + h) - f(x) & = & 4\,x^2 + 8\,x\,h + 4\,h^2 - 380\,x - 380\,h + 9\,000 - (4\,x^2 - 380\,x + 9\,000) = \\ & = & 4\,x^2 + 8\,x\,h + 4\,h^2 - 380\,x - 380\,h + 9\,000 - 4\,x^2 + 380\,x - 9\,000 \;\;\, =\\ & = & 8\,x\,h + 4\,h^2 - 380\,h \, = \, h\,(8\,x + 4\,h - 380) \\ {f(x + h) - f(x) \over h} & = & {h\,(8\,x + 4\,h - 380) \over h} \, = \, 8\,x + 4\,h - 380 \end{array}\]
b) Nu beräknar vi gränsvärdet:
Vi kan sammanfatta: Funktionen \( \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, \) har derivatan \( \; f\,'\,(x) = 8\,x - 380 \; \). Grafen till derivatans funktion visas till höger. |
Fil:Oljetank derivataa.jpg |
I efterhand kan vi nu verifiera det i Exempel Oljetank beräknade värdet av \( f\,(x)\):s derivata i punkten \( \, x = 0 \) genom att sätta in \( \, x = 0 \) i derivatans funktion \( f\,'\,(x) = 8\,x - 380 \):
- \[ f\,'\,(0) \,=\, 8 \cdot 0 - 380 \,=\, 0 - 380 \,=\, -\,380 \]
Vid tiden \( \, x = 0 \, \) sjönk oljan med \( \, 380\, \) liter per minut som var den största utströmningshastigheten när oljan hade mest volym och utövade det största trycket på hålet.
Tidigare (Exempel 3 d) hade vi fått \( -\,379,6\, \) för den genomsnittliga utströmningshastighet i intervallet \( 0 \,\leq\, x \,\leq\, 0,1 \), vilket är ett närmevärde för derivatan, som nu visar sig vara ganska bra. Närmevärdet hade blivit ännu precisare om vi hade valt t.ex. intervallet \( 0 \,\leq\, x \,\leq\, 0,01 \) eller \( 0 \,\leq\, x \,\leq\, 0,001 \) osv. Det exakta värdet \( -\,380 \, \) får man om man i intervallet \( 0 \,\leq\, x \,\leq\, h \) låter \( h \to 0 \).
Dessutom får vi genom grafen ovan för tredje gången en bekräftelse på följande sats som kommer att bevisas generellt senare:
Det första exemplet på denna sats hade vi sett i kapitlets inledande Aktivitet (Lösning, punkt 6) då vi ritade grafen till hastighetsfunktionen till Yulias hopp från 10 m-torn. Det andra var när vi i detta avsnitt i Derivatan som en funktion såg grafen till derivatan \( \, y\,' = \, 10\,x \, \) av funktionen \( \, y \, = \, 5\,x^2 \, \).
I hela exemplet Oljetank är oljans momentana utströmningshastighet derivatans fysikaliska tolkning.
Men derivatan har även en geometrisk tolkning som är ganska intuitiv:
Från sekanten till tangenten
Vi ställer frågan efter kurvan \( \, y = f\,(x)\):s lutning i en given punkt \( \, x = a \, \), som är identisk med tangentens lutning i denna punkt. Med denna lutning samt punkten \( \, (a,\,f(a)) \, \) kan vi ställa upp tangentens ekvation. Men hur får vi tangentens lutning?
Tangentens lutning får vi genom att först beräkna sekantens lutning och sedan låta sekanten gå över till tangenten.
Ekvation för tangenten till en kurva
Se Lösning till Aktiviteten Introduktion till derivata, Geometrisk tolkning.
Internetlänkar
http://www.youtube.com/watch?v=OyKmc2bPWe0
http://www.youtube.com/watch?v=8of_svLfcjk
http://www.youtube.com/watch?v=OY8CeLUxE64&feature=related
http://www.youtube.com/watch?v=2wH-g60EJ18&feature=related
http://www.larcentrum.org/Safir/MA1203W/htm/m03_deriv1/m03_deriv_definition.htm
http://www.naturvetenskap.org/index.php?option=com_content&view=article&id=129&Itemid=132
Copyright © 2011-2016 Taifun Alishenas. All Rights Reserved.