Skillnad mellan versioner av "3.5 Övningar till Extremvärdesproblem"

Från Mathonline
Hoppa till: navigering, sök
m (→‎Övning 9)
m
 
(39 mellanliggande versioner av samma användare visas inte)
Rad 2: Rad 2:
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
−
{{Not selected tab|[[3.4 Kurvkonstruktioner|<-- Förra avsnitt]]}}
+
{{Not selected tab|[[3.4 Kurvkonstruktioner| <<&nbsp;&nbsp;Förra avsnitt]]}}
 
{{Not selected tab|[[3.5 Extremvärdesproblem|Genomgång]]}}
 
{{Not selected tab|[[3.5 Extremvärdesproblem|Genomgång]]}}
 
{{Selected tab|[[3.5 Övningar till Extremvärdesproblem|Övningar]]}}
 
{{Selected tab|[[3.5 Övningar till Extremvärdesproblem|Övningar]]}}
−
{{Not selected tab|[[Denna sida ingår inte i demon.|<span style="color:red">Diagnosprov kap 3 Anv. av deriv.</span>]]}}
+
{{Not selected tab|[[Diagnosprov kap 3 Användning av derivata|Diagnosprov kap 3 Anv. av deriv.]]}}
−
<!-- {{Not selected tab|[[Diagnosprov kap 3 Användning av derivata|Diagnosprov kap 3 Anv. av deriv.]]}} -->
+
{{Not selected tab|[[Lösningar till diagnosprov kap 3 Användning av derivata|Lösningar till diagnosprov kap 3]]}}
−
{{Not selected tab|[[Denna sida ingår inte i demon.|<span style="color:red">Lösningar till diagnosprov kap 3</span>]]}}
+
−
<!-- {{Not selected tab|[[Lösningar till diagnosprov kap 3 Användning av derivata|Lösningar till diagnosprov kap 3]]}} -->
+
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
  
  
 +
<Big><Big><Big><span style="color:#FFB69C">E-övningar: 1-5</span></Big></Big></Big>
  
−
<Big><Big><Big><span style="color:blue">E-övningar: 1-5</span></Big></Big></Big>
 
  
−
 
+
== <b>Övning 1</b> ==
−
== Övning 1 ==
+
<div class="ovnE">
−
<div class="ovning">
+
 
<table>
 
<table>
 
<tr>
 
<tr>
Rad 27: Rad 24:
 
Vilken position av <math> \, P \, (x, \, y) \, </math> ger maximal area till den skuggade rektangeln?
 
Vilken position av <math> \, P \, (x, \, y) \, </math> ger maximal area till den skuggade rektangeln?
  
 +
a) &nbsp; Vad är problemets [[3.5_Extremvärdesproblem#Bivillkor_f.C3.B6r_ett_extremv.C3.A4rdesproblem|<strong><span style="color:blue">bivillkor</span></strong>]]?
  
−
a) &nbsp; Vad är problemets [[3.5_Extremvärdesproblem#Exempel_1_Rektangel_i_parabel|<strong><span style="color:blue">bivillkor</span></strong>]]?
+
b) &nbsp; Ställ upp problemets [[3.5_Extremvärdesproblem#M.C3.A5lfunktion_f.C3.B6r_ett_extremv.C3.A4rdesproblem|<strong><span style="color:blue">målfunktion</span></strong>]] som en funktion av endast en variabel.
−
 
+
−
b) &nbsp; Ställ upp problemets [[3.5_Extremvärdesproblem#Exempel_1_Rektangel_i_parabel|<strong><span style="color:blue">målfunktion</span></strong>]] som en funktion av endast en variabel.
+
  
 
c) &nbsp; Bestäm koordinaterna till <math> \, P \, </math> så att rektangelns area blir maximal.
 
c) &nbsp; Bestäm koordinaterna till <math> \, P \, </math> så att rektangelns area blir maximal.
Rad 40: Rad 36:
 
</tr>
 
</tr>
 
</table>
 
</table>
−
</div>{{#NAVCONTENT:Svar 1a|3.5 Svar 1a|Svar 1b|3.5 Svar 1b|Lösning 1b|3.5 Lösning 1b|Svar 1c|3.5 Svar 1c|Lösning 1c|3.5 Lösning 1c|Svar 1d|3.5 Svar 1d|Lösning 1d|3.5 Lösning 1d}}
+
{{#NAVCONTENT:Svar 1a|3.5 Svar 1a|Svar 1b|3.5 Svar 1b|Lösning 1b|3.5 Lösning 1b|Svar 1c|3.5 Svar 1c|Lösning 1c|3.5 Lösning 1c|Svar 1d|3.5 Svar 1d|Lösning 1d|3.5 Lösning 1d}}</div>
  
−
== Övning 2 ==
+
 
−
<div class="ovning">
+
== <b>Övning 2</b> ==
 +
<div class="ovnE">
 
<table>
 
<table>
 
<tr>
 
<tr>
 
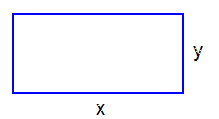
   <td>En rektangel har omkretsen <math> \, 12 \, {\rm  cm} \, </math>. Maximera rektangelns area.
 
   <td>En rektangel har omkretsen <math> \, 12 \, {\rm  cm} \, </math>. Maximera rektangelns area.
−
 
  
 
a) &nbsp; Formulera problemets bivillkor.
 
a) &nbsp; Formulera problemets bivillkor.
Rad 58: Rad 54:
 
</td>
 
</td>
 
   <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image: Ovn 352.gif]]
 
   <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image: Ovn 352.gif]]
−
 
−
 
 
</td>
 
</td>
 
</tr>
 
</tr>
 
</table>
 
</table>
−
</div>{{#NAVCONTENT:Svar 2a|3.5 Svar 2a|Lösning 2a|3.5 Lösning 2a|Svar 2b|3.5 Svar 2b|Lösning 2b|3.5 Lösning 2b|Svar 2c|3.5 Svar 2c|Lösning 2c|3.5 Lösning 2c|Svar 2d|3.5 Svar 2d}}
+
{{#NAVCONTENT:Svar 2a|3.5 Svar 2a|Lösning 2a|3.5 Lösning 2a|Svar 2b|3.5 Svar 2b|Lösning 2b|3.5 Lösning 2b|Svar 2c|3.5 Svar 2c|Lösning 2c|3.5 Lösning 2c|Svar 2d|3.5 Svar 2d}}</div>
  
−
== Övning 3 ==
+
 
−
<div class="ovning">
+
== <b>Övning 3</b> ==
 +
<div class="ovnE">
 
<table>
 
<table>
 
<tr>
 
<tr>
 
   <td>En rektangels area är <math> \, 25 \, {\rm  cm}^2 \, </math>. Minimera rektangelns omkrets.
 
   <td>En rektangels area är <math> \, 25 \, {\rm  cm}^2 \, </math>. Minimera rektangelns omkrets.
−
 
  
 
a) &nbsp; Formulera problemets bivillkor.
 
a) &nbsp; Formulera problemets bivillkor.
Rad 81: Rad 75:
 
</td>
 
</td>
 
   <td>&nbsp;&nbsp; [[Image: Ovn 352.gif]]
 
   <td>&nbsp;&nbsp; [[Image: Ovn 352.gif]]
−
 
−
 
 
</td>
 
</td>
 
</tr>
 
</tr>
 
</table>
 
</table>
−
</div>{{#NAVCONTENT:Svar 3a|3.5 Svar 3a|Lösning 3a|3.5 Lösning 3a|Svar 3b|3.5 Svar 3b|Lösning 3b|3.5 Lösning 3b|Svar 3c|3.5 Svar 3c|Lösning 3c|3.5 Lösning 3c|Svar 3d|3.5 Svar 3d}}
+
{{#NAVCONTENT:Svar 3a|3.5 Svar 3a|Lösning 3a|3.5 Lösning 3a|Svar 3b|3.5 Svar 3b|Lösning 3b|3.5 Lösning 3b|Svar 3c|3.5 Svar 3c|Lösning 3c|3.5 Lösning 3c|Svar 3d|3.5 Svar 3d}}</div>
  
−
== Övning 4 ==
+
 
−
<div class="ovning">
+
== <b>Övning 4</b> ==
 +
<div class="ovnE">
 
<table>
 
<table>
 
<tr>
 
<tr>
Rad 101: Rad 94:
  
 
Vilken position av <math> \, P \, </math> ger triangeln största möjliga arean <math> \, A \, </math>?
 
Vilken position av <math> \, P \, </math> ger triangeln största möjliga arean <math> \, A \, </math>?
−
 
  
 
a) &nbsp; Ange problemets bivillkor.  
 
a) &nbsp; Ange problemets bivillkor.  
Rad 117: Rad 109:
 
</table>
 
</table>
  
−
</div>{{#NAVCONTENT:Svar 4a|3.5 Svar 4a|Svar 4b|3.5 Svar 4b|Lösning 4b|3.5 Lösning 4b|Svar 4c|3.5 Svar 4c|Lösning 4c|3.5 Lösning 4c|Svar 4d|3.5 Svar 4d|Lösning 4d|3.5 Lösning 4d}}
+
{{#NAVCONTENT:Svar 4a|3.5 Svar 4a|Svar 4b|3.5 Svar 4b|Lösning 4b|3.5 Lösning 4b|Svar 4c|3.5 Svar 4c|Lösning 4c|3.5 Lösning 4c|Svar 4d|3.5 Svar 4d|Lösning 4d|3.5 Lösning 4d}}</div>
  
−
== Övning 5 ==
+
 
−
<div class="ovning">
+
== <b>Övning 5</b> ==
 +
<div class="ovnE">
 
<table>
 
<table>
 
<tr>
 
<tr>
−
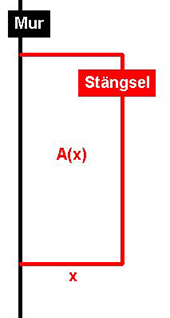
   <td>En fårherde vill samla sina får under en sommarnatt vid en mur i ett rektan-
+
   <td>En fårherde vill samla sina får vid en mur i ett rektangulärt stängsel.
  
−
gulärt område som hon/han avgränsar med hjälp av ett rep på <math> \, 9 \; {\rm m} \, </math> (rött)
+
Hon/han avgränsar stängslet med ett rep och pinnar i marken enligt
  
−
och pinnar i marken enligt figuren.
+
figuren. Repet är <math> \, 9 \; {\rm m} \, </math> långt (rött).  
  
−
Hur ska fårherden välja stängselns mått för att få den största möjliga ytan för
+
Beteckna rektangelns kortare sida med <math> \, x </math>. Hur ska fårherden välja
  
−
sina får?
+
stängslets mått för att få den störst möjliga arean <math> \, A \, </math> för sina får?
  
  
−
a) &nbsp; Formulera problemets målfunktion <math> \, A(x) \, </math>.
+
a) &nbsp; Skriv <math> \, A \, </math> som en funktion av <math> \, x </math>, problemets målfunktion <math> \, A(x) \, </math>.
  
 
b) &nbsp; Ange målfunktionens definitionsmängd.
 
b) &nbsp; Ange målfunktionens definitionsmängd.
  
−
c) &nbsp; Bestäm <math> \, x \, </math> så att stängselns area blir maximal.  
+
c) &nbsp; Bestäm <math> \, x \, </math> så att stängslets area blir maximal.  
  
−
d) &nbsp; Beräkna stängselns maximala area.
+
d) &nbsp; Beräkna stängslets maximala area.
  
 
e) &nbsp; Har problemet ett bivillkor? Om ja, ange det.
 
e) &nbsp; Har problemet ett bivillkor? Om ja, ange det.
  
−
f) &nbsp; Kan du intuitivt komma på andra geometriska figurer än rektangeln som
+
<!-- f) &nbsp; Kan du intuitivt komma på andra geometriska figurer än rektan-
−
 
+
−
:skulle kunna maximera stängselns area bättre?
+
  
 +
&nbsp;&nbsp;&nbsp;&nbsp; geln som skulle kunna maximera stängslets area bättre?
 +
-->
 
</td>
 
</td>
 
   <td>&nbsp;&nbsp;&nbsp; [[Image: Ovn 355_80.jpg]]
 
   <td>&nbsp;&nbsp;&nbsp; [[Image: Ovn 355_80.jpg]]
Rad 155: Rad 148:
 
</table>
 
</table>
  
−
</div>{{#NAVCONTENT:Svar 5a|3.5 Svar 5a|Lösning 5a|3.5 Lösning 5a|Svar 5b|3.5 Svar 5b|Svar 5c|3.5 Svar 5c|Lösning 5c|3.5 Lösning 5c|Svar 5d|3.5 Svar 5d|Lösning 5d|3.5 Lösning 5d|Svar 5e|3.5 Svar 5e|Lösning 5e|3.5 Lösning 5e|Svar 5f|3.5 Svar 5f}}
+
<!-- {{#NAVCONTENT:Svar 5a|3.5 Svar 5a|Lösning 5a|3.5 Lösning 5a|Svar 5b|3.5 Svar 5b|Svar 5c|3.5 Svar 5c|Lösning 5c|3.5 Lösning 5c|Svar 5d|3.5 Svar 5d|Lösning 5d|3.5 Lösning 5d|Svar 5e|3.5 Svar 5e|Lösning 5e|3.5 Lösning 5e|Svar 5f|3.5 Svar 5f}}</div> -->
 +
{{#NAVCONTENT:Svar 5a|3.5 Svar 5a|Lösning 5a|3.5 Lösning 5a|Svar 5b|3.5 Svar 5b|Svar 5c|3.5 Svar 5c|Lösning 5c|3.5 Lösning 5c|Svar 5d|3.5 Svar 5d|Lösning 5d|3.5 Lösning 5d|Svar 5e|3.5 Svar 5e|Lösning 5e|3.5 Lösning 5e}}</div>
  
  
−
<Big><Big><Big><span style="color:blue">C-övningar: 6-7</span></Big></Big></Big>
 
  
  
−
== Övning 6 ==
+
<Big><Big><Big><span style="color:#86B404">C-övningar: 6-7</span></Big></Big></Big>
−
<div class="ovning">
+
 
 +
 
 +
== <b>Övning 6</b> ==
 +
<div class="ovnC">
 
<table>
 
<table>
 
<tr>
 
<tr>
Rad 174: Rad 170:
  
 
öppna låda?
 
öppna låda?
−
 
  
 
a) &nbsp; Inför en ny beteckning och ange problemets bivillkor, se [[3.5_Lösning_5e|<strong><span style="color:blue">Lösning 5 e)</span></strong>]].
 
a) &nbsp; Inför en ny beteckning och ange problemets bivillkor, se [[3.5_Lösning_5e|<strong><span style="color:blue">Lösning 5 e)</span></strong>]].
Rad 197: Rad 192:
 
</table>
 
</table>
  
−
</div>{{#NAVCONTENT:Svar 6a|3.5 Svar 6a|Lösning 6a|3.5 Lösning 6a|Svar 6b|3.5 Svar 6b|Lösning 6b|3.5 Lösning 6b|Svar 6c|3.5 Svar 6c|Lösning 6c|3.5 Lösning 6c|Svar 6d|3.5 Svar 6d|Lösning 6d|3.5 Lösning 6d|Svar 6e|3.5 Svar 6e|Lösning 6e|3.5 Lösning 6e|Svar 6f|3.5 Svar 6f|Lösning 6f|3.5 Lösning 6f}}
+
{{#NAVCONTENT:Svar 6a|3.5 Svar 6a|Lösning 6a|3.5 Lösning 6a|Svar 6b|3.5 Svar 6b|Lösning 6b|3.5 Lösning 6b|Svar 6c|3.5 Svar 6c|Lösning 6c|3.5 Lösning 6c|Svar 6d|3.5 Svar 6d|Lösning 6d|3.5 Lösning 6d|Svar 6e|3.5 Svar 6e|Lösning 6e|3.5 Lösning 6e|Svar 6f|3.5 Svar 6f|Lösning 6f|3.5 Lösning 6f}}</div>
  
−
== Övning 7 ==
+
 
−
<div class="ovning">
+
== <b>Övning 7</b> ==
 +
<div class="ovnC">
 
SJ har <math> \, 20\,000 \, </math> passagerare per månad på en viss bansträcka med ett biljettpris på <math> \, 200 \, </math> kr.
 
SJ har <math> \, 20\,000 \, </math> passagerare per månad på en viss bansträcka med ett biljettpris på <math> \, 200 \, </math> kr.
  
−
En marknadsundersökning visar att varje höjning av biljettpriset med <math> \, 1 \, </math> kr skulle medföra en förlust av <math> \, 80 \, </math> passagerare per månad.
+
En marknadsundersökning visar att varje höjning av biljettpriset med <math> \, 1 \, </math> kr skulle medföra
 +
 
 +
en förlust av <math> \, 80 \, </math> passagerare per månad.
  
 
Vilken biljettprishöjning kommer att maximera intäkten per månad?
 
Vilken biljettprishöjning kommer att maximera intäkten per månad?
  
 +
a) &nbsp; Ange problemets [[3.5_Extremvärdesproblem#Bivillkor_f.C3.B6r_ett_extremv.C3.A4rdesproblem|<strong><span style="color:blue">bivillkor</span></strong>]] om
  
−
a) &nbsp; Ange problemets bivillkor om:
+
<math> \qquad\;\; x \, = \, </math> Den planerade prishöjningen i kr.
  
−
:::<math> x \, = \, {\rm Den\;planerade\;prishöjningen\;i\;kr.} </math>
+
<math> \qquad\;\; y \, = \,  </math> Antalet passagerare per månad efter prishöjningen <math> \, x \, </math>.
  
−
:::<math> y \, = \, {\rm Antalet\;passagerare\;per\;månad\;efter\;en\;sådan\;prishöjning.} </math>
+
b) &nbsp; Ställ upp problemets [[3.5_Extremvärdesproblem#M.C3.A5lfunktion_f.C3.B6r_ett_extremv.C3.A4rdesproblem|<strong><span style="color:blue">målfunktion</span></strong>]] <math> \, I(x) \, </math> för SJ:s intäkt per månad.
−
 
+
−
b) &nbsp; Ställ upp problemets målfunktionen <math> \, I(x) \, </math> för SJ:s intäkt per månad.
+
  
 
c) &nbsp; Bestäm <math> \, x \, </math> så att intäkten <math> \, I(x) \, </math> blir så stor som möjligt.
 
c) &nbsp; Bestäm <math> \, x \, </math> så att intäkten <math> \, I(x) \, </math> blir så stor som möjligt.
Rad 221: Rad 218:
  
 
e) &nbsp; För vilka prishöjningar kommer det inte längre att löna sig att höja biljettpriset?
 
e) &nbsp; För vilka prishöjningar kommer det inte längre att löna sig att höja biljettpriset?
−
</div>{{#NAVCONTENT:Svar 7a|3.5 Svar 7a|Lösning 7a|3.5 Lösning 7a|Svar 7b|3.5 Svar 7b|Lösning 7b|3.5 Lösning 7b|Svar 7c|3.5 Svar 7c|Lösning 7c|3.5 Lösning 7c|Svar 7d|3.5 Svar 7d|Lösning 7d|3.5 Lösning 7d|Svar 7e|3.5 Svar 7e|Lösning 7e|3.5 Lösning 7e}}
+
{{#NAVCONTENT:Svar 7a|3.5 Svar 7a|Lösning 7a|3.5 Lösning 7a|Svar 7b|3.5 Svar 7b|Lösning 7b|3.5 Lösning 7b|Svar 7c|3.5 Svar 7c|Lösning 7c|3.5 Lösning 7c|Svar 7d|3.5 Svar 7d|Lösning 7d|3.5 Lösning 7d|Svar 7e|3.5 Svar 7e|Lösning 7e|3.5 Lösning 7e}}</div>
  
  
−
<Big><Big><Big><span style="color:blue">A-övningar: 8-9</span></Big></Big></Big>
 
  
  
−
== Övning 8 ==
+
<Big><Big><Big><span style="color:#62D9FD">A-övningar: 8-9</span></Big></Big></Big>
−
<div class="ovning">
+
 
 +
 
 +
== <b>Övning 8</b> ==
 +
<div class="ovnA">
 
<table>
 
<table>
 
<tr>
 
<tr>
Rad 238: Rad 237:
  
 
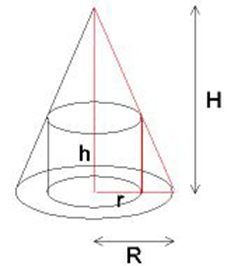
Vilka mått på cylindern maximerar dess volym <math> \, V \, </math>?
 
Vilka mått på cylindern maximerar dess volym <math> \, V \, </math>?
−
 
  
 
a) &nbsp; Formulera problemets bivillkor. Använd den röda triangeln i figuren.  
 
a) &nbsp; Formulera problemets bivillkor. Använd den röda triangeln i figuren.  
Rad 256: Rad 254:
 
</tr>
 
</tr>
 
</table>
 
</table>
−
</div>{{#NAVCONTENT:Svar 8a|3.5 Svar 8a|Lösning 8a|3.5 Lösning 8a|Svar 8b|3.5 Svar 8b|Lösning 8b|3.5 Lösning 8b|Svar 8c|3.5 Svar 8c|Lösning 8c|3.5 Lösning 8c|Svar 8d|3.5 Svar 8d|Lösning 8d|3.5 Lösning 8d|Svar 8e|3.5 Svar 8e|Lösning 8e|3.5 Lösning 8e}}
+
{{#NAVCONTENT:Svar 8a|3.5 Svar 8a|Lösning 8a|3.5 Lösning 8a|Svar 8b|3.5 Svar 8b|Lösning 8b|3.5 Lösning 8b|Svar 8c|3.5 Svar 8c|Lösning 8c|3.5 Lösning 8c|Svar 8d|3.5 Svar 8d|Lösning 8d|3.5 Lösning 8d|Svar 8e|3.5 Svar 8e|Lösning 8e|3.5 Lösning 8e}}</div>
  
−
== Övning 9 ==
+
 
−
<div class="ovning">
+
== <b>Övning 9</b> ==
 +
<div class="ovnA">
 
<table>
 
<table>
 
<tr>
 
<tr>
Rad 266: Rad 265:
 
plåt till förfogande (efter spill). Dvs cylinderns begränsningsarea <math> \, = \, A \; {\rm cm}^2 \, </math>.
 
plåt till förfogande (efter spill). Dvs cylinderns begränsningsarea <math> \, = \, A \; {\rm cm}^2 \, </math>.
  
−
I teoridelen, [[3.5_Extremvärdesproblem#Exempel_3_Konservburk|<strong><span style="color:blue">Exempel 3 Konservburk</span></strong>]], löstes denna uppgift med <math>A=500</math>.
+
I genomgången, [[3.5_Extremvärdesproblem#Exempel_3_Konservburk|<strong><span style="color:blue">Exempel 3 Konservburk</span></strong>]], löstes denna uppgift för <math> \, A = 500 </math>.
  
−
Här ska den lösas generellt för en given konstant <math> \, A \, </math>.
+
Här ska du lösa den generellt för en given konstant <math> \, A \, </math>.
  
 
Vilka mått på konserven maximerar volymen?
 
Vilka mått på konserven maximerar volymen?
−
 
  
 
a) &nbsp; Formulera problemets bivillkor.
 
a) &nbsp; Formulera problemets bivillkor.
Rad 291: Rad 289:
 
:::::::::<math> 2 \; r \; = \; h </math>
 
:::::::::<math> 2 \; r \; = \; h </math>
  
−
</div>{{#NAVCONTENT:Svar 9a|3.5 Svar 9a|Lösning 9a|3.5 Lösning 9a|Svar 9b|3.5 Svar 9b|Lösning 9b|3.5 Lösning 9b|Svar 9c|3.5 Svar 9c|Lösning 9c|3.5 Lösning 9c|Svar 9d|3.5 Svar 9d|Lösning 9d|3.5 Lösning 9d}}
+
{{#NAVCONTENT:Svar 9a|3.5 Svar 9a|Lösning 9a|3.5 Lösning 9a|Svar 9b|3.5 Svar 9b|Lösning 9b|3.5 Lösning 9b|Svar 9c|3.5 Svar 9c|Lösning 9c|3.5 Lösning 9c|Svar 9d|3.5 Svar 9d|Lösning 9d|3.5 Lösning 9d}}</div>
  
  
Rad 300: Rad 298:
  
  
−
[[Matte:Copyrights|Copyright]] © 2011-2015 Taifun Alishenas. All Rights Reserved.
+
[[Matte:Copyrights|Copyright]] © 2011-2016 Math Online Sweden AB. All Rights Reserved.

Nuvarande version från 24 januari 2019 kl. 10.52

        <<  Förra avsnitt          Genomgång          Övningar          Diagnosprov kap 3 Anv. av deriv.          Lösningar till diagnosprov kap 3      


E-övningar: 1-5


Övning 1

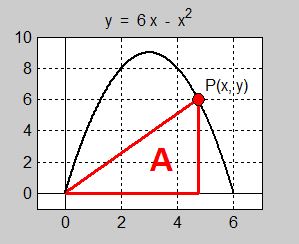
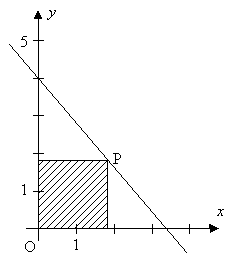
I figuren till höger rör sig punkten \( \, P \, \) på den räta linje vars ekvation är:
\[ y = -\,{6 \over 5}\,x + 4 \]

Vilken position av \( \, P \, (x, \, y) \, \) ger maximal area till den skuggade rektangeln?

a)   Vad är problemets bivillkor?

b)   Ställ upp problemets målfunktion som en funktion av endast en variabel.

c)   Bestäm koordinaterna till \( \, P \, \) så att rektangelns area blir maximal.

d)   Beräkna rektangelns maximala area.

  Ovn 351.gif
Svar 1a
3.5 Svar 1a
Svar 1b
3.5 Svar 1b
Lösning 1b
3.5 Lösning 1b
Svar 1c
3.5 Svar 1c
Lösning 1c
3.5 Lösning 1c
Svar 1d
3.5 Svar 1d
Lösning 1d
3.5 Lösning 1d


Övning 2

En rektangel har omkretsen \( \, 12 \, {\rm cm} \, \). Maximera rektangelns area.

a)   Formulera problemets bivillkor.

b)   Ange problemets målfunktion.

c)   Bestäm sidorna \( \, x \, \) och \( \, y \, \) så att rektangelns area blir maximal.

d)   Vad blir rektangelns maximala area?

        Ovn 352.gif
Svar 2a
3.5 Svar 2a
Lösning 2a
3.5 Lösning 2a
Svar 2b
3.5 Svar 2b
Lösning 2b
3.5 Lösning 2b
Svar 2c
3.5 Svar 2c
Lösning 2c
3.5 Lösning 2c
Svar 2d
3.5 Svar 2d


Övning 3

En rektangels area är \( \, 25 \, {\rm cm}^2 \, \). Minimera rektangelns omkrets.

a)   Formulera problemets bivillkor.

b)   Ange problemets målfunktion.

c)   Bestäm sidorna \( \, x \, \) och \( \, y \, \) så att rektangelns omkrets blir minimal.

d)   Vad blir rektangelns minimala omkrets?

   Ovn 352.gif
Svar 3a
3.5 Svar 3a
Lösning 3a
3.5 Lösning 3a
Svar 3b
3.5 Svar 3b
Lösning 3b
3.5 Lösning 3b
Svar 3c
3.5 Svar 3c
Lösning 3c
3.5 Lösning 3c
Svar 3d
3.5 Svar 3d


Övning 4

En rätvinklig triangel är inbunden i en parabel enligt figuren:

Parabeln är definierad genom:

\[ y \, = \, 6 \, x \, - \, x^2 \qquad {\rm med} \qquad 0 \, \leq \, x \, \leq \, 6 \]

Punkten \( \, P\,(x,\,y) \, \) rör sig på parabeln.

Vilken position av \( \, P \, \) ger triangeln största möjliga arean \( \, A \, \)?

a)   Ange problemets bivillkor.

b)   Ställ upp problemets målfunktion som en funktion \( \, A(x) \, \).

c)   Bestäm koordinaterna till \( \, P \, \) så att triangelns area blir maximal.

d)   Beräkna triangelns maximala area.

       Ovn 354.jpg
Svar 4a
3.5 Svar 4a
Svar 4b
3.5 Svar 4b
Lösning 4b
3.5 Lösning 4b
Svar 4c
3.5 Svar 4c
Lösning 4c
3.5 Lösning 4c
Svar 4d
3.5 Svar 4d
Lösning 4d
3.5 Lösning 4d


Övning 5

En fårherde vill samla sina får vid en mur i ett rektangulärt stängsel.

Hon/han avgränsar stängslet med ett rep och pinnar i marken enligt

figuren. Repet är \( \, 9 \; {\rm m} \, \) långt (rött).

Beteckna rektangelns kortare sida med \( \, x \). Hur ska fårherden välja

stängslets mått för att få den störst möjliga arean \( \, A \, \) för sina får?


a)   Skriv \( \, A \, \) som en funktion av \( \, x \), problemets målfunktion \( \, A(x) \, \).

b)   Ange målfunktionens definitionsmängd.

c)   Bestäm \( \, x \, \) så att stängslets area blir maximal.

d)   Beräkna stängslets maximala area.

e)   Har problemet ett bivillkor? Om ja, ange det.

    Ovn 355 80.jpg
Svar 5a
3.5 Svar 5a
Lösning 5a
3.5 Lösning 5a
Svar 5b
3.5 Svar 5b
Svar 5c
3.5 Svar 5c
Lösning 5c
3.5 Lösning 5c
Svar 5d
3.5 Svar 5d
Lösning 5d
3.5 Lösning 5d
Svar 5e
3.5 Svar 5e
Lösning 5e
3.5 Lösning 5e



C-övningar: 6-7


Övning 6

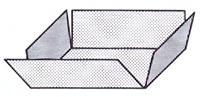
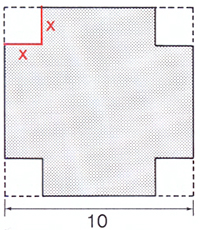
Du ska bygga en öppen låda av en kvadratisk kartong på \( \, 10 \times 10 \; {\rm dm} \, \).

Det gör du genom att skära ut små kvadrater av längden \( \, x \, \) från karton-

gens fyra hörn enligt figuren.

Hur ska du välja \( \, x \, \) för att få den största möjliga volymen \( \, V \, \) för din

öppna låda?

a)   Inför en ny beteckning och ange problemets bivillkor, se Lösning 5 e).

b)   Ställ upp problemets målfunktion \( \, V(x) \, \).

c)   Ange målfunktionens definitionsmängd.

d)   Bestäm \( \, x \, \) så att lådans volym \( \, V(x) \, \) blir maximal.

e)   Beräkna lådans maximala volym.

f)   Vilka mått har lådan med maximal volym?

Ange dina svar med två decimaler.

       Ovn 356 Oppen lada 1 80.jpg

       Ovn 356 Oppen lada 2 80.jpg

Svar 6a
3.5 Svar 6a
Lösning 6a
3.5 Lösning 6a
Svar 6b
3.5 Svar 6b
Lösning 6b
3.5 Lösning 6b
Svar 6c
3.5 Svar 6c
Lösning 6c
3.5 Lösning 6c
Svar 6d
3.5 Svar 6d
Lösning 6d
3.5 Lösning 6d
Svar 6e
3.5 Svar 6e
Lösning 6e
3.5 Lösning 6e
Svar 6f
3.5 Svar 6f
Lösning 6f
3.5 Lösning 6f


Övning 7

SJ har \( \, 20\,000 \, \) passagerare per månad på en viss bansträcka med ett biljettpris på \( \, 200 \, \) kr.

En marknadsundersökning visar att varje höjning av biljettpriset med \( \, 1 \, \) kr skulle medföra

en förlust av \( \, 80 \, \) passagerare per månad.

Vilken biljettprishöjning kommer att maximera intäkten per månad?

a)   Ange problemets bivillkor om

\( \qquad\;\; x \, = \, \) Den planerade prishöjningen i kr.

\( \qquad\;\; y \, = \, \) Antalet passagerare per månad efter prishöjningen \( \, x \, \).

b)   Ställ upp problemets målfunktion \( \, I(x) \, \) för SJ:s intäkt per månad.

c)   Bestäm \( \, x \, \) så att intäkten \( \, I(x) \, \) blir så stor som möjligt.

d)   Beräkna den maximala intäkten efter en biljettprishöjning på \( \, x \, \) kr.

e)   För vilka prishöjningar kommer det inte längre att löna sig att höja biljettpriset?

Svar 7a
3.5 Svar 7a
Lösning 7a
3.5 Lösning 7a
Svar 7b
3.5 Svar 7b
Lösning 7b
3.5 Lösning 7b
Svar 7c
3.5 Svar 7c
Lösning 7c
3.5 Lösning 7c
Svar 7d
3.5 Svar 7d
Lösning 7d
3.5 Lösning 7d
Svar 7e
3.5 Svar 7e
Lösning 7e
3.5 Lösning 7e



A-övningar: 8-9


Övning 8

En cylinder är placerad inuti en kon enligt figuren. Kons mått är givna:
\[ R \, = \, {\rm Radien\;till\;kons\;bascirkel\;} \, = \, 15 \; {\rm cm} \]
\[ H \, = \, {\rm Kons\;höjd\;} \, = \, 30 \; {\rm cm} \]

Vilka mått på cylindern maximerar dess volym \( \, V \, \)?

a)   Formulera problemets bivillkor. Använd den röda triangeln i figuren.

b)   Ställ upp problemets målfunktion \( \, V(r) \, \) där \( r = \) cylinderns radie.

c)   Bestäm cylinderns radie \( \, r \, \) och höjd \( \, h \, \) så att volymen blir maximal.

d)   Beräkna cylinderns maximala volym.

e)   Vilket förhållande råder mellan cylinderns radie \( \, r \, \) och dess höjd \( \, h \, \)

när volymen maximeras?
        Ovn 358 140.jpg
Svar 8a
3.5 Svar 8a
Lösning 8a
3.5 Lösning 8a
Svar 8b
3.5 Svar 8b
Lösning 8b
3.5 Lösning 8b
Svar 8c
3.5 Svar 8c
Lösning 8c
3.5 Lösning 8c
Svar 8d
3.5 Svar 8d
Lösning 8d
3.5 Lösning 8d
Svar 8e
3.5 Svar 8e
Lösning 8e
3.5 Lösning 8e


Övning 9

För att producera en cylinderformad konservburk har man en viss mängd \( \, A \, \)

plåt till förfogande (efter spill). Dvs cylinderns begränsningsarea \( \, = \, A \; {\rm cm}^2 \, \).

I genomgången, Exempel 3 Konservburk, löstes denna uppgift för \( \, A = 500 \).

Här ska du lösa den generellt för en given konstant \( \, A \, \).

Vilka mått på konserven maximerar volymen?

a)   Formulera problemets bivillkor.

b)   Ställ upp problemets målfunktion.

c)   Bestäm cylinderns radie så att burkens volym blir maximal.

d)   Bestäm cylinderns höjd när burkens volym maximeras och visa:

För en cylinder med maximal volym gäller för radien \( \, r \, \) och höjden \( \, h \, \):
     Konservburk 40a.jpg


\[ 2 \; r \; = \; h \]
Svar 9a
3.5 Svar 9a
Lösning 9a
3.5 Lösning 9a
Svar 9b
3.5 Svar 9b
Lösning 9b
3.5 Lösning 9b
Svar 9c
3.5 Svar 9c
Lösning 9c
3.5 Lösning 9c
Svar 9d
3.5 Svar 9d
Lösning 9d
3.5 Lösning 9d





Copyright © 2011-2016 Math Online Sweden AB. All Rights Reserved.

Hämtad från "https://matte3c.mathonline.se/index.php?title=3.5_Övningar_till_Extremvärdesproblem&oldid=36253"