Skillnad mellan versioner av "1.3 Fördjupning till Rationella uttryck"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (140 mellanliggande versioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
| + | __NOTOC__ | ||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| − | {{Not selected tab|[[1. | + | {{Not selected tab|[[1.2 Faktorisering av polynom| << Förra avsnitt]]}} |
{{Not selected tab|[[1.3 Rationella uttryck|Genomgång]]}} | {{Not selected tab|[[1.3 Rationella uttryck|Genomgång]]}} | ||
{{Not selected tab|[[1.3 Övningar till Rationella uttryck|Övningar]]}} | {{Not selected tab|[[1.3 Övningar till Rationella uttryck|Övningar]]}} | ||
| Rad 8: | Rad 9: | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| − | [[1. | + | [[1.3 Repetition: Tal i bråkform| << Repetition: Tal i bråkform]] |
| − | + | ||
| − | + | ||
| + | <!-- [[Media: Lektion 6 Rationella uttryck Rutab.pdf|<b><span style="color:blue">Lektion 6 Rationella uttryck</span></b>]] | ||
[[Media: Lektion 7 Rationella uttryck Ruta.pdf|<b><span style="color:blue">Lektion 7 Rationella uttryck</span></b>]] | [[Media: Lektion 7 Rationella uttryck Ruta.pdf|<b><span style="color:blue">Lektion 7 Rationella uttryck</span></b>]] | ||
| − | + | [[Media: Lektion 8 Rationella uttryck Ruta.pdf|<b><span style="color:blue">Lektion 8 Rationella uttryck: Fördjupning</span></b>]] --> | |
| − | [[Media: Lektion 8 Rationella uttryck Ruta.pdf|<b><span style="color:blue">Lektion 8 Rationella uttryck: Fördjupning</span></b>]] | + | |
| − | + | ||
| − | + | ||
<big> | <big> | ||
| − | + | <div class="border-divblue"> | |
| + | <b><span style="color:#931136">Division med <math> \, 0 \, </math> är inom de reella talen inte definierad.</span></b> | ||
| + | </div> | ||
| − | ::: | + | <math> \quad </math> [http://34.248.89.132:1800/index.php?title=Varf%C3%B6r_%C3%A4r_division_med_0_inte_definierad%3F <b><span style="color:blue">Varför?</span></b>] |
| + | <math> \qquad\qquad\qquad </math> [http://34.248.89.132:1800/index.php/Vad_som_kan_hända_om_man_ändå_dividerar_med_0 <b><span style="color:blue">Vad händer om man ändå dividerar med 0?</span></b>] | ||
| + | </big> | ||
| − | |||
| − | <b><span style="color: | + | == <b><span style="color:#931136">Rationella funktioner</span></b> == |
| − | + | <big> | |
| − | + | En <b><span style="color:red">rationell funktion</span></b> är ett rationellt uttryck som tilldelas en annan variabel, t.ex. <math> \, y</math>. | |
| − | + | ||
| − | + | ||
| − | + | ||
</big> | </big> | ||
| − | <div class=" | + | <div class="ovnC"> |
| − | === | + | === <span style="color:#931136">Exempel 1</span> === |
| + | Det rationella uttrycket <math> \, \displaystyle{\frac{1}{x}} \, </math> tilldelas variabeln <math> \, y \, </math>, vilket ger den <b><span style="color:red">rationella funktionen</span></b> samt grafen: | ||
| − | + | <div class="border-div20"> <big><math> \displaystyle y = {1 \over x} </math></big> </div> [[Image: Praktisk forklaring.jpg]] | |
| − | + | :::::::<b><span style="color:red">Funktionen är inte definierad för <math> \; {\color{Red} {x = 0}} </math>. </span></b> | |
| − | : | + | Till skillnad från polynomfunktioners graf har denna graf två skilda grenar, uttryckt i matematiska termer: |
| − | + | En polynomfunktion är alltid kontinuerlig: Dess graf kan ritas utan att man lyfter pennan från papperet. | |
| − | + | I grafen ovan måste vid <math> x = 0\, </math> pennan lyftas för att gå från grafens ena gren till den andra. | |
| − | + | Dvs grafen är inte sammanhängande i <math> x = 0\, </math>. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Man säger att funktionen är <b><span style="color:red">diskontinuerlig</span></b> (icke-kontinuerlig) i <math> \, x = 0 </math>. | |
| − | + | Anledningen till denna <b><span style="color:red">diskontinuitet</span></b> är att <math> \; y = </math> <math> \displaystyle {1 \over x} \; </math> inte är definierad för <math> x = 0\, </math>. | |
| − | <math> \ | + | När <math> \, x \, </math> närmar sig <math> 0\, </math> går <math> y\, </math> mot oändligheten, vilket kan inses både algebraiskt och grafiskt. |
| − | + | Man måste undanta <math> x = 0\, </math> från funktionens definitionsmängd: | |
| − | < | + | Den rationella funktionen <math> y = </math> <math> \displaystyle {1 \over x}</math><span style="color:black">:s</span> <b><span style="color:red">definitionsmängd</span></b> är<span style="color:black">:</span> <math> \qquad \boxed{{\rm Alla}\quad x \quad {\rm med} \quad x \neq 0} </math> |
| − | + | ||
| − | <span style="color: | + | |
</div> | </div> | ||
| + | <big>Matte 2: | ||
| − | + | <div class="border-divblue"> | |
| − | <div class=" | + | En funktions <b><span style="color:red">definitionsmängd</span></b> är mängden av alla <math> \, x \, </math> för vilka funktionen är definierad. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</div> | </div> | ||
| − | |||
| − | < | + | Diskontinuiteten <u>för vissa</u> <math> \, x \, </math> är något typiskt för alla rationella funktioner och |
| − | + | ||
| − | + | det är det som skiljer dem från polynomfunktioner som är definierade och kontinuerliga för <u>alla</u> <math> x\, </math>. | |
| − | + | Diskontinuiteten <u>för vissa</u> <math> \, x\, </math> innebär att det är bara några isolerade <math> \, x</math>-värden som en rationell funktion <u>kan</u> vara diskontinuerlig för. | |
| − | </ | + | |
| − | + | Det finns även rationella funktioner som inte har några reella diskontinuiteter, dvs de är kontinuerliga för alla reella <math> \, x\, </math>. Här följer ett exempel: | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</big> | </big> | ||
| − | == | + | <div class="ovnC"> |
| + | === <span style="color:#931136">Exempel 2</span> === | ||
| + | En "snäll" rationell funktion samt graf utan reell diskontinuitet: | ||
| + | <div class="border-div20"> <big><math> \displaystyle y_1 = {6\,x \over x^2 + 1} </math></big> </div> [[Image: Rat_fkt_utan_disk.jpg]] | ||
| − | |||
| − | |||
| − | + | <b><span style="color:red">Grafen</span></b> visar inga diskontinuiteter. | |
| − | + | ||
| + | <b><span style="color:red">Algebraiskt</span></b> har funktionsuttryckets nämnare inga reella nollställen, dvs ekvationen | ||
| − | < | + | <math> x^2 + 1 = 0\, </math> saknar reell lösning. Den ger nämligen <math> \, x^2 = -1 </math>. Och <math> \, \sqrt{-1} \, </math> är inget reellt tal. |
| − | + | ||
| − | + | Ekvationen har endast de komplexa lösningarna <math> \, x_1 = i \, </math> och <math> \, x_2 = -i </math>. | |
| − | + | ||
| − | + | <b>Slutsats:</b> Den rationella funktionen <math> \, y_1</math><span style="color:black">:s</span> <b><span style="color:red">definitionsmängd</span></b> är<span style="color:black">:</span> <math> \quad\;\; \boxed{{\rm Alla\;reella\;tal}\quad x} </math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | Den | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</div> | </div> | ||
| − | + | <div class="ovnA"> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <div class=" | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
=== <span style="color:#931136">Exempel 3</span> === | === <span style="color:#931136">Exempel 3</span> === | ||
| − | + | En liten ändring i <math> \, y_1</math>:s nämnare från <math> \, x^2 \, \bf{{\color{Red} +}} \, 1 \, </math> till <math> \, x^2 \, \bf{{\color{Red} -}} \, 1 \, </math> resulterar i en annan funktion med ett annat beteende: | |
| − | + | ||
| − | En liten ändring i <math> \, y_1</math>:s nämnare från <math> \, x^2 \, \bf{{\color{Red} +}} \, 1 \, </math> till <math> \, x^2 \, \bf{{\color{Red} -}} \, 1 \, </math> resulterar i en annan funktion med ett | + | |
| − | <div class="border- | + | <div class="border-div20"> <big><math> \displaystyle y_2 = {6\,x \over x^2 - 1} = {6\,x \over (x + 1) \cdot (x - 1)} </math></big> </div> [[Image: Rat_fkt_med_disk.jpg]] |
| − | <b><span style="color:red">Grafen</span></b> är updelad i tre grenar och har två diskontinuiteter, dvs ställen där den inte är | + | <b><span style="color:red">Grafen</span></b> är updelad i tre grenar och har två diskontinuiteter, dvs två ställen där den inte är kontinuerlig, |
| − | När <math> \, x\, </math> närmar sig dessa två ställen går <math> \, y_2\,</math> mot oändligheten. | + | dvs inte sammanhängande<span style="color:black">:</span> <math> \, x\, = \, -1 \, </math> och <math> \, x\, = \, 1 </math>. När <math> \, x\, </math> närmar sig dessa två ställen går <math> \, y_2\,</math> mot oändligheten. |
<b><span style="color:red">Algebraiskt</span></b> har nämnaren i <math> \, y_2 \, </math> nollställena <math> \, x = 1 \, </math> och <math> \, x = -1 </math>. Därför har <math> \, y_2 \, </math> diskontinuiteter i dessa punkter. | <b><span style="color:red">Algebraiskt</span></b> har nämnaren i <math> \, y_2 \, </math> nollställena <math> \, x = 1 \, </math> och <math> \, x = -1 </math>. Därför har <math> \, y_2 \, </math> diskontinuiteter i dessa punkter. | ||
| Rad 219: | Rad 109: | ||
:::::::::::::<big><math> \Downarrow </math></big> | :::::::::::::<big><math> \Downarrow </math></big> | ||
| − | <b>Slutsats:</b> Den rationella funktionen <math> \, y_2 | + | <b>Slutsats:</b> Den rationella funktionen <math> \, y_2</math><span style="color:black">:s</span> <b><span style="color:red">definitionsmängd</span></b> är<span style="color:black">:</span> <math> \qquad \boxed{{\rm Alla}\quad x \quad {\rm med} \quad x \neq -1 \; {\rm och} \; x \neq 1} </math> |
| − | + | </div> | |
| − | + | ||
| − | + | ||
<div class="ovnC"> | <div class="ovnC"> | ||
| − | === <b><span style="color:#931136"> | + | === <b><span style="color:#931136">Hävbara och icke-hävbara diskontinuiteter</span></b> === |
<div class="exempel"> | <div class="exempel"> | ||
| Rad 235: | Rad 123: | ||
</div> | </div> | ||
| − | Vi skriver de rationella uttrycken ovan som funktioner för att besvara | + | Vi skriver de rationella uttrycken ovan som funktioner och ritar deras grafer för att besvara |
| + | <b>Frågan:</b> Är det <b>en</b> funktion i två olika skepnader eller är det <b>två</b> olika funktioner? | ||
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td><div class="border- | + | <td><div class="border-div20"> |
| − | + | <math>\begin{align} f\,(x) & = {2\,x^2 + 6\,x \over x^2 - 9} = {2\,x\,{\color{Red} {(x + 3)}} \over {\color{Red} {(x + 3)}}\,(x - 3)} \\ | |
| − | + | g\,(x) & = {2\,x \over x - 3} | |
| − | + | \end{align} </math> | |
| + | </div> | ||
| + | <b>Svaret:</b> <math> f(x) \, </math> och <math> \, g\,(x) \, </math> är <b><span style="color:red">två olika funktioner</span></b> eftersom | ||
| + | |||
| + | deras definitionsmängder är olika<span style="color:black">:</span> | ||
| + | |||
| + | <math> f(x)</math><span style="color:black">:s</span> <b><span style="color:red">definitionsmängd</span></b> är<span style="color:black">:</span> <math> \boxed{{\rm Alla} \, x \, {\rm med} \, x \neq -3 \, {\rm och} \, x \neq 3} </math> | ||
| + | |||
| + | <math> g\,(x)</math><span style="color:black">:s</span> <b><span style="color:red">definitionsmängd</span></b> är<span style="color:black">:</span> <math> \boxed{{\rm Alla} \, x \, {\rm med} \, x \neq 3} </math> | ||
| + | </td> | ||
<td>[[Image: Havbar_ickehavbar_disk.jpg]]</td> | <td>[[Image: Havbar_ickehavbar_disk.jpg]]</td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
| − | |||
| − | |||
| − | |||
| − | |||
<b><span style="color:red">OBS!</span></b> Likheten <math> \, {2\,x\,{\color{Red} {(x + 3)}} \over {\color{Red} {(x + 3)}}\,(x - 3)} \, = \, {2\,x \over x - 3} \, </math> gäller inte för alla <math> \, x \, </math> utan endast för alla <math> \, x \not= -3 </math>. Anledningen är: | <b><span style="color:red">OBS!</span></b> Likheten <math> \, {2\,x\,{\color{Red} {(x + 3)}} \over {\color{Red} {(x + 3)}}\,(x - 3)} \, = \, {2\,x \over x - 3} \, </math> gäller inte för alla <math> \, x \, </math> utan endast för alla <math> \, x \not= -3 </math>. Anledningen är: | ||
| Rad 255: | Rad 149: | ||
:::Förkortningen med <math> \, {\color{Red} {(x + 3)}} \, </math> är endast korrekt om <math> \, x \not= -3 </math> eftersom den innebär division med <math> \, {\color{Red} {(x + 3)}} \, </math> som är <math> \, 0\,</math> när <math> \, x = -3\, </math>. | :::Förkortningen med <math> \, {\color{Red} {(x + 3)}} \, </math> är endast korrekt om <math> \, x \not= -3 </math> eftersom den innebär division med <math> \, {\color{Red} {(x + 3)}} \, </math> som är <math> \, 0\,</math> när <math> \, x = -3\, </math>. | ||
| − | :::Se upp för division med <math> \, 0 \,</math> i uttryck, för den är oftast gömd. Läs: [http:// | + | :::Se upp för division med <math> \, 0 \,</math> i uttryck, för den är oftast gömd. Läs: [http://34.248.89.132:1800/index.php/Vad_som_kan_hända_om_man_ändå_dividerar_med_0 <b><span style="color:blue">Vad händer om man ändå dividerar med 0 ?</span></b>]. |
Graferna lurar oss: Med blotta ögat ser man knappast någon skillnad mellan <math> f(x) \, </math> och <math> \, g\,(x) </math>. Men om du förstorar <math> f(x)</math>:s graf kan du se i den ett "hål" eller en "lucka" i <math> \, x = -3 </math>, vilket beror på att <math> f(x) \, </math> inte är definierad där. Grafen "hoppar" över <math> \, x = -3 \, </math> så att säga. Men till skillnad från <math> \, x = 3 \, </math> går funktionen inte mot oändligheten i den närmaste omgivningen av <math> \, x = -3 </math>. Anledningen till det är att <math> \, x = -3 \, </math> är en <b><span style="color:red">hävbar diskontinuitet</span></b>, till skillnad från <math> \, x = 3 \, </math> som är en <b><span style="color:red">icke-hävbar diskontinuitet</span></b>. | Graferna lurar oss: Med blotta ögat ser man knappast någon skillnad mellan <math> f(x) \, </math> och <math> \, g\,(x) </math>. Men om du förstorar <math> f(x)</math>:s graf kan du se i den ett "hål" eller en "lucka" i <math> \, x = -3 </math>, vilket beror på att <math> f(x) \, </math> inte är definierad där. Grafen "hoppar" över <math> \, x = -3 \, </math> så att säga. Men till skillnad från <math> \, x = 3 \, </math> går funktionen inte mot oändligheten i den närmaste omgivningen av <math> \, x = -3 </math>. Anledningen till det är att <math> \, x = -3 \, </math> är en <b><span style="color:red">hävbar diskontinuitet</span></b>, till skillnad från <math> \, x = 3 \, </math> som är en <b><span style="color:red">icke-hävbar diskontinuitet</span></b>. | ||
| Rad 317: | Rad 211: | ||
| − | [[Matte:Copyrights|Copyright]] © | + | [[Matte:Copyrights|Copyright]] © 2019 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved. |
Nuvarande version från 2 juni 2019 kl. 11.48
| << Förra avsnitt | Genomgång | Övningar | Fördjupning | Nästa avsnitt >> |
Division med \( \, 0 \, \) är inom de reella talen inte definierad.
\( \quad \) Varför? \( \qquad\qquad\qquad \) Vad händer om man ändå dividerar med 0?
Rationella funktioner
En rationell funktion är ett rationellt uttryck som tilldelas en annan variabel, t.ex. \( \, y\).
Exempel 1
Det rationella uttrycket \( \, \displaystyle{\frac{1}{x}} \, \) tilldelas variabeln \( \, y \, \), vilket ger den rationella funktionen samt grafen:
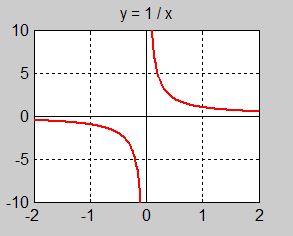
- Funktionen är inte definierad för \( \; {\color{Red} {x = 0}} \).
Till skillnad från polynomfunktioners graf har denna graf två skilda grenar, uttryckt i matematiska termer:
En polynomfunktion är alltid kontinuerlig: Dess graf kan ritas utan att man lyfter pennan från papperet.
I grafen ovan måste vid \( x = 0\, \) pennan lyftas för att gå från grafens ena gren till den andra.
Dvs grafen är inte sammanhängande i \( x = 0\, \).
Man säger att funktionen är diskontinuerlig (icke-kontinuerlig) i \( \, x = 0 \).
Anledningen till denna diskontinuitet är att \( \; y = \) \( \displaystyle {1 \over x} \; \) inte är definierad för \( x = 0\, \).
När \( \, x \, \) närmar sig \( 0\, \) går \( y\, \) mot oändligheten, vilket kan inses både algebraiskt och grafiskt.
Man måste undanta \( x = 0\, \) från funktionens definitionsmängd:
Den rationella funktionen \( y = \) \( \displaystyle {1 \over x}\):s definitionsmängd är: \( \qquad \boxed{{\rm Alla}\quad x \quad {\rm med} \quad x \neq 0} \)
Matte 2:
En funktions definitionsmängd är mängden av alla \( \, x \, \) för vilka funktionen är definierad.
Diskontinuiteten för vissa \( \, x \, \) är något typiskt för alla rationella funktioner och
det är det som skiljer dem från polynomfunktioner som är definierade och kontinuerliga för alla \( x\, \).
Diskontinuiteten för vissa \( \, x\, \) innebär att det är bara några isolerade \( \, x\)-värden som en rationell funktion kan vara diskontinuerlig för.
Det finns även rationella funktioner som inte har några reella diskontinuiteter, dvs de är kontinuerliga för alla reella \( \, x\, \). Här följer ett exempel:
Exempel 2
En "snäll" rationell funktion samt graf utan reell diskontinuitet:
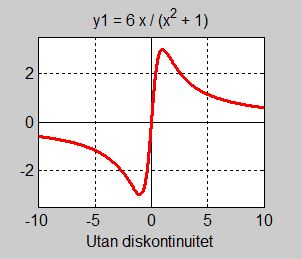
Grafen visar inga diskontinuiteter.
Algebraiskt har funktionsuttryckets nämnare inga reella nollställen, dvs ekvationen
\( x^2 + 1 = 0\, \) saknar reell lösning. Den ger nämligen \( \, x^2 = -1 \). Och \( \, \sqrt{-1} \, \) är inget reellt tal.
Ekvationen har endast de komplexa lösningarna \( \, x_1 = i \, \) och \( \, x_2 = -i \).
Slutsats: Den rationella funktionen \( \, y_1\):s definitionsmängd är: \( \quad\;\; \boxed{{\rm Alla\;reella\;tal}\quad x} \)
Exempel 3
En liten ändring i \( \, y_1\):s nämnare från \( \, x^2 \, \bf{{\color{Red} +}} \, 1 \, \) till \( \, x^2 \, \bf{{\color{Red} -}} \, 1 \, \) resulterar i en annan funktion med ett annat beteende:
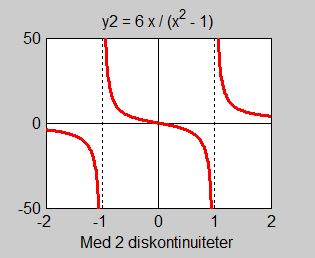
Grafen är updelad i tre grenar och har två diskontinuiteter, dvs två ställen där den inte är kontinuerlig,
dvs inte sammanhängande: \( \, x\, = \, -1 \, \) och \( \, x\, = \, 1 \). När \( \, x\, \) närmar sig dessa två ställen går \( \, y_2\,\) mot oändligheten.
Algebraiskt har nämnaren i \( \, y_2 \, \) nollställena \( \, x = 1 \, \) och \( \, x = -1 \). Därför har \( \, y_2 \, \) diskontinuiteter i dessa punkter.
- \( \Downarrow \)
Slutsats: Den rationella funktionen \( \, y_2\):s definitionsmängd är: \( \qquad \boxed{{\rm Alla}\quad x \quad {\rm med} \quad x \neq -1 \; {\rm och} \; x \neq 1} \)
Hävbara och icke-hävbara diskontinuiteter
Vi skriver de rationella uttrycken ovan som funktioner och ritar deras grafer för att besvara
Frågan: Är det en funktion i två olika skepnader eller är det två olika funktioner?
OBS! Likheten \( \, {2\,x\,{\color{Red} {(x + 3)}} \over {\color{Red} {(x + 3)}}\,(x - 3)} \, = \, {2\,x \over x - 3} \, \) gäller inte för alla \( \, x \, \) utan endast för alla \( \, x \not= -3 \). Anledningen är:
- Förkortningen med \( \, {\color{Red} {(x + 3)}} \, \) är endast korrekt om \( \, x \not= -3 \) eftersom den innebär division med \( \, {\color{Red} {(x + 3)}} \, \) som är \( \, 0\,\) när \( \, x = -3\, \).
- Se upp för division med \( \, 0 \,\) i uttryck, för den är oftast gömd. Läs: Vad händer om man ändå dividerar med 0 ?.
Graferna lurar oss: Med blotta ögat ser man knappast någon skillnad mellan \( f(x) \, \) och \( \, g\,(x) \). Men om du förstorar \( f(x)\):s graf kan du se i den ett "hål" eller en "lucka" i \( \, x = -3 \), vilket beror på att \( f(x) \, \) inte är definierad där. Grafen "hoppar" över \( \, x = -3 \, \) så att säga. Men till skillnad från \( \, x = 3 \, \) går funktionen inte mot oändligheten i den närmaste omgivningen av \( \, x = -3 \). Anledningen till det är att \( \, x = -3 \, \) är en hävbar diskontinuitet, till skillnad från \( \, x = 3 \, \) som är en icke-hävbar diskontinuitet.
\( x = -3 \) kallas för en hävbar diskontinuitet eftersom \( (x+3) \) kan förkortas bort i \( f(x) \) och försvinner då från nämnaren.
\( \, x = 3 \, \) kallas för en icke-hävbar diskontinuitet eftersom \( \, (x-3) \, \) finns kvar i nämnaren av \( f(x) \).
Men hur häver man en hävbar diskontinuitet?
Kontinuerlig fortsättning
Hävbara diskontinuiteter är "snälla". Funktioner med hävbara diskontinuiteter kan "repareras":
Det gör man genom att definiera en ny funktion som inte längre har den ursprungliga funktionens hävbara diskontinuitet, men är annars identisk med den.
I exemplet ovan skulle man kunna t.ex. komplettera funktionen \( f(x)\, \):s definition med ett värde för \( \, x = -3 \, \) som gör att den nya funktionen blir kontinuerlig i sin omgivning. Man får fram detta värde genom att beräkna värdet av \( \, \displaystyle {g\,(x) = {2\,x \over x - 3}} \, \) för \( \, x = -3 \):
- \[ g\,(-3) = {2 \cdot (-3) \over -3 - 3} = {-6 \over -6} = 1 \]
Värdet \( \, 1 \, \) läggs till i den nya funktionen för \( \, x = -3 \). Så blir den kontinuerliga fortsättningen en modifierad version av \( f(x) \) som består just av det här tillägget. För alla andra \( \, x \, \) är den nya funktionen identisk med den gamla \( f(x) \).
Så här kan den nya funktionen \(-\) kallad den kontinuerliga fortsättningen av \( f(x) \) \(-\) definieras:
- \( \hat{f}(x) \, = \, \begin{cases} \displaystyle {2\,x^2 + 6\,x \over x^2 - 9} & \mbox{om } x \neq -3 \\ \\ 1 & \mbox{om } x = -3 \end{cases}\)
Denna definition är uppdelad i två olika fall: För alla \( \, x \neq -3\, \) definieras \( \, \hat{f}(x) \, \) enligt det rationella uttrycket för \( \, f(x)\, \).
- För \( \, x = -3 \, \) får \( \hat{f}(x) \, \) värdet \( 1 \), dvs \( \hat{f}(-3) = 1 \).
\(\hat{f}(x) \, \) är både algebraiskt och grafiskt (se exemplet ovan) identisk med den förkortade form vi hade fått tidigare:
- \[ \hat{f}(x) \, = \, g\,(x) \, = \, {2 \, x \over x - 3} \]
I praktiskt beräkningssammanhang, t.ex. när man ritar grafen, föredrar man förstås denna enkla form.
Nackdelen med den är bara att den inte längre innehåller något spår av den ursprungliga funktionen \( f(x)\, \), att den "gömmer" sina rötter. Man ser inte att den är en kontinuerlig fortsättning av \( f(x) \).
Den andra faktorn \( (x-3)\, \) både i \( f(x)\):s och \( \, \hat{f}(x)\):s nämnare som inte kan förkortas ger upphov till den andra diskontinuiteten \( \, x = 3 \, \) som till skillnad från \( \, x = -3\, \) är en icke-hävbar diskontinuitet och inte kan "repareras" på något sätt. När \( \, x\, \) går mot \( \, 3\, \) går \( f(x)\, \) inte mot ett ändligt värde utan mot oändligheten, vilket syns i graferna till både \( f(x)\, \) och \( \hat{f}(x) \). Denna "allvarliga" diskontinuitet finns även kvar i den kontinuerliga fortsättningen \( \hat{f}(x) \).
Så \( \hat{f}(x) \, \) har endast en diskontinuitet kvar medan \( f(x)\, \) hade två diskontinuiteter.
Copyright © 2019 TechPages AB. All Rights Reserved.