Skillnad mellan versioner av "Huvudsida"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (131 mellanliggande versioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
| − | |||
__NOTOC__ | __NOTOC__ | ||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| − | {{ | + | {{Not selected tab|[[Matte 3c Innehållsförteckning|Innehållsförteckning]]}} |
| − | {{Not selected tab|[[Matte | + | <!-- {{Not selected tab|[[Matte 3c Planering|Planering Matte 3c]]}} --> |
| − | {{Not selected tab|[[Media: | + | {{Not selected tab|[[Media: Centralt_innehall_Ma3c.pdf|Centralt innehåll]]}} |
| − | {{Not selected tab|[[Media: | + | {{Not selected tab|[[Media: Kunskapskrav_Ma3c.pdf|Kunskapskrav]]}} |
| − | {{Not selected tab|[[Media: | + | {{Not selected tab|[[Media: Formelsamling NP Ma3.pdf|Formelsamling Matte 3]]}} |
| + | {{Not selected tab|[[1.3 Rationella uttryck|<b><span style="color:red">Aktuell lektion</span></b>]]}} | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| − | == <big><b> | + | <big><big><big>Välkommen till Matte 3c i [http://www.mathonline.se <b><span style="color:blue">Math Online</span></b>] <math>-</math> ett webbaserat digitalt läromedel för matematik</big></big></big> |
| + | <table> | ||
| + | <tr> | ||
| + | <td> [[Image: Bild_till_vad_ar_mathonline_a.jpg]] | ||
| + | </td> | ||
| + | <td><math> \qquad\quad </math></td> | ||
| + | <td> | ||
| + | |||
| + | |||
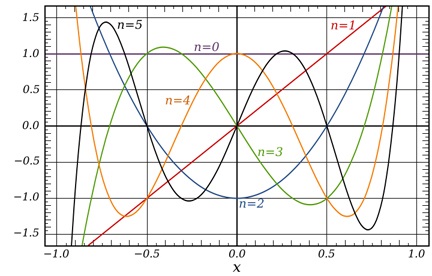
| + | [[Image: Chebyshev_Polyn_2nd_60a.jpg]] | ||
| + | |||
| + | ::<big><big> [[1.1_Fördjupning_till_Polynom#En_familj_av_h.C3.B6gre_grads_polynomfunktioner|Polynomfunktioner av grad <math> \, n = 0, 1, \ldots , 5</math>]]</big></big> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | |||
| + | <div class="ovnE"> | ||
| + | <b>Matematik 3c </b> är en fortsättningskurs och förutsätter förkunskaper från kurser motsvarande Matematik 1c och 2c. | ||
| + | |||
| + | Det som står i fokus av denna kurs är begreppet derivata. För att förbereda eleven på begreppet derivata gås igenom en hel del algebra. | ||
| + | |||
| + | Även olika typer av funktioner som introducerades i kursen Matematik 2c, vidareutvecklas och fördjupas, inkl. naturliga logaritmer. | ||
| + | |||
| + | I kapitlet Användning av derivata lär vi oss att lösa praktiska problem med hjälp av derivata, speciellt extremvärdesproblem. | ||
| + | |||
| + | Kursen fortsätter med derivatans omvända operation, nämligen integration. Det avslutande kapitlet handlar om trigonometri – | ||
| + | |||
| + | läran om beräkning av trianglar. För detaljerat upplägg se [[Matte 3c Innehållsförteckning|<b><span style="color:blue">innehållsförteckningen</span></b>]]. | ||
| + | |||
| + | Matematik 3c är obligatorisk för gymnasiets Naturvetenskapsprogram (NA) och Teknikprogram (TE) och kan ge meritpoäng även som | ||
| + | |||
| + | frivillig kurs för gymnasiets andra program. Den passar också för vuxenutbildningen. | ||
| + | |||
| + | Kursen följer [http://www.skolverket.se/laroplaner-amnen-och-kurser/gymnasieutbildning/gymnasieskola/mat?tos=gy&subjectCode=mat&lang=sv <b><span style="color:blue">Skolverkets ämnesplan GY 2011</span></b>]. | ||
| + | |||
| + | Matematik 3c motsvarar i stora delar den kurs som i den gamla kursplanen hette Matematik C. | ||
| + | </div> | ||
| + | |||
| − | == | + | == Att komma igång med Matte 3c-kursen == |
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td><big>< | + | <td><big> |
| + | * Ovan på sidan hittar du flikar till kursens [[Matte 3c Planering|<b><span style="color:blue">planering</span></b>]] och [[Matte 3c Innehållsförteckning|<b><span style="color:blue">innehålls-</span></b>]]<br> [[Matte 3c Innehållsförteckning|<b><span style="color:blue">förteckning</span></b>]] som följer Skolverkets [[Media: Centralt_innehall_Ma3c.pdf|<b><span style="color:blue">centrala innehåll</span></b>]] (kursplan). | ||
| − | + | * I vänsterspalten ser du länkar till kursens innehåll som du kan an-<br> vända för att navigera genom materialet. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | * Kursen är indelad i fem kapitel. Varje kapitel innehåller ett antal av-<br> snitt och avslutas med diagnosprov samt fullständiga lösningar. | ||
| − | < | + | * Varje avsnitt börjar med en [[1.1 Polynom|<b><span style="color:blue">genomgång</span></b>]] som behandlar grundbe-<br> grepp med hjälp av enkla lösta exempel och förklaringar. |
| − | + | * Vissa avsnitt har repeterande, fördjupande eller tillämpande under-<br> avsnitt. T.ex. är [[Potenser|<b><span style="color:blue">Potenser</span></b>]] ett repeterande underavsnitt i avsnittet<br> [[1.1 Polynom|<b><span style="color:blue">Polynom</span></b>]]. | |
| − | + | ||
| − | + | ||
| − | : | + | |
| − | + | ||
| − | < | + | |
| + | * Till varje avsnitt finns det [[1.1 Övningar till Polynom|<strong><span style="color:blue">övningar</span></strong>]] indelad i tre kategorier: E-, C-<br> och A-nivå samt svar (facit) och fullständiga lösningar. Ex.<span style="color:black">:</span> <math> \to </math> | ||
| − | < | + | * När man är klar med ett kapitel är det dags för [[Diagnosprov 1 i Matte 3 kap 1 Algebra och funktioner|<b><span style="color:blue">diagnosprov</span></b>]] som<br> ska förbereda på det riktiga provet. |
| − | + | * Till varje diagnosprov finns [[Lösningar till diagnosprov 1 i Matte 3 kap 1 Algebra och funktioner|<b><span style="color:blue">fullständiga lösningar</span></b>]] som man kan<br> använda för att själv (eller låta en kompis) rätta sitt diagnosprov. | |
| − | : | + | </big> |
| − | + | </td> | |
| − | + | <td> </td> | |
| − | + | <td><math> \quad </math> <big><span style="color:blue">>></span> <math> \quad </math> <div class="ovnE">{{#NAVCONTENT:Exempel på en övning|1.2 Övning 3a}}</div></big> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | < | + | |
| − | < | + | |
| − | < | + | <math> \quad </math> <big><span style="color:blue">>></span> <math> \quad </math> <div class="ovnC">{{#NAVCONTENT:Exempel på övningens svar|1.2 Svar 3a}}</div></big> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <math> \quad </math> <big><span style="color:blue">>></span> <math> \quad </math> <div class="ovnA">{{#NAVCONTENT:Exempel på övningens fullständiga lösning|1.2 Lösning 3a}}</div></big> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <big> | ||
| + | * Diagnosprovens resultat kan diskuteras med din lärare för att få både [http://www.jisc.ac.uk/guides/feedback-and-feed-forward <b><span style="color:blue">feedback</span></b>] och [http://www.edweek.org/tsb/articles/2012/03/01/02formative.h05.html <b><span style="color:blue">feed-forward</span></b>] samt kunna vidareutveckla dina mattekunskaper. | ||
| − | < | + | * Inför det nationella provet i Matte 3c kan man förbereda sig genom att träna på [[Gammalt nationellt prov 2 i Matte 3c|<b><span style="color:blue">gamla nationella prov</span></b>]] med fullständiga lösningar och [[Repetitionsuppgifter inför nationella provet i Matte 3c|<b><span style="color:blue">repetitionsuppgifter</span></b>]]. |
| − | + | * Alla avsnitt innehåller [[1.1_Polynom#Internetl.C3.A4nkar|<strong><span style="color:blue">Internetlänkar</span></strong>]] till kompletterande material, ofta små videos på YouTube, demos, animationer, små spel eller extraövningar. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | * Man kan även söka efter ett matematiskt begrepp i sökfältet <b>Sök</b> längst ner i vänsterspalten för att få fram de sidor som innehåller sökordet. | |
| − | + | </big> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | + | <div class="forsmak"> | |
| − | :: | + | == <b><span style="color:#931136">Exempel och försmak på Math Online:s pedagogik</span></b> == |
| − | + | ||
| − | + | ||
| − | < | + | |
| − | < | + | |
| + | <table> | ||
| + | <tr> | ||
| + | <td><big><big>1. Exempelorienterad undervisning:</big></big> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | |||
| + | |||
| + | <big><big>2. [[1.7_Potenser#Varf.C3.B6r_.C3.A4r_.5C.28_.5C.3B_5.5C.2C.5E0_.5C.2C_.3D_.5C.2C_1_.5C.3B_.5C.29.3F|<span style="color:blue">Varför är <math> \; 5\,^0 \, = \, 1 </math>, medan <math> \, 5 \cdot 0 \, = \, 0 \; </math>?</span>]]</big></big> | ||
| + | |||
| + | |||
| + | <big><big>3. [[Varf%C3%B6r_f%C3%A5r_man_inte_dividera_med_0_%3F|<span style="color:blue">Varför får man inte dividera med <math> \, 0 \, </math>?</span>]]</big></big> | ||
| + | |||
| + | |||
| + | <big><big>4. [http://52.210.62.116:1800/index.php/1.2_Räkneordning#Varf.C3.B6r_g.C3.A5r_multiplikation_f.C3.B6re_addition.3F <span style="color:blue">Varför går multiplikation före addition?</span>]</big></big> | ||
| + | |||
| + | |||
| + | <big><big>5. [http://52.210.62.116:1800/index.php/En_matten%C3%B6t <span style="color:blue">En mattenöt: Cirkel eller kvadrat?</span>]</big></big> | ||
| + | |||
| + | </td> | ||
| + | |||
| + | <td> <math> \quad </math> </td> | ||
| + | |||
| + | <td><span style="color:red"><b>Ekvationer:</b></span> <math> \qquad </math> [http://52.210.62.116:1800/index.php/Flaska_med_pant <span style="color:blue">Flaska med pant</span>] <math> \qquad </math> [http://52.210.62.116:1800/index.php/Att_ställa_upp_en_ekvation <span style="color:blue">Att ställa upp en ekvation</span>] <math> \qquad </math> [http://52.210.62.116:1800/index.php/Lösning_till_flaska_med_pant <span style="color:blue">Lösning</span>] <math> \qquad </math> [http://52.210.62.116:1800/index.php/Svar_till_flaska_med_pant <span style="color:blue">Svar</span>] | ||
| + | |||
| + | <span style="color:red"><b>Genomsnittlig förändringshastighet:</b></span> <math> \qquad </math> [http://52.210.62.116:1800/index.php/2.2_Genomsnittlig_f%C3%B6r%C3%A4ndringshastighet#Exempel_1_Marginalskatt <span style="color:blue">Marginalskatt</span>] <math> \qquad </math> [http://52.210.62.116:1800/index.php/2.2_Genomsnittlig_f%C3%B6r%C3%A4ndringshastighet#Exempel_3_Oljetank <span style="color:blue">Oljetank</span>] | ||
| + | |||
| + | <span style="color:red"><b>Derivata:</b></span> <math> \qquad </math> [http://52.210.62.116:1800/index.php/2.1_Introduktion_till_derivata <span style="color:blue">Simhopp från 10 meterstorn (Elevaktivitet)</span>] | ||
| + | |||
| + | <span style="color:red"><b>Extremvärdesproblem:</b></span> <math> \qquad </math> [http://52.210.62.116:1800/index.php/3.5_Extremvärdesproblem#Exempel_1_Rektangel_i_parabel <span style="color:blue">Rektangel i parabel</span>] <math> \qquad </math> [http://52.210.62.116:1800/index.php/3.5_Extremvärdesproblem#Exempel_2_Glasskiva_.28rektangel_i_triangel.29 <span style="color:blue">Glasskiva</span>] <math> \qquad </math> [http://52.210.62.116:1800/index.php/3.5_Extremvärdesproblem#Exempel_3_Konservburk <span style="color:blue">Konservburk</span>] <math> \qquad </math> | ||
| + | |||
| + | <span style="color:red"><b>Diskreta funktioner:</b></span> <math> \qquad </math> [http://52.210.62.116:1800/index.php/1.5_Kontinuerliga_och_diskreta_funktioner#Exempel_3_Fibonaccis_problem <span style="color:blue">Kaniners fortplantning, även kallad Fibonaccis problem (Digital beräkning med Excel)</span>] | ||
| + | |||
| + | <span style="color:red"><b>Absolutbelopp:</b></span> <math> \qquad </math> [http://52.210.62.116:1800/index.php/1.6_Absolutbelopp#N.C3.A5gra_exempel_p.C3.A5_absolutbelopp <span style="color:blue">Några exempel på absolutbelopp</span>] <math> \qquad </math> [http://52.210.62.116:1800/index.php/1.6_Absolutbelopp#Ekvationer_med_absolutbelopp <span style="color:blue">Ekvationer med absolutbelopp</span>] <math> \qquad </math> [http://52.210.62.116:1800/index.php/1.6_Fördjupning_till_Absolutbelopp#Falska_r.C3.B6tter <span style="color:blue">Falska rötter</span>] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | [http://52.210.62.116:1800/index.php/Teoretisk_förklaring <span style="color:blue">Teoretisk förklaring</span>] <math> \qquad\quad\;\; </math> [http://52.210.62.116:1800/index.php/Praktisk_förklaring <span style="color:blue">Praktisk förklaring</span>] <math> \qquad\quad\;\; </math> [http://52.210.62.116:1800/index.php/Vad_som_kan_h%C3%A4nda_om_man_%C3%A4nd%C3%A5_dividerar_med_0 <span style="color:blue">Vad som kan hända om man ändå gör det</span>] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | [http://52.210.62.116:1800/index.php/Formulering_&_ledning_för_mattenöten <span style="color:blue">Formulering & ledning</span>] <math> \qquad </math> [http://52.210.62.116:1800/index.php/Lösning_till_mattenöten <span style="color:blue">Lösning</span>] <math> \qquad </math> [http://52.210.62.116:1800/index.php/Svar_till_mattenöten <span style="color:blue">Svar</span>] | ||
</td> | </td> | ||
| + | |||
</tr> | </tr> | ||
</table> | </table> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| Rad 164: | Rad 169: | ||
| − | [[Matte:Copyrights|Copyright]] © 2011- | + | [[Matte:Copyrights|Copyright]] © 2011-2019 Math Online Sweden AB. All Rights Reserved. |
Nuvarande version från 3 december 2024 kl. 15.23
| Innehållsförteckning | Centralt innehåll | Kunskapskrav | Formelsamling Matte 3 | Aktuell lektion |
Välkommen till Matte 3c i Math Online \(-\) ett webbaserat digitalt läromedel för matematik

|
\( \qquad\quad \) |
Matematik 3c är en fortsättningskurs och förutsätter förkunskaper från kurser motsvarande Matematik 1c och 2c.
Det som står i fokus av denna kurs är begreppet derivata. För att förbereda eleven på begreppet derivata gås igenom en hel del algebra.
Även olika typer av funktioner som introducerades i kursen Matematik 2c, vidareutvecklas och fördjupas, inkl. naturliga logaritmer.
I kapitlet Användning av derivata lär vi oss att lösa praktiska problem med hjälp av derivata, speciellt extremvärdesproblem.
Kursen fortsätter med derivatans omvända operation, nämligen integration. Det avslutande kapitlet handlar om trigonometri –
läran om beräkning av trianglar. För detaljerat upplägg se innehållsförteckningen.
Matematik 3c är obligatorisk för gymnasiets Naturvetenskapsprogram (NA) och Teknikprogram (TE) och kan ge meritpoäng även som
frivillig kurs för gymnasiets andra program. Den passar också för vuxenutbildningen.
Kursen följer Skolverkets ämnesplan GY 2011.
Matematik 3c motsvarar i stora delar den kurs som i den gamla kursplanen hette Matematik C.
Att komma igång med Matte 3c-kursen
|
\( \quad \) >> \( \quad \)
Exempel på en övning
Exempel på övningens svar
Exempel på övningens fullständiga lösning
|
- Diagnosprovens resultat kan diskuteras med din lärare för att få både feedback och feed-forward samt kunna vidareutveckla dina mattekunskaper.
- Inför det nationella provet i Matte 3c kan man förbereda sig genom att träna på gamla nationella prov med fullständiga lösningar och repetitionsuppgifter.
- Alla avsnitt innehåller Internetlänkar till kompletterande material, ofta små videos på YouTube, demos, animationer, små spel eller extraövningar.
- Man kan även söka efter ett matematiskt begrepp i sökfältet Sök längst ner i vänsterspalten för att få fram de sidor som innehåller sökordet.
Exempel och försmak på Math Online:s pedagogik
| 1. Exempelorienterad undervisning:
2. Varför är \( \; 5\,^0 \, = \, 1 \), medan \( \, 5 \cdot 0 \, = \, 0 \; \)?
|
\( \quad \) | Ekvationer: \( \qquad \) Flaska med pant \( \qquad \) Att ställa upp en ekvation \( \qquad \) Lösning \( \qquad \) Svar
Genomsnittlig förändringshastighet: \( \qquad \) Marginalskatt \( \qquad \) Oljetank Derivata: \( \qquad \) Simhopp från 10 meterstorn (Elevaktivitet) Extremvärdesproblem: \( \qquad \) Rektangel i parabel \( \qquad \) Glasskiva \( \qquad \) Konservburk \( \qquad \) Diskreta funktioner: \( \qquad \) Kaniners fortplantning, även kallad Fibonaccis problem (Digital beräkning med Excel) Absolutbelopp: \( \qquad \) Några exempel på absolutbelopp \( \qquad \) Ekvationer med absolutbelopp \( \qquad \) Falska rötter
Teoretisk förklaring \( \qquad\quad\;\; \) Praktisk förklaring \( \qquad\quad\;\; \) Vad som kan hända om man ändå gör det
|
Copyright © 2011-2019 Math Online Sweden AB. All Rights Reserved.
 Hämtar...
Hämtar...