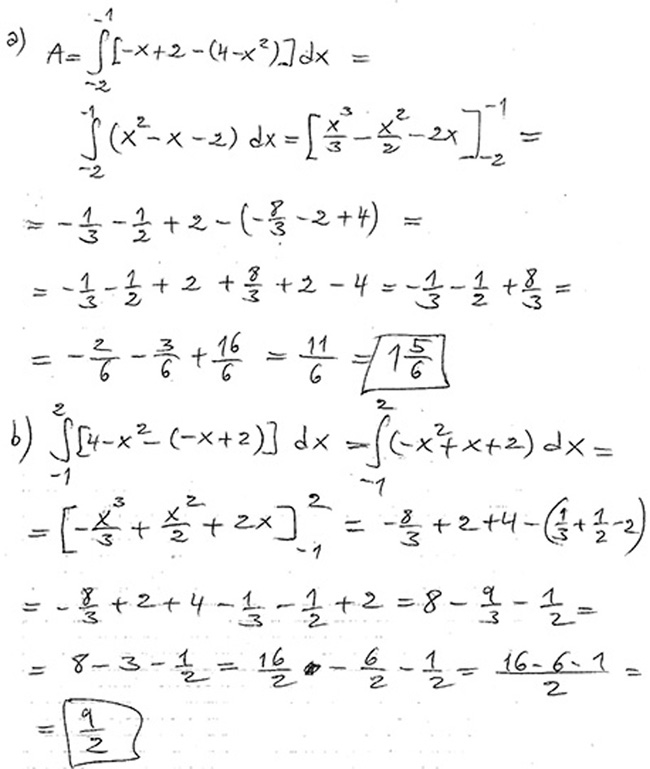Skillnad mellan versioner av "Kapitel 4 Integraler"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 1: | Rad 1: | ||
| + | __NOTOC__ | ||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| − | {{Selected tab|[[ | + | <!-- {{Not selected tab|[[Matte 3 Kapitel 3 Användning av derivata| << Förra kapitel]]}} --> |
| − | {{Not selected tab|[[ | + | {{Selected tab|[[Kapitel 4 Integraler|Genomgångar]]}} |
| + | {{Not selected tab|[[Media: Formelsamling NP Ma3 Integ.pdf|Formelsamling Integraler]]}} | ||
| + | <!-- {{Not selected tab|[[Matte 3c Planering|Planering Matte 3c]]}} | ||
| + | {{Not selected tab|[[Kapitel 5 Trigonometri|Nästa kapitel >> ]]}} --> | ||
| + | {{Not selected tab|[https://matte4.mathonline.se/index.php/Diagnosprov_kap_2/3_Derivator_%26_integraler <b>Diagnos kap 2/3 Der. & int.</b>]}} | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| + | <big> | ||
| + | <br> | ||
| + | F.o.m. detta kapitel finns kursens övningar inte på webben (pga tidsbrist). Därför: Läs igenom genomgångarna här, men använd för | ||
| − | + | övningarna boken (Matematik 5000). Leta i bokens innehållsförteckning och register efter resp. kapitlets/avsnittets övningar. | |
| − | + | ||
| + | Tyvärr överensstämmer sidouppgifterna här inte med boken. | ||
| + | <!-- | ||
| + | == <b><span style="color:#931136">Utdrag ur planeringen:</span></b> == | ||
| + | <br> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 30px;"> [[Image: Planering_Integr_Rubrik_2019_800a.jpg]] </div> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 30px;"> [[Image: Planering_Integraler_2019_800.jpg]] </div> | ||
| − | + | Lektion 29: | |
| + | --> | ||
| + | == <b><span style="color:#931136">4.1 Primitiva funktioner <math> \qquad\qquad\qquad\;\; </math> <small><small>Övningar: Boken, sid 175</small></small></span></b> == | ||
| − | + | <b><span style="color:red">Hittills:</span></b> En funktion var given. Vi sökte funktionens derivata. Nu vänder vi på steken: | |
| + | <b><span style="color:red">Det omvända problemet:</span></b> | ||
| − | <div | + | <div class="border-divblue">Derivatan är given. Sökt är den <b><span style="color:red">ursprungliga</span></b> funktionen till den givna derivatan.</div> |
| + | '''OBS! Annan problemställning och annan beteckning<span style="color:black">:</span>''' | ||
| − | < | + | <math> \; f\,(x) \, </math> är inte längre en given funktion som vi ska derivera. |
| + | <math> \; f\,(x) \, </math> är en given derivata av en okänd funktion <math> \, \color{red} {F\,(x)} \, </math> som vi söker, dvs <math> \, \color{red} {F\,'(x)} = f\,(x) \, </math>. | ||
| − | = | + | <div class="ovnE"> |
| + | <b><span style="color:#931136">Exempel 1:</span></b> | ||
| + | ---- | ||
| + | <u>Givet:</u> <math> \quad\;\; f\,(x) \, = \, 2\,x \, = \, </math> <small> Derivatan av någon funktion </small> | ||
| + | <u>Sökt:</u> <math> \quad\;\;\, F(x) \quad </math> så att <math> \quad F\,'(x) = 2\,x </math> | ||
| − | < | + | <u>Lösning:</u> <math> \;\; F(x) = \boxed{\textstyle x\,^2 \, + C\,} \, , \;\; C={\rm const.} </math> |
| + | <u>Kontroll:</u> <math> \;\; F\,'(x) = 2\,x + 0 \, = \, 2\,x \, = \, f\,(x) </math> | ||
| + | </div> | ||
| − | |||
| + | <div class="border-divblue"><math>F\,(x) = x\,^2 + C \, </math> kallas för <b><span style="color:#931136">primitiv funktion</span></b> till <math> \, f\,(x) = 2\,x </math>. <math> \;\; </math> <b><span style="color:red">Primitiv funktion = "Anti"derivata</span></b>. <math> \;\; </math> | ||
| + | ---- | ||
| + | Att hitta en primitiv funktion kallas för <b><span style="color:#931136">integration</span></b> och <math> \, C \, </math> för <b><span style="color:#931136">integrationskonstanten</span></b>. | ||
| + | </div> | ||
| − | == <b><span style="color:#931136">4.4 | + | |
| + | <table> | ||
| + | <tr> | ||
| + | <td><div class="ovnE"> | ||
| + | <b><span style="color:#931136">Exempel 2:</span></b> | ||
| + | ---- | ||
| + | <u>Givet:</u> <math> \quad\;\; f\,(x) \, = \, x\,^3 + 5 \, = \, </math> <small> Derivatan av någon funktion </small> | ||
| + | |||
| + | <u>Sökt:</u> <math> \quad\;\;\, F(x) \quad </math> så att <math> \quad F\,'(x) = x\,^3 + 5 </math> | ||
| + | |||
| + | <u>Lösning:</u> <math> \;\; F(x) = \boxed{\textstyle \frac{1}{4} x\,^4 + 5 \, x + C\,} \, , \;\; C={\rm const.} </math> | ||
| + | |||
| + | <u>Kontroll:</u> <math> \;\; F\,'(x) = \frac{4}{4} x\,^3 + 5 + 0 \, = \, x\,^3 + 5 \, = \, f\,(x) </math> | ||
| + | </div></td> | ||
| + | <td><math> \quad </math></td> | ||
| + | <td><div class="border-divblue"> | ||
| + | <b><span style="color:#931136">Allmän definition:</span></b> | ||
| + | ---- | ||
| + | <u>Givet:</u> <math> \quad f\,(x) </math> | ||
| + | |||
| + | <u>Sökt:</u> <math> \quad </math> En funktion <math> \;\; F\,(x) \;\; </math> så att<span style="color:black">:</span> | ||
| + | |||
| + | <math> \qquad\qquad\quad\; \boxed{F\,'\,(x) = f\,(x)} </math> | ||
| + | |||
| + | Funktionen <math> \, F\,(x) \, </math> kallas för <b><span style="color:#931136">primitiv funktion</span></b>. | ||
| + | </div></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | |||
| + | :<big> Integration är deriveringens <b><span style="color:red">inversa</span></b> (omvända) operation. Därför:</big> | ||
| + | |||
| + | :<big> Integrationsregler för olika funktionstyper följer genom att vända om deriveringsreglerna. T.ex.:</big> | ||
| + | |||
| + | <table> | ||
| + | <tr> | ||
| + | <td><div class="border-divblue"> | ||
| + | ==== <b><span style="color:#931136">Integrationsregeln för en potens:</span></b> ==== | ||
| + | ---- | ||
| + | Om <math> f(x) = x\,^n \qquad {\rm där} \qquad\, n = {\rm const.} \neq -1</math> | ||
| + | |||
| + | då <math>\; F(x) = \boxed{\frac{x\,^{n+1}}{n+1} \, + \, C\;} \;, C = </math> <b><span style="color:#931136">integrationskonstanten</span></b> | ||
| + | |||
| + | </div></td> | ||
| + | <td><math> \quad </math></td> | ||
| + | <td> | ||
| + | |||
| + | <div class="ovnE"> | ||
| + | <b><span style="color:#931136">Exempel:</span></b> | ||
| + | ---- | ||
| + | För <math> \, f(x) \, = \, x^4 \; </math> blir den primitiva funktionen: | ||
| + | |||
| + | ::<math> \, F(x) \, = \, \frac{x^5}{5} + C \, = \, \frac{1}{5} \, x^5 + C</math> | ||
| + | </div> | ||
| + | |||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | |||
| + | :<big> Bevis<span style="color:black">:</span></big> <math> \, F\,'(x) = \displaystyle \frac{(n+1) \, x\,^{n+1-1}}{n+1} \, + \, 0 \, = \, \frac{(n+1) \, x\,^{n}}{n+1} = x\,^n = f\,(x) \qquad </math> <big> Exempel<span style="color:black">:</span></big> <math> \;\; F\,'(x) \, = \, \displaystyle \frac{5}{5} \, x\,^4 \, + \, 0 \, = \, x\,^4 \, = \, f\,(x) \qquad </math> | ||
| + | |||
| + | :<big> Regeln ovan gäller inte bara för positiva <math> \, n \, </math> utan även för negativa (undantaget <math> -1 </math>) och rationella exponenter.</big> | ||
| + | |||
| + | :<big> Ytterligare regler om primitiva funktioner (för exponentialfunktioner) anges [[Kapitel_4_Integraler#Integrationsregler_f.C3.B6r_exponentialfunktioner:|<b><span style="color:blue">senare</span></b>]].</big> | ||
| + | |||
| + | |||
| + | <big><b>Fysikalisk tolkning:</b></big> | ||
| + | |||
| + | <table> | ||
| + | <tr> | ||
| + | <td><math> \quad </math></td> | ||
| + | <td>[[Image: 0 Hastighetsmatare_60.jpg]]</td> | ||
| + | <td> <big><b> <math> \quad </math> Hastighetsmätaren <span style="color:red">deriverar</span>. <math> \;\; </math> | ||
| + | |||
| + | |||
| + | <math> \quad </math> Trippmätaren <span style="color:red">integrerar</span>, dvs<span style="color:black">:</span> | ||
| + | |||
| + | |||
| + | <math> \quad </math> summerar den körda sträckan. </b></big> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | </td> | ||
| + | <td><math> \quad </math> [[Image: 0 Diff vs Integr_h257.jpg]]</td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | |||
| + | <div class="border-divblue"> | ||
| + | Integration är den <b><span style="color:red">inversa</span></b> operationen till derivering. <math> \quad </math> <b><span style="color:red">Primitiv funktion = "Anti"derivata</span></b> | ||
| + | |||
| + | ::{|class="wikitable" | ||
| + | ! !! Derivata !! Integral | ||
| + | |- | ||
| + | |align="left"| Fysikalisk tolkning: ||align="center"| Hastighet ||align="center"| Sträcka | ||
| + | |- | ||
| + | |align="left"| Geometrisk tolkning: ||align="center"| Kurvans lutning ||align="center"| Area under kurvan | ||
| + | |- | ||
| + | |align="left"| Matematisk tolkning: ||align="center"| Limes av differenskvot ||align="center"| Limes av oändlig summa | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <div class="ovnC"> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 1 Primitiva funktioner_496.jpg]] | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <big>'''Integrationskonstanten <math> \, C \, </math>:'''</big> | ||
| + | |||
| + | <div class="border-divblue"> | ||
| + | Om en given funktion har en primitiva funktion så har den pga <math> \, C={\rm const.} \, </math> oändligt | ||
| + | |||
| + | många primitiva funktioner. | ||
| + | |||
| + | För att få <b><span style="color:red">endast en</span></b> primitiv funktion <math> \, F(x) \, </math> ställs vissa <b><span style="color:red">villkor</span></b> på <math> \, F(x) \, </math>. I fysiken kallas | ||
| + | |||
| + | de för <b><span style="color:red">begynnelsevillkor</span></b>. Villkoren används för att bestämma integrationskonstanten <math> \, C \, </math>. <big><big><math> \; {\bf {\color{Red} {\downarrow}}} </math></big></big> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <!-- Lektion 30: --> | ||
| + | == <b><span style="color:#931136">4.2 Primitiva funktioner med villkor <math> \qquad\qquad\qquad\;\; </math> <small><small>Övningar: Boken, sid 177</small></small></span></b> == | ||
| + | |||
| + | I fysikaliska tillämpningar är den typiska formen av villkor <i>begynnelsevillkor</i>. Frågan är: | ||
| + | |||
| + | Vad gällde i början, dvs vilket vägmärke passerades vid <math> \, t = 0 \, </math>. Eller: Vad visade trippmätaren vid <math> \, t = 0 \, </math>? | ||
| + | |||
| + | |||
| + | <div class="ovnC"> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 2 Primitiva funktioner med villkor_30.jpg]] | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | Problemet ovan kallas även för en <i>differentialekvation med begynnelsevillkor</i> som kommer att behandlas i Matte 4 och 5. | ||
| + | |||
| + | |||
| + | <big><b><span style="color:#931136">Geometriskt exempel</span></b> på primitiv funktion med en annan typ av villkor<span style="color:black">:</span></big> | ||
| + | |||
| + | |||
| + | <div class="ovnE"> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 2a 177_Uppg_3326_30.jpg]] | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <!-- Lektion 31: --> | ||
| + | == <b><span style="color:#931136">4.3 Integral som area under kurvan <math> \qquad\qquad\qquad\;\; </math> <small><small>Övningar: Boken, sid 180</small></small></span></b> == | ||
| + | |||
| + | I början av <b><span style="color:red">Analysen</span></b> <math>-</math> den gren av matematiken som handlar om derivator och integraler och som på 1700-talet utvecklades av [https://sv.wikipedia.org/wiki/Isaac_Newton <b><span style="color:blue">Newton</span></b>] och [https://sv.wikipedia.org/wiki/Gottfried_Wilhelm_von_Leibniz <b><span style="color:blue">Leibniz</span></b>] <math>-</math> stod bl.a. följande frågeställning (se även [[2.4_Derivatans_definition#Fr.C3.A5n_sekanten_till_tangenten|<b><span style="color:blue">Derivatans definition</span></b>]]): | ||
| + | |||
| + | |||
| + | <div class="border-divblue"> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 3 Integraler_25.jpg]] | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <div class="border-divblue"> | ||
| + | <math> \displaystyle \, \int\limits_a^b f(x) \, dx </math> läses "Integralen över <math> f(x) \; dx \, </math> från <math> \, a \, </math> till <math> \, b \, </math>". <math> \, f(x) \, </math> kallas för <b><span style="color:red">integranden</span></b>. | ||
| + | |||
| + | <math> \, a \, </math> och <math> \, b \, </math> kallas för <b><span style="color:red">integrationsgränser</span></b> och ersätter integrationskonstanten <math> \, C \, </math>. | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <div class="ovnE"> | ||
| + | <small> <math> \displaystyle \, \int\limits_a^b f(x) \, dx </math> kallas för <b><span style="color:red">bestämd integral</span></b>. Dess resultat är ett tal. | ||
| + | |||
| + | <math> \displaystyle \, \int\limits f(x) \, dx </math> kallas för <b><span style="color:red">obestämd integral</span></b> vars resultat är en primitiv funktion med en integrationskonstant <math> \, C \, </math>. | ||
| + | |||
| + | För att bestämma integrationskonstanten måste ett villkor (begynnelsevillkor) vara givet. | ||
| + | </small></div> | ||
| + | |||
| + | |||
| + | <big><b><span style="color:#931136">Fysikaliskt exempel: </span></b> <math> \quad </math> <b><span style="color:#931136">Likformig rörelse med <span style="color:red">konstant</span> hastighet 60 km/h </span></b></big> | ||
| + | |||
| + | :::[[Image: Integral = Area_70.jpg]] | ||
| + | |||
| + | <math> \qquad\; v\,\text{-}\,t</math> diagrammet (till vänster): Kör man med med <math> \, 60 \, </math> km/h i <math> \, 4 \, </math> timmar har man kört en sträcka på <math> \, 60 \cdot 4 = 240 \, </math> km. | ||
| + | |||
| + | <math> \qquad\; \text{Sträckan} \, 240 \, = \, \text{Arean under hastighetskurvan} \, = \, \text{Integralen} \, \displaystyle \int\limits_0^4 \color{Red}{60} \, dt \, = \, \left[ \, \color{Red}{60\,t} \, \right]_0^4 \, = \, 60\cdot4 \, - \, 60\cdot0 \, = \, 240 </math> | ||
| + | |||
| + | <math> \qquad\; </math>Generellt: | ||
| + | |||
| + | <div class="border-divblue"> | ||
| + | Integralen över hastigheten = Arean under hastighetskurvan = Sträckan. | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <big><b><span style="color:#931136">Rörelse med <span style="color:red">variabel</span> hastighet (konstant acceleration):</span></b></big> | ||
| + | |||
| + | |||
| + | <div class="ovnC"> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 3a Integral som area under kurvan_30.jpg]] | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <!-- Lektion 32: | ||
| + | == <b><span style="color:#931136">4.4 Beräkning av integraler <math> \qquad\qquad\qquad\;\; </math> <small><small>Övningar: Boken, sid 185</small></small></span></b> == --> | ||
| + | == <b><span style="color:#931136">3.2 Integralberäkningar</span></b> == | ||
| + | <div class="ovnE"> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4 Integralberakning 20b.jpg]] | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <big>I övningarna finns även exponentialfunktioner vars primitiva funktioner sökes. Reglerna för dem skiljer sig från [[Kapitel_4_Integraler#Integrationsregeln_f.C3.B6r_en_potens:|<b><span style="color:blue">integrationsregeln för en potens</span></b>]]:</big> | ||
| + | |||
| + | |||
| + | <table> | ||
| + | <tr> | ||
| + | <td><div class="border-divblue"> | ||
| + | ==== <b><span style="color:#931136">Integrationsregler för exponentialfunktioner:</span></b> ==== | ||
| + | ---- | ||
| + | Om <math> \; f(x) \, = \; e\,^{k\,x} \qquad {\rm där} \qquad\, k = {\rm const.} </math> | ||
| + | |||
| + | då är den primitiva funktionen <math> \displaystyle \;\; F(x) \, = \, \boxed{\frac{e\,^{k\,x}}{k} \, + \, C\;} \; </math> | ||
| + | ---- | ||
| + | Om <math> \; f(x) \, = \; a\,^{k\,x} \qquad {\rm där} \qquad\, a, k = {\rm const.} </math> | ||
| + | |||
| + | då är den primitiva funktionen <math> \displaystyle \;\; F(x) \, = \, \boxed{\frac{a\,^{k\,x}}{k\,\ln a} \, + \, C\;} \; </math> | ||
| + | </div> | ||
| + | |||
| + | </td> | ||
| + | <td><math> \quad </math></td> | ||
| + | <td> | ||
| + | <div class="ovnE"> | ||
| + | <b><span style="color:#931136">Exempel:</span></b> | ||
| + | ---- | ||
| + | Om <math> \, f(x) \, = \, e\,^{4x} \; </math> då är den primitiva funktionen<span style="color:black">:</span> | ||
| + | |||
| + | ::<math> \, F(x) \, = \, \frac{e\,^{4x}}{4} + C \, = \, \frac{1}{4} \, e\,^{4x} + C</math> | ||
| + | ---- | ||
| + | Om <math> \, f(x) \, = \, 2\,^{3x} \; </math> då är den primitiva funktionen<span style="color:black">:</span> | ||
| + | |||
| + | ::<math> \, F(x) \, = \, \frac{2\,^{3x}}{3\,\ln 2} + C \, = \, \frac{1}{3\,\ln 2} \, 2\,^{3x} + C </math></div></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | |||
| + | <big>Beakta skillnaden mellan potensfunktioner (<math> x </math> i basen) och exponentialfunktioner (<math> x </math> i exponenten). Därav olika integrationsregler.</big> | ||
| + | |||
| + | ====== <div class="border-divblue"><b><span style="color:#931136">Övningar till 3.2 Integralberäkningar: Boken, sid 156-158</span></b></div> ====== | ||
<br> | <br> | ||
| + | <!-- Lektion 33: | ||
| + | == <b><span style="color:#931136">4.5 Användning av integraler <math> \qquad\qquad\qquad\;\; </math> <small><small>Övningar: Boken, sid 188-90</small></small></span></b> == --> | ||
| + | |||
| + | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| + | | style="border-bottom:1px solid #797979" width="5px" | | ||
| + | {{Not selected tab|[https://matte4.mathonline.se/index.php/Diagnosprov_kap_2/3_Derivator_%26_integraler <b>Diagnos kap 2/3 Der. & int.</b>]}} | ||
| + | | style="border-bottom:1px solid #797979" width="100%"| | ||
| + | |} | ||
| + | |||
| + | == <b><span style="color:#931136">3.5 Tillämpning av integraler</span></b> == | ||
| + | |||
| + | == <b><span style="color:#931136">Ett fysikaliskt exempel</span></b> == | ||
| + | <div class="ovnE"> | ||
| + | ==== <b><span style="color:#931136">Fallskärmshopp</span></b> ==== | ||
| + | |||
| + | En fallskärmshoppare faller fritt utan att öppna fallskärmen med hastigheten<span style="color:black">:</span> | ||
| + | |||
| + | <math> \qquad\qquad\qquad\qquad v(t) = 80\,(1 - 0,88\,^t) </math> | ||
| + | |||
| + | där <math> \, t = \, </math> tiden i sek och <math> \, v \, </math> hastigheten i meter/sek. | ||
| + | |||
| + | a) Bestäm hopparens maximala hastighet genom att: | ||
| + | |||
| + | rita grafen <math> \, v = v(t) \, </math> och tolka rörelsen fysikaliskt. | ||
| + | |||
| + | b) Formulera och lös problemet matematiskt och besvara frågan: | ||
| + | |||
| + | Hur långt har hopparen fallit när <math> \, v = 40 \, </math> m/s ? | ||
| + | </div> | ||
| + | |||
| + | |||
| + | === <b><span style="color:#931136">Fysikalisk tolkning</span></b> === | ||
| + | <div class="border-divblue"> | ||
| + | |||
| + | <table> | ||
| + | <tr> | ||
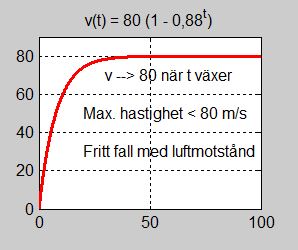
| + | <td>a) Grafen till <math> \, v = v(t) \, </math> visar att det finns en maximal hastighet som | ||
| + | |||
| + | fallskärmshopparen inte kan överskrida<span style="color:black">:</span> <math> \quad\;\; v_{max} = 80 </math> m/s | ||
| + | |||
| + | Efter ett tag når hopparen denna maximala hastighet, | ||
| + | |||
| + | enligt grafen efter ca. 40 sek. Algebraiskt<span>:</span> | ||
| + | |||
| + | <math> v_{max} = \displaystyle \lim_{t \to \infty}{(80(1 - 0,88^t))} = \lim_{t \to \infty}{(80 - \color{Red}{80\cdot0,88\,^t})} = 80 \quad </math> | ||
| + | |||
| + | Detta pga<span style="color:black">:</span> <math> \quad \displaystyle \lim_{t \to \infty}\,{(\color{Red}{80\cdot0,88\,^t})} \, = \, 0 \quad </math> och <math> \quad 0,88 \, < \, 1 </math>. | ||
| + | |||
| + | Efter att ha nått <math> \, \approx \, v_{max} \, </math> faller hopparen med konstant hastighet, | ||
| + | |||
| + | eftersom Luftmotstånd <math> \, \approx \, </math> Gravitation <math> \Rightarrow </math> <div class="smallBox">Fritt fall med luftmotstånd</div> | ||
| + | </td> | ||
| + | <td>[[Image: 5 186 Uppg 3438 Fritt falla.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | Enligt [https://www.naturvetenskap.org/fysik/gymnasiefysik/kraft/newtons-1a-lag/ <b><span style="color:blue">Newtons fösta lag:</span></b>] "Ett föremål är i vila eller rör sig med konstant hastighet, om och endast om | ||
| + | |||
| + | :::::::: summan av alla krafter <math> = 0 </math>." | ||
| + | </div> | ||
| + | |||
| + | |||
| + | === <b><span style="color:#931136">Matematisk formulering</span></b> === | ||
| + | <div class="ovnC"> | ||
| + | |||
| + | b) <u>Givet:</u> Hastigheten <math> \; s'(t) \, = \, v(t) \, = \, 80\,(1 - 0,88\,^t) </math> | ||
| + | |||
| + | <math> \qquad\qquad </math> Begynnelsevillkor<span style="color:black">:</span> <math> \, s(0) \, = \, 0 </math> | ||
| + | |||
| + | <u>Sökt:</u> 1. Funktionen <math> \displaystyle \quad\; s(t) \, = \, \int_0^t 80\,(1 - 0,88\,^t) \; dt </math> | ||
| + | |||
| + | 2. Sträckan <math> \quad\;\;\;\, s(t_1) \, </math>, där <math> \; v(t_1) \, = \, 40 \, </math> m/s | ||
| + | </div> | ||
| + | |||
| + | |||
| + | === <b><span style="color:#931136">Matematisk lösning</span></b> === | ||
| + | <div class="ovnC"> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 5 186 Uppg 3438 Fritt fall_800.jpg]]</div> | ||
| + | |||
| + | |||
| + | <big><b>Övning:</b> Rita grafen <math> \, s = s(t) \, </math> och tolka med hjälp av den resultaten ovan.</big> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | == <b><span style="color:#931136">Ett samhällsvetenskapligt exempel</span></b> == | ||
| + | <div class="ovnE"> | ||
| + | ==== <b><span style="color:#931136">Röster i melodifestivalen</span></b> ==== | ||
| + | |||
| + | Antalet inkommande röster per minut i melodifestivalen beskrivs av funktionen<span style="color:black">:</span> | ||
| + | |||
| + | <math> \qquad\qquad\qquad\qquad r(x)\, = \, 14\,500\,x \, - \, 150\,x^2 </math> | ||
| + | |||
| + | där <math> \,\, r \,\, </math> är antalet inkommande röster per minut | ||
| + | |||
| + | och <math> \, x \, </math> tiden i minuter efter röstningens start. | ||
| + | |||
| + | Totalt kom in <math> \, 14,5 \, </math> miljoner röster under röstningsperioden. | ||
| + | |||
| + | Beräkna hur länge röstningen pågick. | ||
| + | |||
| + | Kontrollera ditt resultat med grafräknarens verktyg för numerisk integration. | ||
| + | </div> | ||
| + | |||
| + | |||
| + | === <b><span style="color:#931136">Lösning</span></b> === | ||
| + | <div class="border-divblue"> | ||
| + | <!-- ==== <span style="color:#931136">Antalet röster som integral</span> ==== --> | ||
| + | <math> r(x) \, = \, </math> antalet inkommande röster <b><span style="color:red">per minut</span></b>. | ||
| + | |||
| + | Vi inför <math> \, R(x) \, = \, </math> antalet (summan) röster som kommit in vid tidpunkten <math> \, x \, </math>. | ||
| + | |||
| + | Då blir <math> \, r(x) \, </math> rösternas tillväxthastighet (antal per min) dvs derivatan av <math> \, R(x) \, </math><span>:</span> | ||
| + | |||
| + | ::::::::<math> \qquad\qquad R\,'(x) \, = \, r(x) </math> | ||
| + | |||
| + | vilket betyder att <math> \, R(x) \, </math> är den primitiva funktionen till <math> \, r(x) \, </math><span style="color:black">:</span> | ||
| + | |||
| + | <math> \qquad R\,'(x) \, = \, r(x) \, = \, 14\,500\,x \, - \, 150\,x^2 </math> | ||
| + | |||
| + | Vi integrerar ekvationen ovan och sätter den till <math> \, 14,5 \, </math> miljoner inkommande röster <span>:</span> | ||
| + | |||
| + | <math> \qquad \displaystyle R(t) \, = \, \int_0^t (14\,500\,x - 150\,x^2) \; dx \, = \, 14\,500\,000 </math> | ||
| + | |||
| + | <math> \qquad\qquad\qquad\; \displaystyle \left[ \, \frac{14\,500\,x^2}{2} - \frac{150\,x^3}{3} \, \right]_0^t \, = \, 14\,500\,000 </math> | ||
| + | |||
| + | <math> \qquad \left[ \, 7\,250\,x^2 - 50\,x^3 \, \right]_0^t \, = \, 7\,250\,t^2 - 50\,t^3 \, = \, 14\,500\,000 </math> | ||
| + | |||
| + | <math> \qquad 7\,250\,t^2 - 50\,t^3 - 14\,500\,000 \, = \, 0 </math> | ||
| + | |||
| + | <math> \qquad 50\,t^3 - 7\,250\,t^2 + 14\,500\,000 \, = \, 0 </math> | ||
| + | |||
| + | Grafräknarens [[Grafritning_och_ekvationslösning_med_räknare#Ekvationsl.C3.B6sning_med_minir.C3.A4knare|<b><span style="color:blue">ekvationslösare</span></b>]] ger<span style="color:black">:</span> <math> \qquad t \, \approx \, 57,6041146 </math> | ||
| + | |||
| + | <math> 0,6041146 \, </math> minuter är <math> \, 0,6041146 \cdot 60 \, \approx \ 36,25 \, </math> sekunder. | ||
| + | |||
| + | Röstningen pågick i <math> \, \underline{57\,\,{\rm minuter\;och\;} 36\,\,{\rm sekunder.}} </math> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | === <b><span style="color:#931136">Kontroll</span></b> === | ||
| + | |||
| + | <big> | ||
| + | Vi beräknar med grafräknaren <math> \, \displaystyle \int_0^{57,6041146} (14\,500\,x - 150\,x^2) \; dx \, </math> och kontrollerar om det blir <math> \, 14\,500\,000 \, </math>. | ||
| + | |||
| + | Beskrivningen bygger på grafräknaren TI-82 STATS, men kan med lite modifikation tillämpas på alla grafräknare. | ||
| + | </big> | ||
| + | |||
| + | |||
| + | == <b><span style="color:#931136">Numerisk integration med miniräknare</span></b> == | ||
| + | <div class="border-divblue"> | ||
| + | Tryck i miniräknaren på knappen MATH. | ||
| + | |||
| + | Gå med piltangenten till <b> fnInt( </b> som står för <b>n</b>umerical <b>Int</b>egration. | ||
| + | |||
| + | Tryck på ENTER. | ||
| + | |||
| + | Mata in så att det efteråt står följande i displayen<span style="color:black">:</span> | ||
| + | |||
| + | :::<b> fnInt ( 14500X-150X^2, X, 0, 57.6041146 ) </b> | ||
| + | |||
| + | Tryck på ENTER. I displayen visas <math> \underline{14\,500\,000} </math>, vilket betyder<span style="color:black">:</span> | ||
| + | |||
| + | <math> \qquad \displaystyle \int_0^{57,6041146} (14\,500\,x - 150\,x^2) \; dx \, = \, 14\,500\,000 </math> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <big> | ||
| + | Räknarens funktion <b> fnInt( ) </b> tar fyra argument separerade med komma: | ||
| + | |||
| + | 1) Integrandens funktionsuttryck <math> \, f(x) \, </math>, i exemplet ovan <math> r(x) </math>. | ||
| + | |||
| + | 2) Variabeln med avseende på vilken <math> f(x) </math> ska integreras. | ||
| + | |||
| + | 3) Den undre integrationsgränsen. | ||
| + | |||
| + | 4) Den övre integrationsgränsen. | ||
| + | </big> | ||
| + | |||
| + | |||
| + | == <b><span style="color:#931136">Ett ekonomiskt exempel</span></b> == | ||
| + | <div class="ovnE"> | ||
| + | ==== <b><span style="color:#931136">Marginalkostnad</span></b> ==== | ||
| + | <b><span style="color:#931136">som derivatan av kostnaden</span></b> (jfr. med [[2.2_Genomsnittlig_förändringshastighet#Exempel_1_Marginalskatt|<b><span style="color:blue">marginalskatt</span></b>)]] | ||
<br> | <br> | ||
| + | <b><span style="color:#931136">Kostnaden K som en funktion av mängden x (antalet broschyrer)</span></b> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 5 189 Uppg 3433 Marginalkostnad.jpg]] | ||
| + | </div> | ||
| + | </div> | ||
| + | <!-- | ||
| + | == <b><span style="color:#931136">Appendix: Integralens definition</span></b> == | ||
| + | <div class="ovnC"> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4 Int_Limes_Summa_30a.jpg]] | ||
| + | </div> | ||
| + | </div> | ||
| − | + | ||
| + | Se även animationen i Figure 8.6.1 på [https://www.whitman.edu/mathematics/calculus_online/section08.06.html <b><span style="color:blue">webben</span></b>]. | ||
| + | --> | ||
| + | |||
| + | ====== <div class="border-divblue"><b><span style="color:#931136">Övningar till 3.5 Tillämpning av integraler: Boken, sid 169-172</span></b></div> ====== | ||
| + | |||
| + | <br><br> | ||
| + | |||
| + | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| + | | style="border-bottom:1px solid #797979" width="5px" | | ||
| + | {{Not selected tab|[https://matte4.mathonline.se/index.php/Diagnosprov_kap_2/3_Derivator_%26_integraler <b>Diagnos kap 2/3 Der. & int.</b>]}} | ||
| + | | style="border-bottom:1px solid #797979" width="100%"| | ||
| + | |} | ||
| + | </big> | ||
| − | |||
| − | |||
| − | [[Matte:Copyrights|Copyright]] © 2011- | + | [[Matte:Copyrights|Copyright]] © 2011-2025 Lieta AB. All Rights Reserved. |
Nuvarande version från 7 januari 2025 kl. 11.42
| Genomgångar | Formelsamling Integraler | Diagnos kap 2/3 Der. & int. |
F.o.m. detta kapitel finns kursens övningar inte på webben (pga tidsbrist). Därför: Läs igenom genomgångarna här, men använd för
övningarna boken (Matematik 5000). Leta i bokens innehållsförteckning och register efter resp. kapitlets/avsnittets övningar.
Tyvärr överensstämmer sidouppgifterna här inte med boken.
4.1 Primitiva funktioner \( \qquad\qquad\qquad\;\; \) Övningar: Boken, sid 175
Hittills: En funktion var given. Vi sökte funktionens derivata. Nu vänder vi på steken:
Det omvända problemet:
OBS! Annan problemställning och annan beteckning:
\( \; f\,(x) \, \) är inte längre en given funktion som vi ska derivera.
\( \; f\,(x) \, \) är en given derivata av en okänd funktion \( \, \color{red} {F\,(x)} \, \) som vi söker, dvs \( \, \color{red} {F\,'(x)} = f\,(x) \, \).
Exempel 1:
Givet: \( \quad\;\; f\,(x) \, = \, 2\,x \, = \, \) Derivatan av någon funktion
Sökt: \( \quad\;\;\, F(x) \quad \) så att \( \quad F\,'(x) = 2\,x \)
Lösning: \( \;\; F(x) = \boxed{\textstyle x\,^2 \, + C\,} \, , \;\; C={\rm const.} \)
Kontroll: \( \;\; F\,'(x) = 2\,x + 0 \, = \, 2\,x \, = \, f\,(x) \)
Att hitta en primitiv funktion kallas för integration och \( \, C \, \) för integrationskonstanten.
Exempel 2: Givet: \( \quad\;\; f\,(x) \, = \, x\,^3 + 5 \, = \, \) Derivatan av någon funktion Sökt: \( \quad\;\;\, F(x) \quad \) så att \( \quad F\,'(x) = x\,^3 + 5 \) Lösning: \( \;\; F(x) = \boxed{\textstyle \frac{1}{4} x\,^4 + 5 \, x + C\,} \, , \;\; C={\rm const.} \) Kontroll: \( \;\; F\,'(x) = \frac{4}{4} x\,^3 + 5 + 0 \, = \, x\,^3 + 5 \, = \, f\,(x) \) |
\( \quad \) | Allmän definition: Givet: \( \quad f\,(x) \) Sökt: \( \quad \) En funktion \( \;\; F\,(x) \;\; \) så att: \( \qquad\qquad\quad\; \boxed{F\,'\,(x) = f\,(x)} \) Funktionen \( \, F\,(x) \, \) kallas för primitiv funktion. |
- Integration är deriveringens inversa (omvända) operation. Därför:
- Integrationsregler för olika funktionstyper följer genom att vända om deriveringsreglerna. T.ex.:
Integrationsregeln för en potens:Om \( f(x) = x\,^n \qquad {\rm där} \qquad\, n = {\rm const.} \neq -1\) då \(\; F(x) = \boxed{\frac{x\,^{n+1}}{n+1} \, + \, C\;} \;, C = \) integrationskonstanten |
\( \quad \) |
Exempel: För \( \, f(x) \, = \, x^4 \; \) blir den primitiva funktionen:
|
- Bevis: \( \, F\,'(x) = \displaystyle \frac{(n+1) \, x\,^{n+1-1}}{n+1} \, + \, 0 \, = \, \frac{(n+1) \, x\,^{n}}{n+1} = x\,^n = f\,(x) \qquad \) Exempel: \( \;\; F\,'(x) \, = \, \displaystyle \frac{5}{5} \, x\,^4 \, + \, 0 \, = \, x\,^4 \, = \, f\,(x) \qquad \)
- Regeln ovan gäller inte bara för positiva \( \, n \, \) utan även för negativa (undantaget \( -1 \)) och rationella exponenter.
- Ytterligare regler om primitiva funktioner (för exponentialfunktioner) anges senare.
Fysikalisk tolkning:
| \( \quad \) |  |
\( \quad \) Hastighetsmätaren deriverar. \( \;\; \)
|
\( \quad \)  |
Integration är den inversa operationen till derivering. \( \quad \) Primitiv funktion = "Anti"derivata
Derivata Integral Fysikalisk tolkning: Hastighet Sträcka Geometrisk tolkning: Kurvans lutning Area under kurvan Matematisk tolkning: Limes av differenskvot Limes av oändlig summa
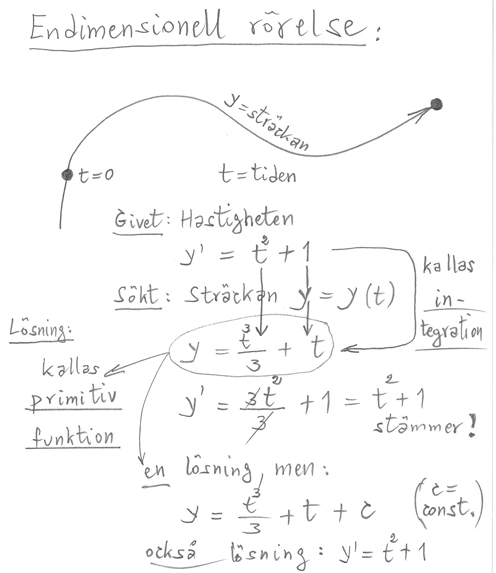
Integrationskonstanten \( \, C \, \):
Om en given funktion har en primitiva funktion så har den pga \( \, C={\rm const.} \, \) oändligt
många primitiva funktioner.
För att få endast en primitiv funktion \( \, F(x) \, \) ställs vissa villkor på \( \, F(x) \, \). I fysiken kallas
de för begynnelsevillkor. Villkoren används för att bestämma integrationskonstanten \( \, C \, \). \( \; {\bf {\color{Red} {\downarrow}}} \)
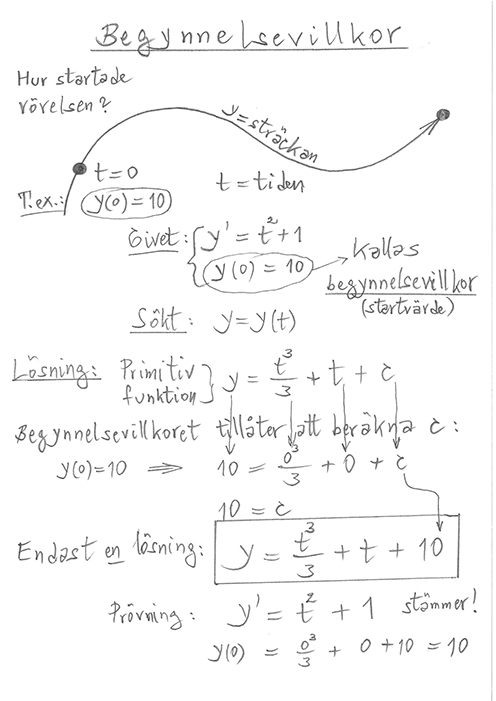
4.2 Primitiva funktioner med villkor \( \qquad\qquad\qquad\;\; \) Övningar: Boken, sid 177
I fysikaliska tillämpningar är den typiska formen av villkor begynnelsevillkor. Frågan är:
Vad gällde i början, dvs vilket vägmärke passerades vid \( \, t = 0 \, \). Eller: Vad visade trippmätaren vid \( \, t = 0 \, \)?
Problemet ovan kallas även för en differentialekvation med begynnelsevillkor som kommer att behandlas i Matte 4 och 5.
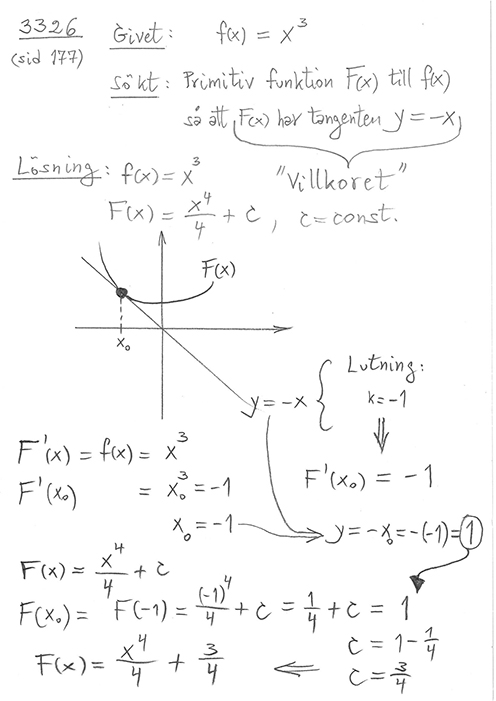
Geometriskt exempel på primitiv funktion med en annan typ av villkor:
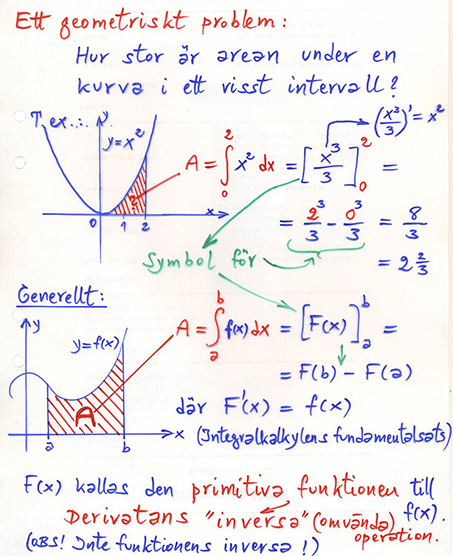
4.3 Integral som area under kurvan \( \qquad\qquad\qquad\;\; \) Övningar: Boken, sid 180
I början av Analysen \(-\) den gren av matematiken som handlar om derivator och integraler och som på 1700-talet utvecklades av Newton och Leibniz \(-\) stod bl.a. följande frågeställning (se även Derivatans definition):
\( \displaystyle \, \int\limits_a^b f(x) \, dx \) läses "Integralen över \( f(x) \; dx \, \) från \( \, a \, \) till \( \, b \, \)". \( \, f(x) \, \) kallas för integranden.
\( \, a \, \) och \( \, b \, \) kallas för integrationsgränser och ersätter integrationskonstanten \( \, C \, \).
\( \displaystyle \, \int\limits_a^b f(x) \, dx \) kallas för bestämd integral. Dess resultat är ett tal.
\( \displaystyle \, \int\limits f(x) \, dx \) kallas för obestämd integral vars resultat är en primitiv funktion med en integrationskonstant \( \, C \, \).
För att bestämma integrationskonstanten måste ett villkor (begynnelsevillkor) vara givet.
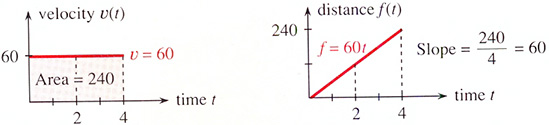
Fysikaliskt exempel: \( \quad \) Likformig rörelse med konstant hastighet 60 km/h
\( \qquad\; v\,\text{-}\,t\) diagrammet (till vänster): Kör man med med \( \, 60 \, \) km/h i \( \, 4 \, \) timmar har man kört en sträcka på \( \, 60 \cdot 4 = 240 \, \) km.
\( \qquad\; \text{Sträckan} \, 240 \, = \, \text{Arean under hastighetskurvan} \, = \, \text{Integralen} \, \displaystyle \int\limits_0^4 \color{Red}{60} \, dt \, = \, \left[ \, \color{Red}{60\,t} \, \right]_0^4 \, = \, 60\cdot4 \, - \, 60\cdot0 \, = \, 240 \)
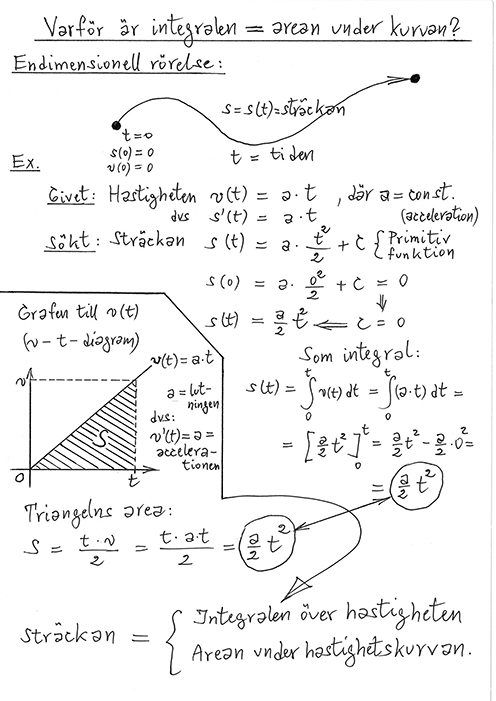
\( \qquad\; \)Generellt:
Integralen över hastigheten = Arean under hastighetskurvan = Sträckan.
Rörelse med variabel hastighet (konstant acceleration):
3.2 Integralberäkningar
I övningarna finns även exponentialfunktioner vars primitiva funktioner sökes. Reglerna för dem skiljer sig från integrationsregeln för en potens:
Integrationsregler för exponentialfunktioner:Om \( \; f(x) \, = \; e\,^{k\,x} \qquad {\rm där} \qquad\, k = {\rm const.} \) då är den primitiva funktionen \( \displaystyle \;\; F(x) \, = \, \boxed{\frac{e\,^{k\,x}}{k} \, + \, C\;} \; \) Om \( \; f(x) \, = \; a\,^{k\,x} \qquad {\rm där} \qquad\, a, k = {\rm const.} \) då är den primitiva funktionen \( \displaystyle \;\; F(x) \, = \, \boxed{\frac{a\,^{k\,x}}{k\,\ln a} \, + \, C\;} \; \) |
\( \quad \) |
Exempel: Om \( \, f(x) \, = \, e\,^{4x} \; \) då är den primitiva funktionen:
Om \( \, f(x) \, = \, 2\,^{3x} \; \) då är den primitiva funktionen:
|
Beakta skillnaden mellan potensfunktioner (\( x \) i basen) och exponentialfunktioner (\( x \) i exponenten). Därav olika integrationsregler.
Övningar till 3.2 Integralberäkningar: Boken, sid 156-158
| Diagnos kap 2/3 Der. & int. |
3.5 Tillämpning av integraler
Ett fysikaliskt exempel
Fallskärmshopp
En fallskärmshoppare faller fritt utan att öppna fallskärmen med hastigheten:
\( \qquad\qquad\qquad\qquad v(t) = 80\,(1 - 0,88\,^t) \)
där \( \, t = \, \) tiden i sek och \( \, v \, \) hastigheten i meter/sek.
a) Bestäm hopparens maximala hastighet genom att:
rita grafen \( \, v = v(t) \, \) och tolka rörelsen fysikaliskt.
b) Formulera och lös problemet matematiskt och besvara frågan:
Hur långt har hopparen fallit när \( \, v = 40 \, \) m/s ?
Fysikalisk tolkning
Enligt Newtons fösta lag: "Ett föremål är i vila eller rör sig med konstant hastighet, om och endast om
- summan av alla krafter \( = 0 \)."
Matematisk formulering
b) Givet: Hastigheten \( \; s'(t) \, = \, v(t) \, = \, 80\,(1 - 0,88\,^t) \)
\( \qquad\qquad \) Begynnelsevillkor: \( \, s(0) \, = \, 0 \)
Sökt: 1. Funktionen \( \displaystyle \quad\; s(t) \, = \, \int_0^t 80\,(1 - 0,88\,^t) \; dt \)
2. Sträckan \( \quad\;\;\;\, s(t_1) \, \), där \( \; v(t_1) \, = \, 40 \, \) m/s
Matematisk lösning
Ett samhällsvetenskapligt exempel
Röster i melodifestivalen
Antalet inkommande röster per minut i melodifestivalen beskrivs av funktionen:
\( \qquad\qquad\qquad\qquad r(x)\, = \, 14\,500\,x \, - \, 150\,x^2 \)
där \( \,\, r \,\, \) är antalet inkommande röster per minut
och \( \, x \, \) tiden i minuter efter röstningens start.
Totalt kom in \( \, 14,5 \, \) miljoner röster under röstningsperioden.
Beräkna hur länge röstningen pågick.
Kontrollera ditt resultat med grafräknarens verktyg för numerisk integration.
Lösning
\( r(x) \, = \, \) antalet inkommande röster per minut.
Vi inför \( \, R(x) \, = \, \) antalet (summan) röster som kommit in vid tidpunkten \( \, x \, \).
Då blir \( \, r(x) \, \) rösternas tillväxthastighet (antal per min) dvs derivatan av \( \, R(x) \, \):
- \[ \qquad\qquad R\,'(x) \, = \, r(x) \]
vilket betyder att \( \, R(x) \, \) är den primitiva funktionen till \( \, r(x) \, \):
\( \qquad R\,'(x) \, = \, r(x) \, = \, 14\,500\,x \, - \, 150\,x^2 \)
Vi integrerar ekvationen ovan och sätter den till \( \, 14,5 \, \) miljoner inkommande röster :
\( \qquad \displaystyle R(t) \, = \, \int_0^t (14\,500\,x - 150\,x^2) \; dx \, = \, 14\,500\,000 \)
\( \qquad\qquad\qquad\; \displaystyle \left[ \, \frac{14\,500\,x^2}{2} - \frac{150\,x^3}{3} \, \right]_0^t \, = \, 14\,500\,000 \)
\( \qquad \left[ \, 7\,250\,x^2 - 50\,x^3 \, \right]_0^t \, = \, 7\,250\,t^2 - 50\,t^3 \, = \, 14\,500\,000 \)
\( \qquad 7\,250\,t^2 - 50\,t^3 - 14\,500\,000 \, = \, 0 \)
\( \qquad 50\,t^3 - 7\,250\,t^2 + 14\,500\,000 \, = \, 0 \)
Grafräknarens ekvationslösare ger: \( \qquad t \, \approx \, 57,6041146 \)
\( 0,6041146 \, \) minuter är \( \, 0,6041146 \cdot 60 \, \approx \ 36,25 \, \) sekunder.
Röstningen pågick i \( \, \underline{57\,\,{\rm minuter\;och\;} 36\,\,{\rm sekunder.}} \)
Kontroll
Vi beräknar med grafräknaren \( \, \displaystyle \int_0^{57,6041146} (14\,500\,x - 150\,x^2) \; dx \, \) och kontrollerar om det blir \( \, 14\,500\,000 \, \).
Beskrivningen bygger på grafräknaren TI-82 STATS, men kan med lite modifikation tillämpas på alla grafräknare.
Numerisk integration med miniräknare
Tryck i miniräknaren på knappen MATH.
Gå med piltangenten till fnInt( som står för numerical Integration.
Tryck på ENTER.
Mata in så att det efteråt står följande i displayen:
- fnInt ( 14500X-150X^2, X, 0, 57.6041146 )
Tryck på ENTER. I displayen visas \( \underline{14\,500\,000} \), vilket betyder:
\( \qquad \displaystyle \int_0^{57,6041146} (14\,500\,x - 150\,x^2) \; dx \, = \, 14\,500\,000 \)
Räknarens funktion fnInt( ) tar fyra argument separerade med komma:
1) Integrandens funktionsuttryck \( \, f(x) \, \), i exemplet ovan \( r(x) \).
2) Variabeln med avseende på vilken \( f(x) \) ska integreras.
3) Den undre integrationsgränsen.
4) Den övre integrationsgränsen.
Ett ekonomiskt exempel
Marginalkostnad
som derivatan av kostnaden (jfr. med marginalskatt)
Kostnaden K som en funktion av mängden x (antalet broschyrer)
Övningar till 3.5 Tillämpning av integraler: Boken, sid 169-172
| Diagnos kap 2/3 Der. & int. |
Copyright © 2011-2025 Lieta AB. All Rights Reserved.