Skillnad mellan versioner av "2.7 Numerisk derivering"
Taifun (Diskussion | bidrag) m (→Varför numerisk derivering?) |
Taifun (Diskussion | bidrag) m (→Varför numerisk derivering?) |
||
| Rad 20: | Rad 20: | ||
::Denna funktion kan inte deriveras med någon av de deriveringsregler vi känner till hittills. Senare i Matte D kommer vi att lära oss en regel, den s.k. kvotregeln med vars hjälp vi kan derivera funktionen ovan. | ::Denna funktion kan inte deriveras med någon av de deriveringsregler vi känner till hittills. Senare i Matte D kommer vi att lära oss en regel, den s.k. kvotregeln med vars hjälp vi kan derivera funktionen ovan. | ||
| − | ::* När vi har en funktion vars derivata blir så komlicerad att | + | ::* När vi har en funktion vars derivata blir så komlicerad att det tar mer tid att ställa upp den än att genomföra numerisk derivering. Exempel: |
:::::::::<math> f(x) = {\sin\,3\,x \over 4\,\cos\,x} </math> | :::::::::<math> f(x) = {\sin\,3\,x \over 4\,\cos\,x} </math> | ||
Versionen från 18 maj 2011 kl. 18.58
| Teori | Övningar |
Innehåll
Varför numerisk derivering?
Numerisk derivering är en metod för approximativ beräkning av derivatan. Med hjälp av numeriska deriveringsformler beräknas ett nämevärde för derivatan. Frågan uppstår: varför ska vi ta fram ett nämevärde när vi kan få derivatans exakta värde med hjälp av de deriveringsregler som vi sammanställde i en tabell i förra avsnitt? Svaret är: Ibland eller t.o.m. ofta kan vi inte det, vilket blir klarare om vi tittar på den numeriska deriveringens användningsområden.
Numerisk derivering används i följande situationer:
- När vi ska derivera en funktion som inte matchar mot någon funktionstyp i vår deriveringstabell. Ett exempel är:
- \[ f(x) = {2 \over e\,^x + 1} \]
- Denna funktion kan inte deriveras med någon av de deriveringsregler vi känner till hittills. Senare i Matte D kommer vi att lära oss en regel, den s.k. kvotregeln med vars hjälp vi kan derivera funktionen ovan.
- När vi har en funktion vars derivata blir så komlicerad att det tar mer tid att ställa upp den än att genomföra numerisk derivering. Exempel:
- \[ f(x) = {\sin\,3\,x \over 4\,\cos\,x} \]
- \[ f\,'(x) = {12\,\cos\,3\,x \cdot \cos\,x \,+\, 4\,\sin\,3\,x \cdot \sin\,x \over 16\,\cos^2\,x} \]
- För det första är det inte enkelt att ställa upp \( f\,'(x) \). Även detta görs med kvotregeln som vi inte känner till än.
- För det andra visar exemplet att det är väsentligt enklare att beräkna funktionsvärden av typ \( f(2)\, \) än t.ex. \( f\,'(2) \). I de numeriska deriveringsformlerna ingår endast beräkningar av funktionsvärden för \( f(x)\, \), inte för \( f\,'(x) \).
- Denna funktion saknar algebraisk formel. Ändå uppfyller den definitionen på en funktion, nämligen att vara en "regel som tilldelar varje \( x\, \)-värde endast ett \( y\, \)-värde."
- Pga avsaknaden av en formel finns det ingen annan möjlighet att derivera en sådan funktion än numerisk derivering.
Det finns en uppsjö av numeriska deriveringsformler. Vi behandlar i detta avsnitt de vanligaste:
- Framåtdifferenskvoten
- Bakåtdifferenskvoten
- Centrala differenskvoten
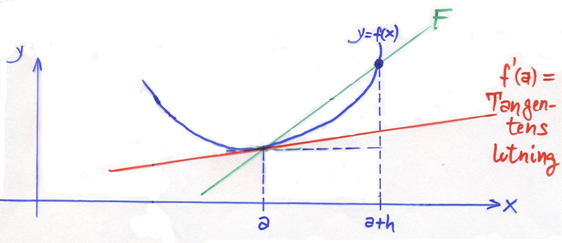
Framåtdifferenskvoten
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Framåtdifferenskvoten:
- Tangentens lutning \( \; = \; f\,'(a) \quad \approx \quad {f(a + h) \, - \, f(a) \over h} \; = \; \) Sekanten F:s lutning
Approximationen är desto bättre ju mindre \( h\, \) är.
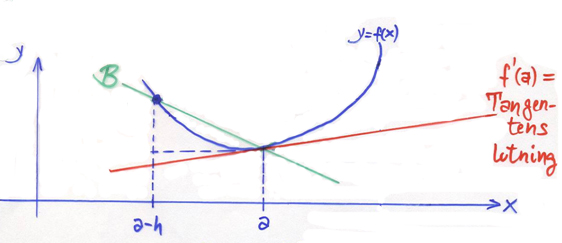
Bakåtdifferenskvoten
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Bakåtdifferenskvoten:
- Tangentens lutning \( \; = \; f\,'(a) \quad \approx \quad {f(a) \, - \, f(a-h) \over h} \; = \; \) Sekanten B:s lutning
Approximationen är desto bättre ju mindre \( h\, \) är.
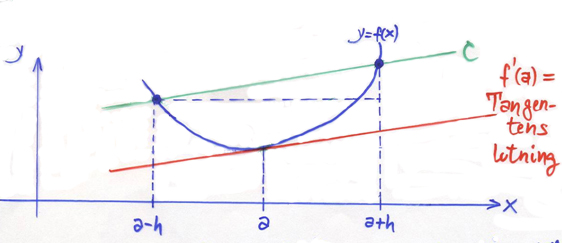
Centrala differenskvoten
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Centrala differenskvoten:
- Tangentens lutning \( \; = \; f\,'(a) \quad \approx \quad {f(a + h) \, - \, f(a-h) \over 2\,h} \; = \; \) Sekanten C:s lutning
Approximationen är desto bättre ju mindre \( h\, \) är.
Internetlänkar
http://www.youtube.com/watch?v=OyKmc2bPWe0
http://www.youtube.com/watch?v=8of_svLfcjk
http://www.youtube.com/watch?v=OY8CeLUxE64&feature=related
http://www.youtube.com/watch?v=2wH-g60EJ18&feature=related
http://www.larcentrum.org/Safir/MA1203W/htm/m03_deriv1/m03_deriv_definition.htm
http://www.naturvetenskap.org/index.php?option=com_content&view=article&id=129&Itemid=132
Copyright © 2010-2011 Taifun Alishenas. All Rights Reserved.