Skillnad mellan versioner av "2.7 Numerisk derivering"
Taifun (Diskussion | bidrag) m (→Exempel 3) |
Taifun (Diskussion | bidrag) m (→Exempel 3) |
||
| Rad 165: | Rad 165: | ||
<math> = {x^2 + 2\,x\,h + h^2 - x^2 + 2\,x\,h - h^2 \over 2\,h} = {4\,x\,h \over 2\,h} = 2\,x = f\,'(x) </math> | <math> = {x^2 + 2\,x\,h + h^2 - x^2 + 2\,x\,h - h^2 \over 2\,h} = {4\,x\,h \over 2\,h} = 2\,x = f\,'(x) </math> | ||
| − | Det räcker att bevisa satsen för <math> f(x) = x^2\, </math> som an slags representant för alla 2:a gradsfunktioner, eftersom <math> x^2\, </math> är den avgörande termen för 2:a gradsfunktioner. Självfallet går det att bevisa satsen även för <math> f(x) = a\,x^2 + b\,x + c </math>. Det tar bara lite längre att räkna. Rsultatet är det samma: Den centrala differenskvoten deriverar 2:a gradsfunktionerna exakt. | + | Det räcker att bevisa satsen för <math> f(x) = x^2\, </math> som an slags representant för alla 2:a gradsfunktioner, eftersom <math> x^2\, </math> är den avgörande termen för 2:a gradsfunktioner. Självfallet går det att bevisa satsen även för <math> f(x) = a\,x^2 + b\,x + c </math>. Det tar bara lite längre att räkna. Rsultatet är det samma: Den centrala differenskvoten deriverar 2:a gradsfunktionerna exakt. Att detta är oberoende av steglängden visas i beviset ovan genom att <math> h\, </math> kan förkortas bort i slutet. |
== Internetlänkar == | == Internetlänkar == | ||
Versionen från 19 maj 2011 kl. 18.30
| Teori | Övningar |
Innehåll
Varför numerisk derivering?
Numerisk derivering är en metod för approximativ (ungefärlig, nära men inte exakt) beräkning av derivatan. Med hjälp av numeriska deriveringsformler beräknas ett nämevärde för derivatan. Frågan uppstår: varför ska vi ta fram ett nämevärde när vi kan få derivatans exakta värde med hjälp av de deriveringsregler som vi sammanställde i en tabell i förra avsnitt? Svaret är: Ibland eller t.o.m. ofta kan vi inte göra det, vilket blir klarare om vi tittar på den numeriska deriveringens användningsområden.
Numerisk derivering används i följande situationer:
- När vi ska derivera en funktion som inte matchar mot någon funktionstyp i vår deriveringstabell. Ett exempel är:
- \[ f(x) = {2 \over e\,^x + 1} \]
- Denna funktion kan inte deriveras med någon av de deriveringsregler vi känner till hittills. Senare i Matte D kommer vi att lära oss den s.k. kvotregeln med vars hjälp funktionen ovan kan deriveras. Ett annat exempel är \( f(x) = \ln x\, \) vars numerisk derivering visas i Exempel 2 längre fram.
- När vi har en funktion vars derivata blir så komlicerad att det tar mer tid att ställa upp den än att genomföra numerisk derivering. Exempel:
- \[ f(x) = {\sin\,3\,x \over 4\,\cos\,x} \]
- \[ f\,'(x) = {12\,\cos\,3\,x \cdot \cos\,x \,+\, 4\,\sin\,3\,x \cdot \sin\,x \over 16\,\cos^2\,x} \]
- För det första är det inte enkelt att ställa upp \( f\,'(x) \). Även detta görs med kvotregeln som vi inte känner till än.
- För det andra visar exemplet att det är väsentligt enklare att beräkna funktionsvärden av typ \( f(2)\, \) än t.ex. \( f\,'(2) \). I de numeriska deriveringsformlerna ingår endast beräkningar av funktionsvärden för \( f(x)\, \), inte för \( f\,'(x) \).
- Sådana funktioner förekommer ofta som resultat av mätdata. De saknar algebraisk formel. Ändå uppfyller de definitionen på en funktion, nämligen att vara en
- "Regel som tilldelar varje \( x\, \)-värde endast ett \( y\, \)-värde."
- Pga avsaknaden av en formel finns det ingen annan möjlighet att derivera en sådan funktion än numerisk derivering.
Det finns en uppsjö av numeriska deriveringsformler. Vi behandlar i detta avsnitt de tre enklaste:
- Framåtdifferenskvoten
- Bakåtdifferenskvoten
- Centrala differenskvoten
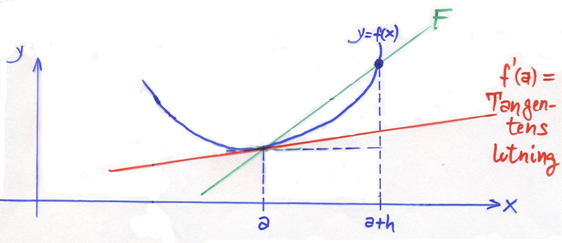
Framåtdifferenskvoten
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Framåtdifferenskvoten:
- Tangentens lutning \( \; = \; f\,'(a) \quad \approx \quad {f(a + h) \, - \, f(a) \over h} \; = \; \) Sekanten F:s lutning
\( h\, \) kallas steglängden. Approximationen är desto bättre ju mindre steglängden är.
Exempel 1
Givet:
- Följande funktion \( f(x)\, \) i tabellform:
\( x\, \) \( f(x)\, \) \( 0,5\, \) \( 1,79744\, \) \( 0,6\, \) \( 2,04424\, \) \( 0,7\, \) \( 2,32751\, \)
Sökt:
- Funktionens derivata i \( x = 0,6\, \) dvs \( f\,'(0,6) \) med framåtdifferenskvoten .
Lösning:
- \[ f\,'(0,6) \approx {f(0,6 + 0,1) - f(0,6) \over 0,1} = {f(0,7) - f(0,6) \over 0,1} = {2,32751 - 2,04424 \over 0,1} = {0,28327 \over 0,1} = 2,8327 \]
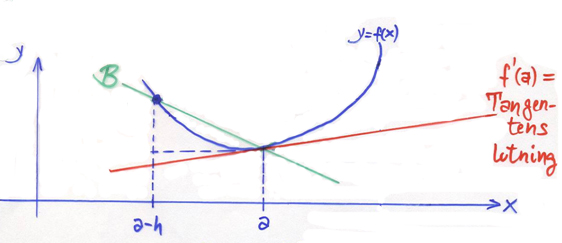
Bakåtdifferenskvoten
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Bakåtdifferenskvoten:
- Tangentens lutning \( \; = \; f\,'(a) \quad \approx \quad {f(a) \, - \, f(a-h) \over h} \; = \; \) Sekanten B:s lutning
Även här gäller att approximationen är desto bättre ju mindre steglängden \( h\, \) är.
Exempel 2
Givet:
- Funktionen \( f(x) = \ln x\, \)
- Steglängden \( h = 0,01\, \)
Sökt:
- Funktionens derivata i \( x = 1,8\, \) dvs \( f\,'(1,8) \) med bakåtdifferenskvoten .
Lösning:
- \[ f\,'(1,8) \approx {f(1,8) - f(1,8 - 0,01) \over 0,01} = {f(1,8) - f(1,79) \over 0,01} = {\ln(1,8) - \ln(1,79) \over 0,01} = 0,5571 \]
Det exakta värdet avrundat till 4 decimaler är \( f\,'(1,8) = 0,5556\, \).
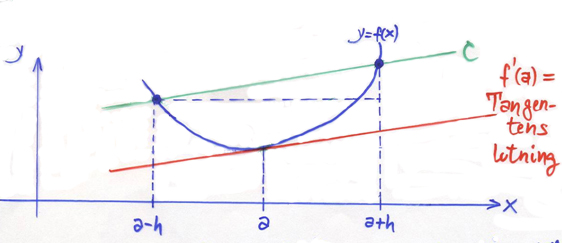
Centrala differenskvoten
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Centrala differenskvoten:
- Tangentens lutning \( \; = \; f\,'(a) \quad \approx \quad {f(a + h) \, - \, f(a-h) \over 2\,h} \; = \; \) Sekanten C:s lutning
Approximationen är desto bättre ju mindre \( h\, \) är.
Exempel 3
Givet:
- Funktionen \( f(x) = x\,^2 \)
- Steglängden \( h = 0,5\, \)
Sökt:
- Funktionens derivata i \( x = 1\, \) dvs \( f\,'(1) \) med centrala differenskvoten .
Lösning:
- \[ f\,'(1) \approx {f(1 + 0,5) - f(1 - 0,5) \over 2\cdot 0,5} = {f(1,5) - f(0,5) \over 2\cdot 0,5} = {1,5^2 - 0,5^2 \over 1} = 2 \]
Funktionens derivata är \( f\,'(x) = 2\,x \) och därmed det exakta värdet \( f\,'(1) = 2 \cdot 1 = 2 \).
Är det en slump att den numeriska deriveringen ger exakt värde, fast steglängden är relativt stor?
Svaret är nej: Den centrala differenskvoten deriverar alla 2:a gradsfunktioner (och förstås även alla 1:a gradsfunktioner) exakt oberoende av steglängden. Här följer beviset:
Sats:
- Den centrala differenskvoten ger den exakta derivatan till alla 2:a gradsfunktioner oberoende av steglängden.
- Om \( f(x) \; = \; x^2 \)
- då \( {f(x + h) \, - \, f(x-h) \over 2\,h} \; = \; 2\,x \)
Bevis\[ {f(x + h) - f(x-h) \over 2\,h} = {(x+h)^2 - (x-h)^2 \over 2\,h} = {(x^2 + 2\,x\,h + h^2) - (x^2 - 2\,x\,h + h^2) \over 2\,h} = \]
\( = {x^2 + 2\,x\,h + h^2 - x^2 + 2\,x\,h - h^2 \over 2\,h} = {4\,x\,h \over 2\,h} = 2\,x = f\,'(x) \)
Det räcker att bevisa satsen för \( f(x) = x^2\, \) som an slags representant för alla 2:a gradsfunktioner, eftersom \( x^2\, \) är den avgörande termen för 2:a gradsfunktioner. Självfallet går det att bevisa satsen även för \( f(x) = a\,x^2 + b\,x + c \). Det tar bara lite längre att räkna. Rsultatet är det samma: Den centrala differenskvoten deriverar 2:a gradsfunktionerna exakt. Att detta är oberoende av steglängden visas i beviset ovan genom att \( h\, \) kan förkortas bort i slutet.
Internetlänkar
http://www.youtube.com/watch?v=OyKmc2bPWe0
http://www.youtube.com/watch?v=8of_svLfcjk
http://www.youtube.com/watch?v=OY8CeLUxE64&feature=related
http://www.youtube.com/watch?v=2wH-g60EJ18&feature=related
http://www.larcentrum.org/Safir/MA1203W/htm/m03_deriv1/m03_deriv_definition.htm
http://www.naturvetenskap.org/index.php?option=com_content&view=article&id=129&Itemid=132
Copyright © 2010-2011 Taifun Alishenas. All Rights Reserved.