Skillnad mellan versioner av "3.3 Terasspunkter"

Från Mathonline
Hoppa till: navigering, sök
m (→‎Hur grafen kan lura oss)
m
 
(483 mellanliggande versioner av samma användare visas inte)
Rad 1: Rad 1:
 +
__NOTOC__
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
−
{{Not selected tab|[[3.2 Lokala maxima och minima|<-- Förra avsnitt]]}}
+
{{Not selected tab|[[3.2 Lokala maxima och minima| <<&nbsp;&nbsp;Förra avsnitt]]}}
−
{{Selected tab|[[3.3 Terasspunkter|Teori]]}}
+
{{Selected tab|[[3.3 Terasspunkter|Genomgång]]}}
 
{{Not selected tab|[[3.3 Övningar till Terasspunkter|Övningar]]}}
 
{{Not selected tab|[[3.3 Övningar till Terasspunkter|Övningar]]}}
−
{{Not selected tab|[[3.4 Kurvkonstruktioner|--> Nästa avsnitt]]}}
+
{{Not selected tab|[[3.4 Kurvkonstruktioner|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
  
  
−
[[Media: Lektion 31 Terasspunkter Ruta.pdf|Lektion 31 Terasspunkter]]
+
<!-- [[Media: Lektion 25 Terasspunkter Ruta.pdf|<b><span style="color:blue">Lektion 25 Terasspunkter</span></b>]] -->
  
−
__TOC__
+
<big>
 +
==== <b><span style="color:#931136">Vad är en terasspunkt?</span></b> ====
 +
<table>
 +
<tr>
 +
  <td>[[Image: Kritiska punkter.jpg]]
  
 +
</td>
 +
  <td>&nbsp;&nbsp;&nbsp;&nbsp;</td>
 +
  <td>
 +
&nbsp;&nbsp;<big>Bilden visar tre punkter där kurvan har tangenter med lutningen <math> \, 0 \, </math>:</big>
  
−
== Terasspunkter ==
 
  
−
I förra avsnitt lärde vi oss två metoder för att hitta en funktions extrempunkter dvs maxima eller minima:
+
* &nbsp;&nbsp; <big>Ett minimum i <math> \, x = -2 \, </math> där gäller<span style="color:black">:</span> <math> \,\, f\,'(-2) \, = \, 0 </math>.</big>
  
−
* Funktionens derivata <math> \, = \, 0 \, </math> och andraderivatan <math> \, < \, 0 \, </math> eller <math> \, > \, 0 \, </math> dvs <math> \, \neq \, 0 \, </math>.
+
* <div class="ovnE">En <b><span style="color:red">terasspunkt</span></b> i <math> \, x = 0 \quad </math> &nbsp;&nbsp;&nbsp; <span style="color:black">:</span> <math> \, f\,'(0) \quad = \, 0 </math>.
 +
</div>
  
−
* Funktionens derivata <math> \, = \, 0 \, </math> och derivatan byter tecken kring sitt nollställe.
+
* &nbsp;&nbsp; <big>Ett maximum i <math> \, x = 2 \, </math> där gäller&nbsp; <span style="color:black">:</span> <math> \,\, f\,'(2) \quad = \, 0 </math>.</big>
 +
  </td>
 +
</tr>
 +
</table>
  
−
Båda metoder utesluter följande alternativ:
 
  
−
* Både funktionens derivata och andraderivata <math> \, = \, 0 \, </math>.
+
Generellt gäller:
  
−
* Funktionens derivata <math> \, = \, 0 \, </math> och derivatan inte byter tecken kring sitt nollställe.
+
==== <b><span style="color:#931136">Regeln om terasspunkt med derivator</span></b> ====
 +
<div class="border-divblue">
 +
<math> f\,'(a) \, = \, f\,''(a) \, = \, 0 \; </math> och <math> \; {\color {Red} {f\,'''(a) \, \neq \, 0}} \quad \Longrightarrow \quad </math> Funktionen <math> \; y = f(x) \; </math> har en <b><span style="color:red">terasspunkt</span></b> i <math> \; x = a \; </math>.
 +
----
 +
Om <math> \, f\,'(a) = f\,''(a) = f\,'''(a) = 0 \, </math> kan endast en korrekt&nbsp; [[3.3_Terasspunkter#Regeln_om_terasspunkt_med_teckenstudie|<b><span style="color:blue">teckenstudie</span></b>]]&nbsp; eller högre derivator avgöra saken.<br>
 +
</div>
  
−
Dessa alternativ tar vi upp nu: Vad händer om funktionens derivata och andraderivata är <math> \, 0 \, </math> eller om derivatan är <math> \, 0 \, </math> och bibehåller sitt tecken kring nollstället?
 
  
−
Ett sådant fall föreligger i följande enkelt exempel:
+
Tredjederivatan är inget annat än andraderivatans derivata. Man får den genom att derivera andraderivatan en gång till enligt deriveringsreglerna.
  
−
::::<math>\begin{array}{rcl}  f(x) & = & x^3    \\
+
==== <b><span style="color:#931136">Kritiska punkter</span></b> ====
−
                            f'(x) & = & 3\,x^2  \\
+
−
                            f''(x) & = & 6\,x
+
−
          \end{array}</math>
+
  
−
Vi ska undersöka funktionen <math> \, f(x) = x^3 \, </math> i och kring punkten <math> \, x = 0 \, </math> genom att titta på följande grafer:
+
<div class="border-divblue">
 +
En punkt <math> \, x = a \, </math> kallas för <b><span style="color:red">kritisk punkt</span></b> om <math> \, f\,'(a) = 0 \, </math>.
 +
----
 +
En kritisk punkt kan vara ett maximum, ett minimum eller en terasspunkt, se grafen ovan.
 +
----
 +
Att vara maximi-, minimi- eller terasspunkt kallas för den kritiska punktens <b><span style="color:red">karaktär</span></b> eller <b><span style="color:red">typ</span></b>.
 +
</div>
  
−
[[Image: Terasspunkt 1.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Terasspunkt 2.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Terasspunkt 3.jpg]]
 
  
−
Funktionens graf till vänster visar att det inte föreligger en extrempunkt i <math> x = 0 </math>, varken ett maximum eller ett minimum. Det handlar snarare om en typ av kritisk punkt som är ny för oss. Kritiskt, därför att <math>-</math> precis som hos extrempunkter <math>-</math> tangenten till kurvan i denna punkt är horisontell dvs har lutningen <math> \, 0 \, </math>. Denna nya typ av kritisk punkt kallas <strong><span style="color:red">terasspunkt</span></strong>.
+
<div class="ovnE"><small>
 +
==== <b><span style="color:#931136">Exempel på terasspunkt med derivator</span></b> ====
 +
Undersök med derivator vilken typ av kritisk punkt funktionen <math> \, f(x) = x\,^3 \, </math> har i punkten <math> \, x = 0 \, </math>.
  
−
Bilden i mitten visar att derivatan har ett nollställe i <math> \, x = 0 \, </math>. Det speciella med detta nollställe är att kurvan inte skär <math> \, x</math>-axeln utan bara berör den. Med andra ord, <math> \, x = 0 \, </math> är en [[1.2_Faktorisering_av_polynom#Dubbelrot|<strong><span style="color:blue">dubbelrot</span></strong>]] till andragradsfunktionen <math> \, f'(x) = 3\,x^2 \, </math>. Detta gör att derivatan inte byter tecken kring <math> \, x = 0 \, </math> utan är positiv både till vänster om och till höger om nollstället. Att derivatan är positiv innebär i sin tur att själva funktionen <math> \, f(x) = x^3 \, </math> är växande både till vänster om och till höger om <math> \, x = 0 \, </math> <math>-</math> ett kännetecken för terasspunkter.
 
  
−
Bilden till höger visar att även andraderivatan har ett nollställe i <math> \, x = 0 \, </math>. Till skillnad från derivatans nollställe är detta nollställe av enkel typ, vilket framgår av att grafen verkligen skär <math> \, x</math>-axeln dvs byter tecken kring <math> \, x = 0 \, </math>. I självaste punkten <math> \, x = 0 \, </math> är andraderivatan varken positiv eller negativ, varav följer att <math> \, x = 0 \, </math> inte är någon extrempunkt för funktionen <math> \, f(x) = x^3 -</math> ytterliare ett kännetecken för terasspunkter.
+
'''Lösning med derivator:'''
  
−
Vi har inte ritat grafen till tredjederivatan <math> \, f'''(x) = 6 </math>, men den är <math> \neq 0 \, </math> vilket <math>-</math> och det är det nya hos terasspunkter <math>-</math> är ett nödvändigt villkor för att funktionen har en terasspunkt i <math> \, x = 0 \, </math>. Därmed lämnar vi vårt enkla exempel och kommer till det allmänna fallet:
+
[[Image: Terasspunkt 1.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Terasspunkt 2.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Terasspunkt 3.jpg]]
  
−
== Regler om terasspunkter ==
+
::<math>\begin{array}{rclclcl}  f(x) & = & x\,^3  &                &    \\
 +
                          f'(x) & = & 3\,x\,^2 & \Longrightarrow & f'(0) = 3\cdot 0^2 = 3\cdot 0 & = & 0  \\
 +
                          f''(x) & = & 6\,x  & \Longrightarrow & f''(0) = 6\cdot 0 & = & 0  \\
 +
                        f'''(x) & = & 6      & \Longrightarrow & f'''(0) = 6  & \neq & 0
 +
        \end{array}</math>
  
−
Tre kriterier behövs för att få reda på en funktions terasspunkt: ett om derivatans nollställen, det andra om andraderivatans nollställen och det tredje om att tredjederivatan inte får vara <math> \, 0 \, </math>. Alla tre måste vara uppfyllda. Generellt gäller:
+
Vi ser att <math> \, f\,'(0) = f\,''(0) = 0 \, </math> och <math> \, f\,'''(0) \neq 0 </math>. Av regeln ovan följer att <math> \, f(x)\, </math> har en <b><span style="color:red">terasspunkt</span></b> i <math> \, x = 0 \, </math> som visas på bilden till vänster.
 +
</small></div>
  
−
<span style="color:white">:</span>
 
−
<div style="border:1px solid black;display:inline-table;margin-left: 15px;padding:10px 20px 10px 20px;-webkit-border-radius: 15px;">
 
−
<big>'''Regeln med högre derivator''':
 
  
 +
'''Bilden i mitten''' visar att derivatan <math> \, f\,'(x) = 3\,x^2 \, </math> endast har ett nollställe i <math> \, x = 0 \, </math> som är en [[1.2_Faktorisering_av_polynom#Dubbelrot|<b><span style="color:blue">dubbelrot</span></b>]]. Dvs kurvan skär inte <math> \, x</math>-axeln, utan ''berör'' den endast. Med andra ord, derivatan byter inte tecken i <math> \, x = 0 \, </math> utan är positiv på båda sidor av <math> \, x = 0 \, </math>. Av detta följer att själva funktionen <math> \, f(x) = x^3 \, </math> är växande på båda sidor av <math> \, x = 0 \, </math> <math>-</math> ett kännetecken för terasspunkter. Generellt gäller:
  
−
Funktionen <math> {\color{White} x} y \, = \, f(x) {\color{White} x} </math> har en <strong><span style="color:red">terasspunkt</span></strong> i <math> {\color{White} x} x = a {\color{White} x} </math> om <math> {\color{White} x} f\,'(a) \, = \, f\,''(a) \, = \, 0 {\color{White} x} </math> och <math> {\color{White} x} f\,'''(a) \, \neq \, 0 {\color{White} x}. </math>
+
<div class="border-divblue">
 +
Funktionen <math> \; y = f(x) \; </math> har en terasspunkt i <math> \; x = a \qquad\;\;\, \Longrightarrow \qquad\quad f\,'(a) \, = \, f\,''(a) \, = \, 0 \; </math>.
 
----
 
----
−
Om <math> {\color{White} x} f\,'(a) \, = \, f\,''(a) \, = \, f\,'''(a) \, = \, 0 {\color{White} x} </math> har funktionen ingen terasspunkt i <math> {\color{White} x} x = a {\color{White} x} </math>.
+
<math> f\,(x) \, </math> är ett tredjegradspolynom som har en terasspunkt <math> \quad \Longrightarrow \quad  f\,'(x) \, </math> är ett andragradspolynom som
  
−
I dett fall kan endast ett teckenstudium avgöra den kritiska punktens typ.
+
endast har <b><span style="color:red">ett</span></b> nollställe, dvs nollstället är en dubbelrot.
−
</big></div>
+
</div>
  
  
−
För att demonstrera regeln ovan tar vi vårt inledande exempel och undersöker regelns tre kriterier algebraiskt i punkten <math> \, x = 0 </math>:
+
Alternativt till användning av derivator finns det alltid möjligheten att genomföra en teckenstudie för att känna igen en terasspunkt:
  
−
::<math>\begin{array}{rclclcl}  f(x) & = & x^3  &                &    \\
 
−
                          f'(x) & = & 3\,x^2 & \Longrightarrow & f'(0) = 3\cdot 0^2 = 3\cdot 0 & = & 0  \\
 
−
                          f''(x) & = & 6\,x  & \Longrightarrow & f''(0) = 6\cdot 0 & = & 0  \\
 
−
                        f'''(x) & = & 6      & \Longrightarrow & f'''(0) = 6  & \neq & 0
 
−
        \end{array}</math>
 
  
−
Vi ser att <math> f'(0) = f''(0) = 0 </math> och <math> f'''(0) \neq 0 </math>. Enligt regeln ovan drar vi slutsatsen att funktionen <math> f(x)\, </math> har en <strong><span style="color:red">terasspunkt</span></strong> i <math> \, x = 0 </math>.
+
==== <b><span style="color:#931136">Regeln om terasspunkt med teckenstudie</span></b> ====
 +
<div class="border-divblue">
 +
<math> f\,'(a) = 0 \; </math> och <math> \; f\,'(x) </math> <b><span style="color:red">inte byter tecken</span></b> i <math> \, x=a \quad \Longrightarrow \quad </math> Funktionen <math> \; y = f(x) \; </math> har en <b><span style="color:red">terasspunkt</span></b> i <math> \; x = a \; </math>.
 +
<br>
 +
</div>
  
−
Alternativt till användning av högre derivator finns det alltid möjligheten att genomföra ett teckenstudium för att känna igen en terasspunkt.
+
Med andra ord, i en terasspunkt <math> \, x=a </math> måste derivatan vara <math> \, 0 </math>, utan att byta tecken i <math> \, a </math>, dvs derivatan är antingen positiv eller negativ på <i>båda</i> sidor av <math> \, x=a </math>.  
  
−
Här finns det två kriterier för att få reda på en funktions terasspunkt: ett om derivatans nollställen och ett om att derivatan inte byter tecken:
 
  
−
<span style="color:white">:</span>
+
<div class="ovnE"><small>
−
<div style="border:1px solid black;display:inline-table;margin-left: 15px;padding:10px 20px 10px 20px;-webkit-border-radius: 15px;">
+
==== <b><span style="color:#931136">Exempel på terasspunkt med teckenstudie</span></b> ====
−
<big>'''Regeln med teckenstudium''':
+
Undersök med en teckenstudie vilken typ av kritisk punkt funktionen <math> \, f(x) = x\,^3 \, </math> har i punkten <math> \, x = 0 \, </math>.
  
 +
'''Lösning med teckenstudie:'''
 +
<table>
 +
<tr>
 +
  <td>Vi hade redan bestämt att
  
−
Funktionen <math> {\color{White} x} y \, = \, f(x) {\color{White} x} </math> har en <strong><span style="color:red">terasspunkt</span></strong> i <math> {\color{White} x} x = a {\color{White} x} </math> om <math> {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} </math> och <math> {\color{White} x} f\,'(x) {\color{White} x} </math> inte byter tecken kring <math> \, a </math>.
+
derivatan var <math> \, 0 </math> för <math> \, x = 0 \, </math>:
−
</big></div>
+
  
  
−
Att derivatan inte byter tecken innebär för att den antingen är positiv eller negativ på <i>båda</i> sidor av sitt nollställe.
 
−
 
−
För att demonstrera regeln med teckenstudium tar vi samma exempel <math> \, f(x) = x^3 \, </math>. Vi hade redan bestämt att derivatan var <math> \, 0 </math> för <math> \, x = 0 \, </math>:
 
  
 +
</td>
 +
  <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;</td>
 +
  <td>
 
::<math> f(x) = x^3 </math>
 
::<math> f(x) = x^3 </math>
  
Rad 98: Rad 121:
  
 
::<math> f'(0) = 3\cdot 0^2 = 3\cdot 0 = 0 </math>
 
::<math> f'(0) = 3\cdot 0^2 = 3\cdot 0 = 0 </math>
 +
</td>
 +
</tr>
 +
</table>
 +
Nu ska vi undersöka derivatans tecken till vänster och till höger om nollstället <math> \, x = 0 </math>.
  
−
Nu ska vi undersöka derivatans tecken till vänster och till höger om nollstället <math> \, x = 0 </math>. Vi väljer t.ex. punkterna <math> \, x = -0,1 </math> och <math> \, x = 0,1 </math> på <math> \, x</math>-axeln som är ganska nära derivatans nollställe och bestämmer derivatans tecken i dessa punkter:
+
Vi väljer t.ex. punkterna <math> \, x = -0,1 </math> och <math> \, x = 0,1 </math> och bestämmer derivatans tecken i dessa punkter:
  
 +
<table>
 +
<tr>
 +
  <td>
 
::<math> f' (-0,1) = 3\cdot (-0,1)^2 = 3\cdot 0,01 = 0,03 > 0 </math>
 
::<math> f' (-0,1) = 3\cdot (-0,1)^2 = 3\cdot 0,01 = 0,03 > 0 </math>
  
 
::<math> f' (0,1) = 3\cdot (0,1)^2 = 3\cdot 0,01 = 0,03 > 0 </math>
 
::<math> f' (0,1) = 3\cdot (0,1)^2 = 3\cdot 0,01 = 0,03 > 0 </math>
−
 
+
</td>
−
Resultaten överförs till följande teckentabell:
+
  <td>                <table RULES="ALL" class="spaced-table" style="margin-left:50px;">
−
 
+
−
                <table RULES="ALL" class="spaced-table" style="margin-left:30px;">
+
 
   <tr>
 
   <tr>
 
     <td><math>x</math></td>
 
     <td><math>x</math></td>
Rad 122: Rad 150:
 
   <tr>
 
   <tr>
 
     <td><math> \,f(x) </math></td>
 
     <td><math> \,f(x) </math></td>
−
     <td> <strong><big><big>&#8599;</big></big></strong> </td>
+
     <td> <b><big><big>&#8599;</big></big></b> </td>
−
     <td> <strong><span style="color:red">Terass</span></strong> </td>
+
     <td> <b><span style="color:red">Terass</span></b> </td>
−
     <td> <strong><big><big>&#8599;</big></big></strong> </td>
+
     <td> <b><big><big>&#8599;</big></big></b> </td>
 
   </tr>
 
   </tr>
 
</table>
 
</table>
 +
</td>
 +
</tr>
 +
</table>
 +
Dessa resultat är infogade i teckentabellen till höger som visar:
 +
 +
# <math> \, f\,'(0) = 0 \, </math>
 +
# Derivatan har tecknet <math>+</math> till vänster och även <math> + </math> till höger om <math> \, 0 \, </math> dvs derivatan byter inte tecken kring sitt nollställe.
 +
 +
Enligt regeln om terasspunkt med teckenstudie drar vi slutsatsen att funktionen <math> f(x)\, </math> har en <b><span style="color:red">terasspunkt</span></b> i <math> \, x = 0 </math>.
 +
</small></div>
  
−
Vi ser att <math> f\,'(0) = 0 </math> och derivatan har tecknet <math>+</math> till vänster om och <math> + </math> till höger om <math> \, 0 </math> dvs är positiv och inte byter tecken kring sitt nollställe. Enligt regeln med teckenstudium drar vi slutsatsen att funktionen <math> f(x)\, </math> har en <strong><span style="color:red">terasspunkt</span></strong> i <math> \, x = 0 </math>.
 
  
 +
Avgörande för att teckenstudie är en korrekt algebraisk metod är förutsättningen att <math> \; y \, = \, f(x) \; </math> är [[1.5_Kontinuerliga_och_diskreta_funktioner|<b><span style="color:blue">kontinuerlig</span></b>]] i alla punkter av det betraktade området.
  
−
== Hur grafen kan lura oss ==
 
  
 +
<div class="forsmak">
 +
==== <b><span style="color:#931136">Hur grafen kan lura oss</span></b> ====
 
<table>
 
<table>
 
<tr>
 
<tr>
−
   <td>Vi modifierar det inledande exemplet lite grann
+
   <td>[[Image: Hur grafen kan lura oss.jpg]]</td>
 +
  <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;</td>
 +
  <td>Har funktionen
  
−
genom att lägga till en term till funktionsuttrycket:
+
:::::<math> f(x) = x^3 + \, 0,5\,x </math>
  
−
::::<math> f(x) = x^3 + \, 0,5\,x </math>
+
vars graf visas till vänster en terasspunkt i <math> \, x = 0 \, </math>?
  
−
Bilden till höger visar grafen till den här funktionen.
+
Kurvan är av samma typ som <math> g(x) = x^3 </math> till höger.
  
−
Kan man från grafen dra slutsatsen att <math> f(x) </math> har en
+
Ritar man båda funktioners grafer i miniräknarens
  
−
terasspunkt i <math> \, x  = 0 \, </math>? Kurvan verkar vara av samma
+
display är det svårt att se skillnaden. Slutsatsen att
  
−
typ som det inledande exemplet <math> y = \, x^3 \, </math>. Speciellt
+
även <math> f(x) </math> har en terasspunkt i <math> x  = 0 </math> ligger nära.
  
−
om grafen ritas på en miniräknares lilla display ser
+
Men <math> f\,'(0) \neq 0 </math> visar att detta inte är fallet:
−
 
+
   <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;</td>
−
man kanske t.o.m. ingen skillnad alls till kurvan
+
  <td>[[Image: Hur grafen kan lura oss 2.jpg]]</td>
−
 
+
−
<math> y = \, x^3 \, </math>. Den spontana slutsatsen att det här också
+
−
 
+
−
</td>
+
−
   <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image: Hur grafen kan lura oss.jpg]]</td>
+
 
</tr>
 
</tr>
 
</table>
 
</table>
−
är en terasspunkt är i alla fall inte ovanligt. En liten tvekan kommer upp när man jämför de olika funktionsuttrycken. Men hur kan man få 100 %-ig klarhet om detta?
 
−
 
−
Det enda sättet att göra det är att tillämpa de algebraiska regler som vi ställde upp inledningsvis <math>-</math> antingen regeln med högre derivator eller regeln med teckenstudium. Båda kräver bl.a. att derivatan blir <math> \, 0 \, </math> i <math> \, x  = 0 \, </math>. Men det visar sig att detta inte är fallet:
 
−
 
 
:::<math>\begin{array}{rcl}  f(x) & = & x^3 + \, 0,5\,x  \\
 
:::<math>\begin{array}{rcl}  f(x) & = & x^3 + \, 0,5\,x  \\
 
                             f'(x) & = & 3\,x^2 + \, 0,5  \\
 
                             f'(x) & = & 3\,x^2 + \, 0,5  \\
Rad 168: Rad 200:
 
         \end{array}</math>
 
         \end{array}</math>
  
−
Därmed är frågan avgjord<span style="color:black">:</span> <math> f(x) </math> har ingen terasspunkt i <math> \, x  = 0 \, </math>. Grafen har lurat oss.
+
Dvs redan första kravet i [[3.3_Terasspunkter#Regeln_om_terasspunkt_med_derivator|<b><span style="color:blue">regeln om terasspunkt med derivator</span></b>]], nämligen att derivatan ska vara <math> \, 0 \, </math> för <math> \, x  = 0 \, </math> är inte uppfyllt<span style="color:black">:</span> <math> \, f(x) \, </math> har ingen terasspunkt i <math> \, x  = 0 \, </math>. Grafen har lurat oss.
 +
</div> <!-- forsmak -->
 +
 
 +
 
 +
Vill man använda grafer borde man först undersöka funktionen med de strikta algebraiska reglerna och sedan rita grafer för att visualisera resultatet. I det här fallet är det lämpligt att även rita tangenten till <math> \, f(x) \, </math> i <math> \, x = 0 \, </math>. Lägger man till graferna till derivatan och andraderivatan får man en fullständig överblick över funktionens beteende i och kring <math> \, x = 0 \, </math>:
  
−
Vill man använda grafer borde man först undersöka funktionen med de strikta algebraiska reglerna och sedan rita grafer för att visualisera resultatet. I det här fallet är det lämpligt att även rita tangenten till <math> \, f(x) \, </math> i <math> \, x = 0 \, </math>. Grafer till derivatan och andraderivatan ger en fullständig överblick över funktionens beteende:
 
  
 
[[Image: Inflexionspunkt 1a.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Inflexionspunkt 2a.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Inflexionspunkt 3a.jpg]]
 
[[Image: Inflexionspunkt 1a.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Inflexionspunkt 2a.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Inflexionspunkt 3a.jpg]]
  
  
−
+++
+
'''Bilden till vänster''' visar funktionens graf samt tangenten till kurvan i <math> \, x = 0 </math>. Tangenten är inte horisontell dvs har inte lutningen <math> \, 0 </math>. I beräkningen ovan hade vi fått<span style="color:black">:</span> <math> f'(x) = 0,5 \neq 0 </math>. Därmed är även tangentens lutning <math> \, 0,5 \, </math> och dess ekvation<span style="color:black">:</span> <math> y = 0,5\,x </math>. Därför föreligger i <math> \, x = 0 \, </math> inte en terasspunkt.
 +
 
 +
'''Bilden i mitten''' visar att derivatan inte har något nollställe vilket visar att funktionen varken har extrempunkter eller terasspunkter. Derivatan är alltid positiv och antar i <math> x = 0 </math> värdet <math> \, 0,5 \, </math>. Om detta värde hade varit <math> \, 0 \, </math> hade funktionen haft en terasspunkt i <math> x = 0 </math>.
 +
 
 +
'''Bilden till höger''' visar att andraderivatan har ett nollställe i <math> \, x = 0 \, </math>, där grafen skär <math> \, x</math>-axeln. Vad innebär detta? Vi har inte haft ett sådant fall där derivatan är skild från <math> \, 0 \, </math>, men andraderivatan är <math> \, 0 \, </math>. Därför handlar det om en speciell punkt på kurvan som varken är extrem- eller terasspunkt, för i dessa fall borde ju derivatan vara <math> \, 0 \, </math>. Faktiskt handlar det om en ny typ av punkt som kallas <b><span style="color:red">inflexionspunkt</span></b>.
 +
 
 +
=== <b><span style="color:#931136">Inflexionspunkter</span></b> ===
 +
<div class="ovnC"><small>
 +
<table>
 +
<tr>
 +
  <td>[[Image: Inflexionspunkt 4.jpg]]</td>
 +
  <td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;</td>
 +
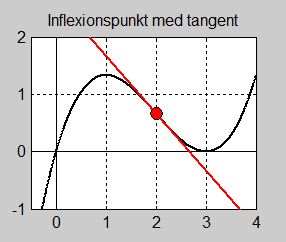
  <td>Om du föreställer dig att du kör bil på S-kurvan på bilden till vänster,
 +
 
 +
svänger du ratten först till höger tills du kommer till S-kurvans mitt<span style="color:black">:</span>
 +
     
 +
<math> \, x = 2 \, </math>. Sedan byter du svängriktning och rattar till vänster.
 +
 
 +
Punkten i <math> \, x = 2 \, </math> där du byter svängriktning kallas för <b><span style="color:red">inflexionspunkt</span></b>.
 +
 
 +
Inflexionspunkter är sådana där kurvan går över från en högersväng
 +
 
 +
(''konkav'' kurva) till en vänstersväng (''konvex'' kurva) eller tvärtom <math>-</math>
 +
 
 +
allt sett från vänster och underifrån.
 +
 
 +
På bilden finns även tangenten ritad i <math> \, x = 2 \, </math> vars lutning är negativ.
 +
 
 +
Hade lutningen varit <math> \, 0 \, </math> hade <math> \, x = 2 \, </math> varit en terasspunkt. Därför:
 +
  </td>
 +
</tr>
 +
</table>
 +
Terasspunkter är specialfall av inflexionspunkter, eftersom kurvan byter alltid svängriktning i en terasspunkt.
 +
 
 +
Men inte alla inflexionspunkter är terasspunkter. Inflexionspunkter kan ha tangenter med vilken lutning som helst.
 +
 
 +
Terasspunkter är sådana inflexionspunkter där tangenten har lutningen <math> \, 0 \, </math>.
 +
 
 +
Pga funktionens kontinuitet finns alltid en inflexionspunkt mellan två extrempunkter.
 +
</small></div>
 +
 
 +
==== <b><span style="color:#931136">Regeln om inflexionspunkter</span></b> ====
 +
<div class="border-divblue">
 +
<math> f\,''(a) \, = \, 0 \; </math> och <math> \; f\,'''(a) \, \neq \, 0 \; \quad \Longrightarrow \quad </math> Funktionen <math> \; y \, = \, f(x) \; </math> har en <b><span style="color:red">inflexionspunkt</span></b> i <math> \; x = a \; </math>.
 +
----
 +
Om dessutom <math> \; f\,'(a) \, = \, 0 \; </math> är <math> \; x = a \; </math> en terasspunkt. &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (Samma som [[3.3_Terasspunkter#Regeln_om_terasspunkt_med_derivator|<b><span style="color:blue">tidigare</span></b>]])
 +
----
 +
En terasspunkt är alltid en inflexionspunkt, men inte tvärtom.
 +
</div>
 +
 
 +
För att hitta inflexionspunkter ställer man alltså upp andraderivatan, sätter den till <math> \, 0 \, </math> och beräknar<math> \, x </math>, dvs andraderivatans nollställen. Sedan kontrollerar man om tredjederivatan verkligen är skild från <math> \, 0 \, </math> för andraderivatans nollställen.
 +
 
 +
I inflexionspunkter går funktionens graf över från en konkav kurva till en konvex kurva eller tvärtom. När är en funktion konvex eller konkav?
 +
 
 +
 
 +
 
 +
=== <b><span style="color:#931136">Konvexa och konkava funktioner</span></b> ===
 +
<div class="border-divblue">
 +
<math> f\,''(x) > 0 \, </math> i ett visst intervall <math> \; \quad \Longrightarrow \quad </math> Funktionen <math> \, y = f(x) \, </math> är <b><span style="color:red">konvex</span></b> i intervallet.
 +
 
 +
T.ex. är kurvan konvex till höger om inflexionspunkten <math> \, x = 2 \, </math> i grafen ovan.
 +
----
 +
<math> f\,''(x) < 0 \, </math> i ett visst intervall <math> \; \quad \Longrightarrow \quad </math> Funktionen <math> \, y = f(x) \, </math> är <b><span style="color:red">konkav</span></b> i intervallet.
 +
 
 +
T.ex. är kurvan konkav till vänster om inflexionspunkten <math> \, x = 2 \, </math> i grafen ovan.
 +
----
 +
Allt sett från vänster och underifrån, dvs i axlarnas växande riktning.
 +
</div>
 +
</big>
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
[[Matte:Copyrights|Copyright]] © 2011-2019 Taifun Alishenas. All Rights Reserved.

Nuvarande version från 28 februari 2019 kl. 15.41

        <<  Förra avsnitt          Genomgång          Övningar          Nästa avsnitt  >>      


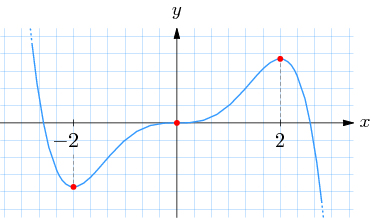
Vad är en terasspunkt?

Kritiska punkter.jpg     

  Bilden visar tre punkter där kurvan har tangenter med lutningen \( \, 0 \, \):


  •    Ett minimum i \( \, x = -2 \, \) där gäller: \( \,\, f\,'(-2) \, = \, 0 \).
  • En terasspunkt i \( \, x = 0 \quad \)     : \( \, f\,'(0) \quad = \, 0 \).
  •    Ett maximum i \( \, x = 2 \, \) där gäller  : \( \,\, f\,'(2) \quad = \, 0 \).


Generellt gäller:

Regeln om terasspunkt med derivator

\( f\,'(a) \, = \, f\,''(a) \, = \, 0 \; \) och \( \; {\color {Red} {f\,'''(a) \, \neq \, 0}} \quad \Longrightarrow \quad \) Funktionen \( \; y = f(x) \; \) har en terasspunkt i \( \; x = a \; \).

Om \( \, f\,'(a) = f\,''(a) = f\,'''(a) = 0 \, \) kan endast en korrekt  teckenstudie  eller högre derivator avgöra saken.


Tredjederivatan är inget annat än andraderivatans derivata. Man får den genom att derivera andraderivatan en gång till enligt deriveringsreglerna.

Kritiska punkter

En punkt \( \, x = a \, \) kallas för kritisk punkt om \( \, f\,'(a) = 0 \, \).

En kritisk punkt kan vara ett maximum, ett minimum eller en terasspunkt, se grafen ovan.

Att vara maximi-, minimi- eller terasspunkt kallas för den kritiska punktens karaktär eller typ.


Exempel på terasspunkt med derivator

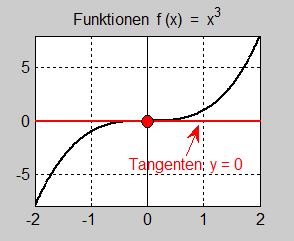
Undersök med derivator vilken typ av kritisk punkt funktionen \( \, f(x) = x\,^3 \, \) har i punkten \( \, x = 0 \, \).


Lösning med derivator:

Terasspunkt 1.jpg      Terasspunkt 2.jpg      Terasspunkt 3.jpg

\[\begin{array}{rclclcl} f(x) & = & x\,^3 & & \\ f'(x) & = & 3\,x\,^2 & \Longrightarrow & f'(0) = 3\cdot 0^2 = 3\cdot 0 & = & 0 \\ f''(x) & = & 6\,x & \Longrightarrow & f''(0) = 6\cdot 0 & = & 0 \\ f'''(x) & = & 6 & \Longrightarrow & f'''(0) = 6 & \neq & 0 \end{array}\]

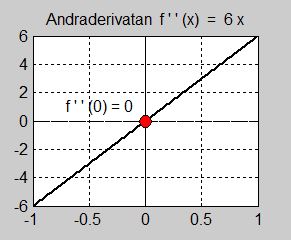
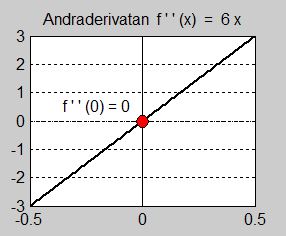
Vi ser att \( \, f\,'(0) = f\,''(0) = 0 \, \) och \( \, f\,'''(0) \neq 0 \). Av regeln ovan följer att \( \, f(x)\, \) har en terasspunkt i \( \, x = 0 \, \) som visas på bilden till vänster.


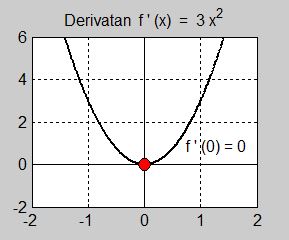
Bilden i mitten visar att derivatan \( \, f\,'(x) = 3\,x^2 \, \) endast har ett nollställe i \( \, x = 0 \, \) som är en dubbelrot. Dvs kurvan skär inte \( \, x\)-axeln, utan berör den endast. Med andra ord, derivatan byter inte tecken i \( \, x = 0 \, \) utan är positiv på båda sidor av \( \, x = 0 \, \). Av detta följer att själva funktionen \( \, f(x) = x^3 \, \) är växande på båda sidor av \( \, x = 0 \, \) \(-\) ett kännetecken för terasspunkter. Generellt gäller:

Funktionen \( \; y = f(x) \; \) har en terasspunkt i \( \; x = a \qquad\;\;\, \Longrightarrow \qquad\quad f\,'(a) \, = \, f\,''(a) \, = \, 0 \; \).

\( f\,(x) \, \) är ett tredjegradspolynom som har en terasspunkt \( \quad \Longrightarrow \quad f\,'(x) \, \) är ett andragradspolynom som

endast har ett nollställe, dvs nollstället är en dubbelrot.


Alternativt till användning av derivator finns det alltid möjligheten att genomföra en teckenstudie för att känna igen en terasspunkt:


Regeln om terasspunkt med teckenstudie

\( f\,'(a) = 0 \; \) och \( \; f\,'(x) \) inte byter tecken i \( \, x=a \quad \Longrightarrow \quad \) Funktionen \( \; y = f(x) \; \) har en terasspunkt i \( \; x = a \; \).

Med andra ord, i en terasspunkt \( \, x=a \) måste derivatan vara \( \, 0 \), utan att byta tecken i \( \, a \), dvs derivatan är antingen positiv eller negativ på båda sidor av \( \, x=a \).


Exempel på terasspunkt med teckenstudie

Undersök med en teckenstudie vilken typ av kritisk punkt funktionen \( \, f(x) = x\,^3 \, \) har i punkten \( \, x = 0 \, \).

Lösning med teckenstudie:

Vi hade redan bestämt att

derivatan var \( \, 0 \) för \( \, x = 0 \, \):


     
\[ f(x) = x^3 \]
\[ f'(x) = 3\,x^2 \]
\[ f'(0) = 3\cdot 0^2 = 3\cdot 0 = 0 \]

Nu ska vi undersöka derivatans tecken till vänster och till höger om nollstället \( \, x = 0 \).

Vi väljer t.ex. punkterna \( \, x = -0,1 \) och \( \, x = 0,1 \) och bestämmer derivatans tecken i dessa punkter:

\[ f' (-0,1) = 3\cdot (-0,1)^2 = 3\cdot 0,01 = 0,03 > 0 \]
\[ f' (0,1) = 3\cdot (0,1)^2 = 3\cdot 0,01 = 0,03 > 0 \]
\(x\) \(-0,1\) \(0\) \(0,1\)
\( f\,'(x) \) \(+\) \(0\) \(+\)
\( \,f(x) \) ↗ Terass ↗

Dessa resultat är infogade i teckentabellen till höger som visar:

  1. \( \, f\,'(0) = 0 \, \)
  2. Derivatan har tecknet \(+\) till vänster och även \( + \) till höger om \( \, 0 \, \) dvs derivatan byter inte tecken kring sitt nollställe.

Enligt regeln om terasspunkt med teckenstudie drar vi slutsatsen att funktionen \( f(x)\, \) har en terasspunkt i \( \, x = 0 \).


Avgörande för att teckenstudie är en korrekt algebraisk metod är förutsättningen att \( \; y \, = \, f(x) \; \) är kontinuerlig i alla punkter av det betraktade området.


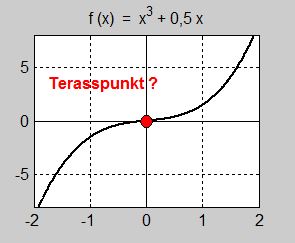
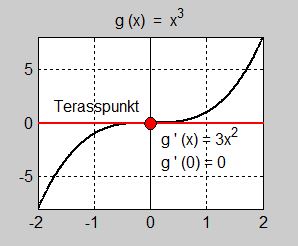
Hur grafen kan lura oss

Hur grafen kan lura oss.jpg        Har funktionen
\[ f(x) = x^3 + \, 0,5\,x \]

vars graf visas till vänster en terasspunkt i \( \, x = 0 \, \)?

Kurvan är av samma typ som \( g(x) = x^3 \) till höger.

Ritar man båda funktioners grafer i miniräknarens

display är det svårt att se skillnaden. Slutsatsen att

även \( f(x) \) har en terasspunkt i \( x = 0 \) ligger nära.

Men \( f\,'(0) \neq 0 \) visar att detta inte är fallet:

       Hur grafen kan lura oss 2.jpg
\[\begin{array}{rcl} f(x) & = & x^3 + \, 0,5\,x \\ f'(x) & = & 3\,x^2 + \, 0,5 \\ f'(0) & = & 3\cdot 0^2 + \, 0,5 = 3\cdot 0 \, + \, 0,5 = 0 \, + \, 0,5 \, = \, 0,5 \, \neq \, 0 \end{array}\]

Dvs redan första kravet i regeln om terasspunkt med derivator, nämligen att derivatan ska vara \( \, 0 \, \) för \( \, x = 0 \, \) är inte uppfyllt: \( \, f(x) \, \) har ingen terasspunkt i \( \, x = 0 \, \). Grafen har lurat oss.


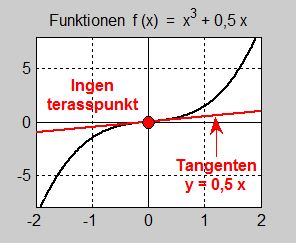
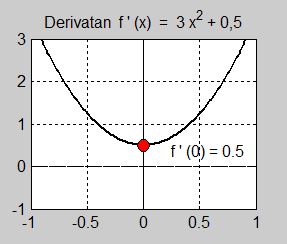
Vill man använda grafer borde man först undersöka funktionen med de strikta algebraiska reglerna och sedan rita grafer för att visualisera resultatet. I det här fallet är det lämpligt att även rita tangenten till \( \, f(x) \, \) i \( \, x = 0 \, \). Lägger man till graferna till derivatan och andraderivatan får man en fullständig överblick över funktionens beteende i och kring \( \, x = 0 \, \):


Inflexionspunkt 1a.jpg      Inflexionspunkt 2a.jpg      Inflexionspunkt 3a.jpg


Bilden till vänster visar funktionens graf samt tangenten till kurvan i \( \, x = 0 \). Tangenten är inte horisontell dvs har inte lutningen \( \, 0 \). I beräkningen ovan hade vi fått: \( f'(x) = 0,5 \neq 0 \). Därmed är även tangentens lutning \( \, 0,5 \, \) och dess ekvation: \( y = 0,5\,x \). Därför föreligger i \( \, x = 0 \, \) inte en terasspunkt.

Bilden i mitten visar att derivatan inte har något nollställe vilket visar att funktionen varken har extrempunkter eller terasspunkter. Derivatan är alltid positiv och antar i \( x = 0 \) värdet \( \, 0,5 \, \). Om detta värde hade varit \( \, 0 \, \) hade funktionen haft en terasspunkt i \( x = 0 \).

Bilden till höger visar att andraderivatan har ett nollställe i \( \, x = 0 \, \), där grafen skär \( \, x\)-axeln. Vad innebär detta? Vi har inte haft ett sådant fall där derivatan är skild från \( \, 0 \, \), men andraderivatan är \( \, 0 \, \). Därför handlar det om en speciell punkt på kurvan som varken är extrem- eller terasspunkt, för i dessa fall borde ju derivatan vara \( \, 0 \, \). Faktiskt handlar det om en ny typ av punkt som kallas inflexionspunkt.

Inflexionspunkter

Inflexionspunkt 4.jpg       Om du föreställer dig att du kör bil på S-kurvan på bilden till vänster,

svänger du ratten först till höger tills du kommer till S-kurvans mitt:

\( \, x = 2 \, \). Sedan byter du svängriktning och rattar till vänster.

Punkten i \( \, x = 2 \, \) där du byter svängriktning kallas för inflexionspunkt.

Inflexionspunkter är sådana där kurvan går över från en högersväng

(konkav kurva) till en vänstersväng (konvex kurva) eller tvärtom \(-\)

allt sett från vänster och underifrån.

På bilden finns även tangenten ritad i \( \, x = 2 \, \) vars lutning är negativ.

Hade lutningen varit \( \, 0 \, \) hade \( \, x = 2 \, \) varit en terasspunkt. Därför:

Terasspunkter är specialfall av inflexionspunkter, eftersom kurvan byter alltid svängriktning i en terasspunkt.

Men inte alla inflexionspunkter är terasspunkter. Inflexionspunkter kan ha tangenter med vilken lutning som helst.

Terasspunkter är sådana inflexionspunkter där tangenten har lutningen \( \, 0 \, \).

Pga funktionens kontinuitet finns alltid en inflexionspunkt mellan två extrempunkter.

Regeln om inflexionspunkter

\( f\,''(a) \, = \, 0 \; \) och \( \; f\,'''(a) \, \neq \, 0 \; \quad \Longrightarrow \quad \) Funktionen \( \; y \, = \, f(x) \; \) har en inflexionspunkt i \( \; x = a \; \).

Om dessutom \( \; f\,'(a) \, = \, 0 \; \) är \( \; x = a \; \) en terasspunkt.            (Samma som tidigare)

En terasspunkt är alltid en inflexionspunkt, men inte tvärtom.

För att hitta inflexionspunkter ställer man alltså upp andraderivatan, sätter den till \( \, 0 \, \) och beräknar\( \, x \), dvs andraderivatans nollställen. Sedan kontrollerar man om tredjederivatan verkligen är skild från \( \, 0 \, \) för andraderivatans nollställen.

I inflexionspunkter går funktionens graf över från en konkav kurva till en konvex kurva eller tvärtom. När är en funktion konvex eller konkav?


Konvexa och konkava funktioner

\( f\,''(x) > 0 \, \) i ett visst intervall \( \; \quad \Longrightarrow \quad \) Funktionen \( \, y = f(x) \, \) är konvex i intervallet.

T.ex. är kurvan konvex till höger om inflexionspunkten \( \, x = 2 \, \) i grafen ovan.

\( f\,''(x) < 0 \, \) i ett visst intervall \( \; \quad \Longrightarrow \quad \) Funktionen \( \, y = f(x) \, \) är konkav i intervallet.

T.ex. är kurvan konkav till vänster om inflexionspunkten \( \, x = 2 \, \) i grafen ovan.

Allt sett från vänster och underifrån, dvs i axlarnas växande riktning.





Copyright © 2011-2019 Taifun Alishenas. All Rights Reserved.

Hämtad från "https://matte3c.mathonline.se/index.php?title=3.3_Terasspunkter&oldid=36534"