Skillnad mellan versioner av "1.2 Faktorisering av polynom"

Från Mathonline
Hoppa till: navigering, sök
m (→‎Faktorisering av 3:e och högre gradspolynom)
m
 
(566 mellanliggande versioner av samma användare visas inte)
Rad 1: Rad 1:
 +
__NOTOC__
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
−
{{Selected tab|[[1.3 Faktorisering av polynom|Teori]]}}
+
{{Not selected tab|[[1.1 Polynom| <<&nbsp;&nbsp;Förra avsnitt]]}}
−
{{Not selected tab|[[1.3 Övningar till Faktorisering av polynom|Övningar]]}}
+
{{Selected tab|[[1.2 Faktorisering av polynom|Genomgång]]}}
 +
{{Not selected tab|[[1.2 Övningar till Faktorisering av polynom|Övningar]]}}
 +
{{Not selected tab|[[1.2 Fördjupning till Faktorisering av Polynom|Fördjupning]]}}
 +
{{Not selected tab|[[1.3 Rationella uttryck|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
  
  
−
== Vad är en faktor? ==
+
<!-- [[Media: Lektion_4_Faktorisering_av_polynom_Rutaa.pdf|<b><span style="color:blue">Lektion 4 Faktorisering av polynom</span></b>]]
  
−
Du minns väl att ett uttryck av formen
+
[[Media: Lektion_5_Faktorisering_av_polynom_Ruta.pdf|<b><span style="color:blue">Lektion 5 Faktorisering av polynom: Fördjupning</span></b>]]
 +
-->
 +
== <b><span style="color:#931136">Faktorisering av tal</span></b> ==
 +
<big>Matte 1:</big>
 +
<div class="ovnE">
 +
<math> a \cdot b \quad </math> är en produkt, där <math>a\,</math> och <math>b\,</math> kallas för <b><span style="color:red">faktorer</span></b>.
  
−
:::::::::::::::<math> a \cdot b </math>
+
Därför är t.ex. <math> \quad \boxed{12 \, = \, 3 \cdot 4} \quad </math> en <b><span style="color:red">faktorisering</span></b> av
  
−
är en <span style="color:red">produkt</span>. Ingredienserna <math>a</math> och <math>b</math> kallas <span style="color:red">faktorer</span>. Så länge <math>a</math> och <math>b</math> står som variabler (platshållare) för tal är uttrycket ovan en faktorform för tal. T.ex. är produkten
+
talet <math> \, 12 \, </math> och <math> \, 3 \cdot 4 \, </math> kallas för en <b><span style="color:red">faktorform</span></b> av talet.
  
−
:::::::::::::::<math> 3 \cdot 4 </math>
+
En annan faktorform är <math> \, 3 \cdot 2\cdot 2 \, </math> (Primfaktorer).
 +
</div>
  
−
en faktorform för talet 12. Processen att ta fram denna faktorform dvs produkten 3 <math>\cdot</math> 4 kallas <span style="color:red">faktorisering</span> av 12. Analog till faktorisering av heltal kan även polynom faktoriseras.
 
  
−
En faktorisering av polynom innebär att skriva om polynomet, som ursprungligen är en summa av termer, till en produkt. T.ex.: 
+
<big>
 +
<b><span style="color:red">Faktorisering</span></b> betyder alltså omvandling till en produkt.
  
−
::::::::::<math> x^2 - 7\,x + 12 = (x-3) \cdot (x-4) </math>
+
Analogt till faktorisering av heltal kan även ett polynom som ursprungligen är en summa av termer, faktoriseras dvs skrivas om till en produkt.
 +
</big>
  
−
Till vänster om likhetstecknet har vi polynomet som en summa av termer. Till höger står samma polynom som en produkt av faktorer. Den nya formen kallas <span style="color:red">polynom i faktorform</span> och är resultat av faktorisering. Ingredienserna i faktorformen dvs faktorerna <math> (x-3)\, </math> och <math> (x-4)\, </math> är i sin tur polynom, fast av mindre grad, nämligen 1. Ursprungspolynomet är av grad 2, liknande faktorerna 3 och 4 som är mindre än 12. Man har splittrat upp det hela i sina beståndsdelar: talet 12 i sina beståndsdelar 3 och 4 och polynomet <math> x^2 - 7\,x + 12 </math> i sina beståndsdelar <math> (x-3)\, </math> och <math> (x-4)\, </math>.
 
  
−
Matematiskt inser man likheten ovan genom att utveckla högerledet dvs produkten:  
+
== <b><span style="color:#931136">Enkel faktorisering av polynom</span></b> ==
 +
<big>Matte 2:</big>
 +
<div class="ovnC">
 +
[[1.3_Rationella_uttryck#Repetition:_Kvadreringsreglerna_och_konjugatregeln|<b><span style="color:blue">Kvadreringsregeln</span></b>]] <math> \, (a-b)\,^2 = a^2 - 2\,a\,b + b^2 \, </math> ger t.ex.<span style="color:black">:</span>
  
−
:::::::<math> (x-3) \cdot (x-4) = x^2 - 4\,x - 3\,x + 3 \cdot 4 = x^2 - 7\,x + 12 </math>
+
<math> \qquad\qquad\qquad\quad\;\; (x-3)\,^2 \; = \; x^2 - 2 \cdot x \cdot 3 + 3^2 \; = \; x^2 - 6\,x + 9 </math>
  
−
Men hur får man fram faktorformen från polynomet? Dvs hur faktoriserar man ett polynom? Frågan är relevant, för det första därför att faktorformen tillåter förkortning och därmed förenkling av komplexa algebraiska uttryck och för det andra därför att den avslöjar polynomets nollställen. Vi kommer att förstå detta bättre i fortsättningen.
+
Läser vi baklänges får vi en faktorisering av polynomet <math> \, x^2 - 6\,x + 9 \, </math><span style="color:black">:</span>
  
−
== Faktorisering av 2:a gradspolynom ==
+
:::<math> \quad x^2 - 6\,x + 9 \; = \; (x-3)^2 \; = \; \boxed{(x-3) \cdot (x-3)} </math>
  
−
Sätter man polynomet <math> x^2 - 7\,x + 12 </math> till 0 uppstår följande ekvation:
+
<math> (x-3) \cdot (x-3) \, </math> kallas för polynomet <math> \, x^2 - 6\,x + 9 \, </math> i <b><span style="color:red">faktorform</span></b>.
  
−
::::::::::<math> x^2 - 7\,x + 12 = (x-3) \cdot (x-4) = 0 </math>
+
Samtidigt är <math> \, x=3 \, </math> polynomets enda nollställe, en s.k. [[1.2_Faktorisering_av_polynom#Dubbelrot|<b><span style="color:blue">dubbelrot</span></b>]].
 +
</div>
  
−
Denna ekvation är en inbjudan att söka de tal x för vilka polynomets värde är 0. Du minns väl att man kallar sådana x för polynomets <span style="color:red">nollställen</span>. Därför är denna ekvations lösningar identiska med polynomets nollställen, vare sig man skriver polynomet som en summa av termer eller i faktorform. Faktorformen <math>(x-3) (x-4) </math> har dock den stora fördelen att man kan se lösningarna till ekvationen ovan utan att behöva räkna. Det är <span style="color:red">nollproduktmetoden</span> som gör detta möjligt. Den visar nämligen att 3 och 4 är lösningar till ekvationen <math> (x-3) (x-4) = 0 </math>: För att produkten <math> (x-3) (x-4) </math> ska vara lika med 0 måste antingen den första faktorn <math> (x-3) </math> eller den andra faktorn <math> (x-4) </math> vara lika med 0. För att <math> (x-3) </math> eller <math> (x-4) </math> ska vara lika med 0 måste <math> x </math> antingen vara lika med 3 eller lika med 4. Detta i sin tur innebär att 3 och 4 är lösningar till ekvationen <math> (x-3) (x-4) = 0 </math>. Å andra sidan måste pga likheten mellan polynom och dess faktorform 3 och 4 även vara polynomets nollställen dvs lösningar till ekvationen ovan. Men vad gör man om man inte än har faktorformen?
 
  
−
Resonemanget ovan ger oss nu en metod i handen for att få fram faktorformen från polynomet. För att faktorisera polynomet<math> x^2 - 7\,x + 12 </math> behöver vi bara beräkna dess nollställen, säg x1 och x2, och sedan skriva upp faktorformen <math>(x-x1) (x-x2) </math>. Låt oss genomföra det i vårt exempel:
+
<big>
 +
Självklart hade kvadreringsregeln inte fungerat om det istället för <math> \, - 6\,x \, </math> i polynomets andra term hade stått t.ex. <math> \, - 7\,x \, </math>,
  
−
::::::::::<math>\begin{align} x^2 - 7\,x + 12 & = 0                          \\
+
för visserligen är <math> \, - 7\,x = - 2 \cdot x \cdot 3,5 \, </math>, men det går inte ihop med nästa term <math> \, b\,^2 \, </math> i kvadreringsregeln: Vi kan inte ha <math> \, 3,5 \, </math> som <math> \, b \, </math>, därför att <math> \, (3,5)^2 \neq 9  \, </math>.
−
                                      x_{1,2} & = 3,5 \pm \sqrt{12,25 - 12}  \\
+
−
                                      x_{1,2} & = 3,5 \pm \sqrt{0,25}        \\
+
−
                                      x_{1,2} & = 3,5 \pm 0,5                \\
+
−
                                      x_1    & = 4                          \\
+
−
                                      x_2    & = 3                         \\
+
−
          \end{align}</math>
+
  
−
Därför har polynomet <math> x^2 - 7\,x + 12 </math> faktorformen <math> (x-3) \cdot (x-4) </math>. Vi kommer att lära oss en effektivare metod för lösning av 2:a gradsekvationer och därmed för faktorisering av 2:gradspolynom, när vi lärt oss ett enkelt samband mellan ett polynoms koefficienter och dess nollställen (Vietas formler).
+
Så, exemplet ovan var tillrättalagt så att kvadreringsregeln kunde fungera. Ett litet annorlunda polynom, t.ex. <math> \, x^2 - 7\,x + 9 \, </math> kan inte längre faktoriseras genom
  
−
Det som vi genomförde för vårt exempel kan generaliseras till alla 2:gradspolynom, åtminstone sådana som är givna i normalform:
+
att använda konjugat- eller kvadreringsreglerna baklänges. Dessa regler kan faktorisera endast en liten del av väldigt speciella 2:a gradspolynom.
  
−
'''Sats (Faktorisering 2 nollställen)''':
+
I själva verket kan alla polynom faktoriseras, vilket vi kommer att lära oss nu:
−
::::<big>Om 2:gradspolynomet <math> x^2 + p\,x + q </math> har nollställena <math> x_1\, </math> och <math> x_2\, </math> så gäller:</big>
+
</big>
  
−
::::::::::<math> x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) </math>
+
== <b><span style="color:#931136">Polynom i faktorform</span></b> ==
  
−
För att bevisa satsen ovan kan man t.ex. sätta in 2:a gradsekvationens lösningsformel (pq-formeln) för <math> x_1\, </math> och <math> x_2\, </math> och utveckla produkten på högerledet. En jämförelse av koefficienter kommer att resultera i likhet med vänsterledet. Det finns motsvarande satser om polynom av högre grad än 2 som vi inte behandlar här.
 
  
−
Istället ska vi undersöka ett enkelt, men intressant samband mellan 2:a gradspolynomets koefficienter <math> p\, </math> och <math> q\, </math> och dess nollställen <math> x_1\, </math> och <math> x_2\, </math>, vilket ger dig möjligheten att roa dina vänner genom att låta dem säga två tal, t.ex. 3 och 4, och omedelbart skriva upp den 2:a gradsekvation vars lösningar just är 3 och 4.
+
=== <b><span style="color:#931136">Exempel</span></b> ===
  
−
== Samband mellan koefficienter och nollställen ==
+
<div class="border-divblue"> <!-- border-divblue1 -->
 +
I förra avsnitt lärde vi oss att ett polynom var en <b><span style="color:red">summa</span></b> av termer.
  
−
Vi åter anknyter till likheten mellan polynom och dess faktorform som vi behandlade ovan (Faktorisering av 2: gradspolynom) genom att utveckla produkten:
+
Visa att följande <b><span style="color:red">produkt</span></b> är ett polynom:
  
−
::::<math> (x-3) \cdot (x-4) = x^2 - 4\,x - 3\,x + 3 \cdot 4 = x^2 - (3+4)\,x + 3 \cdot 4 = x^2 - 7\,x + 12 </math>
+
:::<math> (x-3) \, \cdot \, (x-4) </math>
  
−
Att vi i mellanräkningen, till synes onödigt, skriver <math> x^2 - (3+4)\,x + 3 \cdot 4 </math> beror på att vi vill förtydliga sambandet mellan polynomets koefficienter -7 och 12 å ena sidan och dess nollställen 3 och 4 å andra sidan: x-termens koefficient -7 är summan av 3 och 4 med omvänt förtecken. Polynomets konstanta term 12 är produkten till 3 och 4, dvs:
+
Vi utvecklar produkten:
  
−
:::::::::::<math> 3 + 4 = 7 \qquad {\rm och} \qquad 3 \cdot 4 = 12 </math>
+
::<math> (x-3) \, \cdot \, (x-4) \; = \; x^2 \, - \, 4\,x - \, 3\,x \, + \, 3 \cdot 4 \; = \; \underline{x^2 \, - \, 7\,x \, + \, 12} \; </math>
 +
</div>  <!-- border-divblue1 -->
  
−
På så sätt kan du roa dina vänner genom att låta dem säga två tal, t.ex. 3 och 4, och omedelbart skriva upp 2:a gradsekvationen
+
::::::::::::::<big><math> \Downarrow </math></big>
  
−
:::::::::::::<math> x^2 - 7\,x + 12 = 0 </math>
+
<div class="ovnC">
−
+
<math> \; (x-3) \cdot (x-4) \; </math> kallas för polynomet <math> \; x^2 - 7\,x + 12 \; </math> <b><span style="color:red"> i faktorform</span></b>.
−
och låta dina vänner lösa ekvationen. De kommer att få just dessa två tal som lösningar. För att bilda ekvationen behöver du bara summera talen och sätta summan med omvänt förtecken framför x samt multiplicera talen med varandra och använda produkten som 2:a gradsekvationens konstanta term. Prova gärna med andra tal. Det kommer alltid att stämma, vilket inte är något trolleri utan resultat av följande generell matematisk sats:
+
  
−
'''Sats (Vietas formler)''':
+
<math> \qquad\;\, 3 \;\;\; </math> och <math> \;\;\, 4 \;\; </math> är polynomets nollställen, se nollproduktmetoden:
−
::::<big>Om 2:gradspolynomet <math> x^2 + p\,x + q </math> har nollställena <math> x_1\, </math> och <math> x_2\, </math> så gäller:</big>
+
</div>
  
−
:::::::::<math> x_1 + x_2 = -p \qquad {\rm och} \qquad x_1 \cdot x_2 = q </math>
 
  
−
'''Bevis''':
+
== <b><span style="color:#931136">Nollproduktmetoden</span></b> ==
 +
<div class="ovnE">
 +
Lös ekvationen<span style="color:black">:</span> <math> \qquad\qquad\qquad\;\:(x-3) \, \cdot \, (x-4) \; = \; 0 </math>
  
−
Genom att använda satsen som vi formulerade i slutet av förra paragrafen (Faktorisering 2 nollställen) kan vi skriva:
+
:<math> {\rm {\color{Red} {OBS!\quad Vanlig\;fel\;åtgärd:}}} \quad\; (x-3) \cdot (x-4) \; = \; x^2 - 4\,x - 3\,x + 3 \cdot 4 \; = \; x^2 \, - \, 7\,x \, + \, 12 \; = \; 0  </math>
  
−
::::::::::<math> x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) </math>
+
:<math> \qquad\quad\; {\rm Rätt\;åtgärd: \qquad\quad\; Räkna\;inte!\quad Tänk\;istället\;sä\;här:} </math>
  
−
Om vi nu utvecklar produkten på höger sidan kan vi skriva vidare:
+
För att <math> \, (x-3) \cdot (x-4) \, </math> ska vara <math> 0 </math>, måste antingen <math> \, (x-3) \, </math> eller <math> \, (x-4) \, </math> vara <math> \, 0 \; </math><span style="color:black">:</span> <math> \quad a \cdot b = 0 \;\; \Rightarrow \;\; a = 0 \; </math> eller <math> \; b = 0  </math>
  
−
::<math> x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) = x^2 - x_2\,x - x_1\,x + x_1 \cdot x_2 = x^2 - (x_1+x_2)\,x + x_1 \cdot x_2 </math>
+
För att <math> \, (x-3) \, </math> eller <math> \, (x-4) \, </math> ska vara <math> \, 0 \,</math> måste <math> \, x \, </math> antingen vara <math> \, 3 \, </math> eller <math> \, 4 </math>.
  
−
En jämförelse av koefficienterna mellan polynomet <math> x^2 - (x_1+x_2)\,x + x_1 \cdot x_2 </math> (högerledet) och polynomet <math> x^2 + p\,x + q </math> (vänsterledet) ger resultatet:
+
<table>
 +
<tr>
 +
<td>Alltså har ekvationen de två lösningarna:
  
−
:::::::::<math> x_1 + x_2 = -p \qquad {\rm och} \qquad x_1 \cdot x_2 = q </math>
 
  
−
Vad som skulle bevisas (V.s.b.).
+
</td>
 +
<td><math>\qquad\begin{align}  x_1 & = 3  \\
 +
                              x_2 & = 4
 +
                \end{align} </math>
 +
</td>
 +
</tr>
 +
</table>
 +
<b><span style="color:red">Nollproduktmetoden</span></b> ger oss ekvationens lösningar utan att vi behöver räkna!
  
−
Även denna sats kan generaliseras till polynom av högre grad än 2. Den franske matematikern [http://en.wikipedia.org/wiki/Fran%C3%A7ois_Vi%C3%A8te François Viète|](1540-1603) var en av de första som såg sambandet mellan ett polynoms koefficienter och dess nollställen. Därför kallas formlerna <math> x_1 + x_2 = -p\, </math> och <math> x_1 \cdot x_2 = q </math> efter honom <span style="color:red">Vietas formler</span>.
+
Den felaktiga åtgärden ovan är formellt matematiskt inte fel, men är ineffektiv och förstör faktorformen.
  
−
Er stor fördel av Vietas formler för oss är att man kan lösa 2:a gradsekvationer och därmed faktorisera polynom utan att behöva använda lösningsformeln. Detta innebär mindre räknearbete vilket i sin tur minskar risken för felräkning. På köpet går det fortare att ta fram polynomens faktorform.
+
Faktorformen är den struktur som gör nollproduktmetoden och därmed den effektiva lösningen möjlig.
 +
</div>
  
−
===== Exempel 1 =====
 
  
−
Ta ekvationen
+
<big>
 +
Ett polynom i faktorform visar sina <b><span style="color:red">nollställen</span></b> istället för koefficienterna.
  
−
<math> x^2 - 7\,x + 10 = 0 </math>
+
Men hur får man faktorformen om man har polynomet som en summa av termer? Man måste bestämma nollställena:
 +
</big>
  
−
För lösningarna <math> x_1\,</math> och <math> x_2\,</math> måste enligt Vietas formler gälla:
 
  
−
<math> \begin{align} x_1  +  x_2 & = -(-7) = 7  \\
+
== <b><span style="color:#931136">Faktorisering av 2:a gradspolynom (normalform)</span></b> ==
−
                      x_1 \cdot x_2 & = 10
+
−
        \end{align}</math>
+
  
−
Vi måste alltså hitta två tal vars produkt är 10 och vars summa är 7. Med lite provande hittar man 2 und 5 eftersom <math> 2 + 5 = 7\, </math> och <math> 2 \cdot 5 = 10 </math>. Prövning bekräftar resultatet.
+
<div class="border-divblue"> <!-- border-divblue2 -->
 +
<div class="exempel">
 +
<b><span style="color:#931136">Uppgiften:</span></b> Faktorisera polynomet <math> \, x^2 - 7\,x + 12 </math>.
  
−
Har vi på det här enkla sättet hittat nollställena till polynomet <math> x^2 - 7\,x + 10 </math> kan vi skriva upp faktorformen:
+
<b><span style="color:#931136">Lösningen:</span></b> Vi beräknar polynomets nollställen<span style="color:black">:</span>
  
−
<math> x^2 - 7\,x + 10 = (x - 2) \cdot (x - 5) </math>
+
::::::<math> x^2 - 7\,x + 12 = 0 </math>
  
−
Utveckling av produkten på höger sidan bekräftar faktoriseringen.
+
För att snabbt lösa denna 2:a gradsekvation som ett led i faktoriseringsprocessen
  
−
===== Exempel 2 =====
+
använder vi [[1.2 Repetition: Faktorisering och Vietas formler#Vietas_formler|<b><span style="color:blue">Vietas formler</span></b>]]<span style="color:black">:</span>
  
−
Till ekvationen
+
::::::<math> \begin{align} x_1  +  x_2 & = -p = -(-7) = 7  \\
 +
                          x_1 \cdot x_2 & = \;\;\; q = 12
 +
            \end{align}</math>
  
−
<math> x^2 - 6\,x + 9 = 0 </math>
+
Dvs vi behöver hitta två tal vars produkt är <math> \, 12 \, </math> och vars summa är <math> \, 7 \, </math>.
  
−
ger Vietas formler:
+
Med lite provande kommer man fram till<span style="color:black">:</span>
  
−
<math> \begin{align} x_1   +  x_2 & = -(-6) = 6  \\
+
::::::<math>\begin{align} x_1 & = 3  \\
−
                      x_1 \cdot x_2 & = 9
+
                          x_2 & = 4
−
        \end{align}</math>
+
              \end{align}</math>
  
−
Man hittar lösningarna <math> x_1 = 3\,</math> och <math> x_2 = 3\,</math> eftersom <math> 3 + 3 = 6\,</math> och <math> 3 \cdot 3 = 9 </math>.
+
eftersom <math> \, 3 + 4 = 7 \, </math> och <math> \, 3 \cdot 4 = 12 </math>. Därmed är polynomets <b><span style="color:red">faktorisering</span></b><span style="color:black">:</span>
  
−
Därför kan polynomet <math> x^2 - 6\,x + 9 </math> faktoriseras så här:
+
::::::<math> x^2 - 7\,x + 12 \; = \; \underline{(x - 3) \, \cdot \, (x - 4)} </math>
 +
</div>  <!-- exempel -->
 +
</div> <!-- border-divblue2 -->
  
−
<math> x^2 - 6\,x + 9 = (x - 3) \cdot (x - 3) = (x - 3)^2 </math>
 
  
−
Det intressanta med detta exempel är att vi endast har en lösning x = 3 till 2:a gradsekvationen <math> x^2 - 6 x + 9 = 0 </math>. Fast, om vi tittar på faktorformen <math> (x - 3) (x - 3) = 0 </math> kan man lika bra säga att vi har två identiska lösningar - en filosofisk skillnad som man matematiskt brukar lösa upp genom att kalla lösningen för en <span style="color:red">dubbelrot</span> till ekvationen.
+
<big>
 +
Självklart hade man kunnat använda även [[Media: Formelsamling_NP_Ma3.pdf|<b><span style="color:blue">pq-formeln</span></b>]] för att lösa 2:a gradsekvationen. Då hade det sett ut så här<span style="color:black">:</span>
  
−
== Dubbelrot ==
+
::::::<math>\begin{array}{rcl} x^2 - 7\,x + 12 & = & 0                          \\
 +
                                      x_{1,2} & = & 3,5 \pm \sqrt{12,25 - 12}  \\
 +
                                      x_{1,2} & = & 3,5 \pm \sqrt{0,25}        \\
 +
                                      x_{1,2} & = & 3,5 \pm 0,5                \\
 +
                                      x_1    & = & 3                          \\
 +
                                      x_2    & = & 4                         
 +
            \end{array}</math>
  
−
'''Sats (Faktorisering 1 nollställe)''':
+
Man ser att Vieta inte bara är en enklare och snabbare metod än pq-formeln utan även minimerar risken för felräkning.
−
::::<big>Om 2:gradspolynomet <math> x^2 + p\,x + q </math> endast har ett nollställe <math> x_1\, </math> så gäller:
+
  
−
:::::::::::<math> x^2 + p\,x + q = (x-x_1)^2 </math>
+
Faktorformen (produkten) är resultat av faktorisering (processen).
 +
Exemplets polynom är av grad <math> \, 2</math>, medan dess ingredienser dvs faktorerna <math> \, (x-3) \, </math> och <math> \, (x-4) \, </math> är polynom av grad <math> \, 1</math>.
  
−
::::Ett sådant nollställe kallas för <span style="color:red">dubbelrot</span> till ekvationen <math> x^2 + p\,x + q = 0 </math>.</big>
+
Detta kan jämföras med faktoriseringen <math> \, 12 \, = \, 3 \cdot 4 </math>, där faktorerna <math> \, 3 \, </math> och <math> \, 4 \, </math> är mindre än <math> \, 12 \, </math>. Man har splittrat upp talet <math> \, 12 \,</math> i sina beståndsdelar <math> \, 3 \, </math> och <math> \, 4 </math>, precis som man
  
−
Dubbelrötter har vissa intressanta egenskaper. Låt oss börja att upptäcka dem genom att rita grafen till polynomfunktionen och undersöka på vilket sätt dubbelroten "skär" x-axeln. Vi tar polynomet från Exempel 2 ovan där ekvationen <math> x^2 - 6\,x + 9 = 0 </math> hade dubbelroten x = 3.  
+
splittrar upp polynomet <math> \, x^2 - 7\,x + 12 \, </math> i sina beståndsdelar <math> \, (x-3)\, </math> och <math> \, (x-4) </math>.
  
−
Så här ser grafen ut till polynomfunktionen <math> y = x^2 - 6\,x + 9 </math>:
+
Faktorisering är relevant av olika skäl: För det första tillåter faktorformen förkortning och därmed förenkling av komplexa algebraiska uttryck. För det andra avslöjar faktorformen polynomets [[1.1_Polynom#Ett_polynoms_nollst.C3.A4llen.2C_.C3.A4ven_kallade_r.C3.B6tter|<b><span style="color:blue">nollställen</span></b>]].
  
−
[[Image: Dubbelrot_70.jpg]]
+
Det vi genomförde för vårt exempel kan generaliseras till alla 2:gradspolynom, åtminstone sådana som är givna i normalform:
  
−
Grafen visar att kurvan inte skär utan bara berör x-axeln vid x = 3. Det är en av de typiska egenskaperna hos dubbelrötter. De ligger på gränsen mellan att skära (två lösningar) och inte skära x-axeln (ingen lösning alls). Matematiskt uttrycker sig denna egenskap i faktoriseringens form:
+
<big><b><span style="color:#931136">Sats:</span></b></big></big>
  
−
:::::::::::<math> x^2 - 6\,x + 9 = (x-3) \cdot (x-3) = (x-3)^2 </math>
+
<div class="border-divblue">
 +
== <small><b><span style="color:#931136">Faktorisering med 2 nollställen</span></b></small> ==
  
−
Den dubbla förekomsten av faktorn (x-3) ger roten dess namn dubbelrot.
+
Om 2:a gradspolynomet <math> x^2 + p\,x + q </math> har nollställena <math> x_1\, </math> och <math> x_2\, </math> så gäller:
  
−
== Det allmänna fallet (icke-normalform) ==
+
:::::<math> x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) </math>
 +
</div>
  
−
Alla våra hittills behandlade polynom var i normalform, dvs den ledande koefficienten (kvadratiska termens koefficient eller talet framför x²) var alltid 1. Det behöver inte alltid vara så. Låt oss t.ex. faktorisera följande polynom med ledande koefficienten 3:
+
<big>
 +
För att bevisa satsen ovan kan man t.ex.
  
−
:::::::::::::::::<math> 3\,x^2 - 6\,x - 9 </math>
+
* &nbsp;&nbsp; sätta in [[Media: Formelsamling_NP_Ma3.pdf|<b><span style="color:blue">pq-formeln</span></b>]] för <math> x_1\, </math> och <math> x_2\, </math> i högerledet,
 +
* &nbsp;&nbsp; utveckla produkten på högerledet och
 +
* &nbsp;&nbsp; genomföra [[1.1_Fördjupning_till_Polynom#J.C3.A4mf.C3.B6relse_av_koefficienter|<b><span style="color:blue">jämförelse av koefficienter</span></b>]].
  
−
Lösningen består i att återföra problemet till den kända typen i normalform genom att bryta ut den ledande koefficienten:
+
Se beviset i lösningen till [[1.2_Övningar_till_Faktorisering_av_polynom#.C3.96vning_13|<b><span style="color:blue">övning 13</span></b>]].
  
−
::::::::::<math> 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) = 3\,(x-x_1) \cdot (x-x_2) </math>
+
Det finns motsvarande satser om polynom av högre grad än 2, se  [[1.2_Fördjupning_till_Faktorisering_av_Polynom#Algebrans_fundamentalsats|<b><span style="color:blue">Algebrans fundamentalsats</span></b>]].
 +
</big>
  
−
där <math>(x-x_1) \cdot (x-x_2)</math> är faktoriseringen av polynomet <math> x^2 - 2\,x - 3 </math>. Efter att ha löst detta nya problem kan vi komma tillbaka och sätta in lösningen i ansatsen ovan för att få faktoriseringen av <math> 3\,x^2 - 6\,x - 9 </math>.
+
<big><big><b><span style="color:#931136">Praktisk slutsats:</span></b></big></big>
 +
<div class="ovnE">
 +
För att faktorisera ett 2:a gradspolynom i normalform måste vi beräkna dess
  
−
För att få fram <math> x_1\,</math> och <math> x_2\,</math> som ger oss faktoriseringen av <math> x^2 - 2\,x - 3 </math> kan vi som vanligt använda Vietas formler:
+
nollställen <math> x_1\, </math> och <math> x_2\, </math>. Sedan blir faktoriseringen<span style="color:black">:</span> <math> \quad (x-x_1) \cdot (x-x_2) </math>
 +
</div>
  
−
<math> \begin{align} x_1  +  x_2 & = -(-2) = 2  \\
 
−
                      x_1 \cdot x_2 & = -3
 
−
        \end{align}</math>
 
  
−
Man hittar lösningarna <math> x_1 = 3\,</math> och <math> x_2 = -1\,</math> eftersom <math> 3 + (-1) = 2\,</math> och <math> 3 \cdot (-1) = -3 </math>.
+
== <b><span style="color:#931136">Rotens olika betydelser</span></b> ==
  
−
Därför kan polynomet <math> x^2 - 2\,x - 3 </math> faktoriseras så här:
+
<big>
 +
Ordet <b><span style="color:red">rot</span></b> har i matematiken olika betydelser i olika sammanhang:
  
−
<math> x^2 - 2\,x - 3 = (x - 3) \cdot (x + 1) </math>
+
# &nbsp;&nbsp; Räkneoperationen rotdragning med rottecknet <math> {\color{White}{y=}}\!\!\!\!\!\!\!\!\sqrt{\color{White}x} </math> som symbol, t.ex. roten ur <math> 4\, </math> är <math> 2\, </math> osv.
 +
# &nbsp;&nbsp; Lösningen av en ekvation. Rot är synonym till en ekvations lösning. T.ex. är <math> x_1 = 2\, </math> och <math> x_2 = -2\, </math> rötter dvs lösningar till ekvationen <math> x^2 = 4\, </math>.
 +
# &nbsp;&nbsp; Nollstället till ett polynom. Rot är synonym till ett polynoms nollställe. I exemplet ovan är <math> x_1 = 2\, </math> och <math> x_2 = -2\, </math> rötter dvs nollställen till polynomet <math> x^2 - 4\, </math>.
  
−
Går vi tillbaka och sätter in denna lösning i det ursprungliga problemets ansats får vi det ursprungliga polynomets faktorisering:
+
Sammanhanget avgör vilken betydelse som gäller just i den aktuella kontexten.
 +
</big>
  
−
::::::::::<math> 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) = 3\,(x-3) \cdot (x+1) </math>
 
  
−
Den ovan beskrivna metoden fungerar alltid när 2:a gradspolynomet har ett eller två nollställen. Har det däremot inget nollställe alls finns det inte heller någon faktorisering.
+
== <b><span style="color:#931136">Dubbelrot</span></b> ==
  
−
===== Exempel 3 =====
+
<big>
 +
När vi nu i fortsättningen pratar om en dubbelrot menar vi två lösningar till en ekvation som sammanfaller, vilket även kan uppfattas som endast en lösning.
  
−
Vad gör man om den ledande koefficienten "inte går att bryta ut" eftersom den inte delar de andra koefficienterna jämnt? Man gör det ändå och går över till tal i bråkform. Det finns nämligen ingen begränsning varken för polynomets nollställen eller koefficienter, när det gäller taltypen: De kan vara heltal, som var fallet hittills i våra exempel, men även bråk- eller decimaltal. Låt oss t.ex. faktorisera följande polynom med en ledande koefficient som inte delar de andra koefficienterna jämnt:
+
<big><b><span style="color:#931136">Sats:</span></b></big></big>
  
−
:::::::::::::::::<math> 7\,x^2 - 5\,x - 2 </math>
+
<div class="border-divblue">
  
−
Vi bryter ut 7 och skriver det nya polynomets koefficienter i bråkform:
+
== <small><b><span style="color:#931136">Faktorisering med 1 nollställe</span></b></small> ==
  
−
::::::::::<math> 7\,x^2 - 5\,x - 2 = 7\,(x^2 - {5 \over 7}\,x - {2 \over 7}) = 7\,(x-x_1) \cdot (x-x_2) </math>
+
Om 2:gradspolynomet <math> x^2 + p\,x + q </math> endast har ett nollställe <math> x_1\, </math> så gäller:
  
−
För att få fram <math> x_1\,</math> och <math> x_2\,</math> använder vi Vietas formler:
+
:::::::<math> x^2 + p\,x + q = (x-x_1)^2 </math>
  
−
<math> \begin{align} x_1  +   x_2 & = {5 \over 7}  \\
+
Ett sådant nollställe kallas för <b><span style="color:red">dubbelrot</span></b> till ekvationen <math> x^2 + p\,x + q = 0 </math>.
−
                    x_1 \cdot x_2 & = - {2 \over 7}
+
</div>
−
        \end{align}</math>
+
  
−
Man hittar lösningarna <math> x_1 = 1\,</math> och <math> x_2 = -{2 \over 7}\,</math> eftersom <math> 1 - {2 \over 7} = {5 \over 7} </math> och <math> 1 \cdot {-2 \over 7} = {-2 \over 7} </math>.
 
  
−
Så får vi det nya polynomets faktorisering:
+
<div class="exempel">
 +
== <b><span style="color:#931136">Exempel</span></b> ==
 +
<big>
 +
Polynomet <math> x^2 - 6\,x + 9 </math> har dubbelroten <math> x = 3\, </math> eftersom <math> x^2 - 6\,x + 9 \, = \, (x-3)\,^2 </math>, se [[1.2 Repetition: Faktorisering och Vietas formler#Enkel faktorisering_av_polynom|<b><span style="color:blue">Enkel faktorisering av polynom</span></b>]].
  
−
<math> x^2 - {5 \over 7}\,x - {2 \over 7} = (x - 1) \cdot (x + {2 \over 7}) </math>
+
Vi ritar grafen till polynomfunktionen och undersöker på vilket sätt kurvan "skär" <math> \, x</math>-axeln.
  
−
Går vi tillbaka och sätter in detta i det ursprungliga problemets ansats får vi det ursprungliga polynomets faktorisering:
+
<big>Grafen till polynomfunktionen</big> <math> \; y = x^2 - 6\,x + 9 \; {\rm :} \quad\quad </math> [[Image: Dubbelrot.jpg]]
  
−
::::::::::<math> 7\,x^2 - 5\,x - 2 = 7\,(x^2 - {5 \over 7}\,x - {2 \over 7}) = 7\,(x - 1) \cdot (x + {2 \over 7}) </math>
+
Grafen visar att kurvan inte skär utan bara <b><span style="color:black">berör</span></b> <math>\,x</math>-axeln vid <math> x = 3\, </math>.
  
−
Vill man i slutet bli av med bråktal kan man multiplicera in 7 i den andra parentesen och skriva faktoriseringen så här:
+
Dvs det finns endast <b><span style="color:black">en</span></b> gemensam punkt mellan kurvan och <math>\,x</math>-axeln.
  
−
:::::::::::::<math> 7\,x^2 - 5\,x - 2 = (x - 1) \cdot (7\,x + 2) </math>
+
Dubbelrötter ligger på gränsen mellan att skära (två lösningar) och inte skära <math>\,x</math>-axeln (ingen lösning alls).
  
−
== Faktorisering av 3:e och högre gradspolynom ==
+
Matematiskt uttrycker sig detta i faktoriseringens form:
  
−
Faktorisering av 2:a gradspolynom är alltid möjlig för oss eftersom vi kan lösa 2:a gradsekvationer. I de fall man lyckas återföra 3:e eller högre gradsekvationer till 2:a gradsekvationer är det även möjligt att faktorisera polynom av högre grad än 2. Ett sådant fall föreligger om man antingen känner till eller t.ex. med hjälp av grafen kan få fram åtminstone en lösning till en 3:e gradsekvation. Låt oss genomföra detta för följande exempel:
+
::::::<math> x^2 - 6\,x + 9 = (x-3) \cdot (x-3) = (x-3)\,^2 </math>
 +
</big></div>
  
−
'''Problem:''' Faktorisera 3:e gradspolynomet
+
<big>
 +
Det intressanta med dubelrötter är att vi endast har <b>en</b> lösning <math> x = 3\, </math> till 2:a gradsekvationen <math> x^2 - 6 x + 9 = 0\, </math>. Fast, om vi tittar på faktorformen <math> (x - 3) \cdot (x - 3) = 0 </math> kan man lika bra säga
  
−
:::::::<math> P(x) = x^3 - 6\,x^2 + 5\,x + 12 </math>
+
att vi har två identiska lösningar eller två som sammanfaller - ett filosofiskt dilemma som man matematiskt brukar lösa upp genom att kalla lösningen för en dubbelrot.
  
−
'''Lösning:''' För att få fram något av polynomets nollställen ritar vi  
+
Andra viktiga egenskaper av dubbelrötter kommer vi att lära känna senare när vi i kapitel 2 behandlar derivering.
−
 
+
−
grafen till funktionen <math> y = x^3 - 6\,x^2 + 5\,x + 12 </math>
+
−
 
+
−
[[Image: 3e_gradspolynom_70.jpg]]
+
−
 
+
−
Grafen visar att polynomet har tre nollställen av vilka ett är ganska tydligt på bilden och kan avläsas till x = -1, medan de andra två är mindre tydliga. För att avgöra om detta nollställe är exakt gör vi en prövning genom att sätta in x = -1 i polynomet:
+
−
 
+
−
<math> P(-1) = (-1)^3 - 6\,\cdot\,(-1)^2 + 5\,\cdot\,(-1) + 12 = -1 - 6\,\cdot\,1 - 5 + 12 = -1 -6 -5 +12 = -12 +12 = 0 </math>
+
−
 
+
−
Prövningen visar att x = -1 är ett exakt nollställe till P(x). Härav kan vi nu dra slutsatsen att de två andra nollställena måste uppfylla följande ekvation:
+
−
 
+
−
:::::::<math> P(x) = x^3 - 6\,x^2 + 5\,x + 12 = Q(x) \cdot (x+1) = 0 </math>
+
−
 
+
−
där <math> Q(x) </math> är ett 2:a gradspolynom som vi inte känner till än. Denna slutsats baseras på en generell matematisk sats, algebrans fundamentalsats som säger att ett polynom av grad n har n nollställen. Vi kan med nollproduktmetoden resonera så här: För att produkten <math> Q(x) \cdot (x+1) </math> ska vara lika med 0 måste antingen <math> Q(x) </math> eller <math> (x+1) </math> vara lika med 0. Vi vet redan att <math> (x+1) </math> är 0 för x = -1  som är <math> P(x) </math>:s ena nollställe. Alltså måste <math> P(x) </math>:s andra två nollställen finnas i <math> Q(x) </math>. Med andra ord de andra två nollställen måste vara det 2:a gradspolynomet <math> Q(x) </math>:s nollställen. Kan vi bestämma <math> Q(x) </math>, beräkna dess nollställen samt ställa upp dess faktorform, har vi faktoriserat även det 3:e gradspolynomet <math> P(x) </math>. Vi har ju redan hittat ett nollställe och ställt upp en ansats till faktoriseringen av <math> P(x) </math> i form av ekvationen ovan. Vi bearbetar nu vidare denna ansats genom att införa i den för <math> Q(x) </math> den allmänna formen för ett 2:a gradspolynom:
+
−
 
+
−
<math> Q(x) = a\,x^2 + b\,x + c </math>
+
−
 
+
−
där a, b och c är koefficienter som vi måste bestämma. Sätter vi in denna form i ansasten ovan får vi:
+
−
 
+
−
::::::<math> x^3 - 6\,x^2 + 5\,x + 12 = (a\,x^2 + b\,x + c) \cdot (x+1) </math>
+
−
 
+
−
Vi vet från förra avsnitt att två polynom är lika med varandra om alla deras motsvarande koefficienter, dvs de som tillhör termer av samma grad, överensstämmer. För att kunna genomföra denna jämförelse av koefficienter utvecklar vi produkten på höger sidan och ordnar termerna:
+
−
 
+
−
::<math> x^3 - 6\,x^2 + 5\,x + 12 = a\,x^3 + b\,x^2 + c\,x + a\,x^2 + b\,x + c = a\,x^3 + (b+a)\,x^2 + (c+b)\,x + c </math>
+
−
 
+
−
Jämförelse av koefficienterna på höger- och vänsterled ger:
+
−
 
+
−
::<math> \begin{align} a    & = 1    \\
+
−
                      b + a & = -6  \\
+
−
                      c + b & = 5    \\
+
−
                      c    & = 12
+
−
        \end{align}</math>
+
−
 
+
−
Genom insättning av <math> a = 1 </math> i den andra och <math> c = 12 </math> i den tredje ekvationen får vi i båda fall b = -7. Därmed har vi bestämt polynomet <math>Q(x)</math>:
+
−
 
+
−
<math> Q(x) = x^2 - 7\,x + 12 </math>
+
−
 
+
−
I början av detta avsnitt (Faktorisering av 2:a gradspolynom) hade vi faktoriserat det här polynomet till:
+
−
 
+
−
::::::::<math> x^2 - 7\,x + 12 = (x-3) \cdot (x-4) </math>
+
−
 
+
−
Inför vi nu detta resultat i vår ansats i början får vi faktoriseringen för P(x):
+
−
 
+
−
::<math> P(x) = x^3 - 6\,x^2 + 5\,x + 12 = Q(x) \cdot (x+1) = (x^2 - 7\,x + 12) \cdot (x+1) = (x-3)\,\cdot\,(x-4)\,\cdot\,(x+1) </math>
+
−
 
+
−
Den ovan beskrivna metoden kan i princip även användas för faktorisering av polynom av högre grad än 3. Anledningen till det är algebrans fundamentalsats som vi redan nämnde tidigare och som lite förenklad lyder så här:
+
−
 
+
−
'''Sats (Algebrans fundamentalsats)''':
+
−
::::<big>Ett polynom av grad n har exakt n nollställen <math> x_1, \, x_2, \,\quad\ldots\, x_n </math>och kan faktoriseras så här:
+
−
 
+
−
:::::<math> a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + \quad \ldots \quad + a_1 \cdot x + a_0\;=\;a_n \cdot (x-x_1) \cdot (x-x_2) \cdot\quad\ldots\quad \cdot (x-x_n) </math>
+
 
</big>
 
</big>
−
Några anmärkningar måste göras till denna förenklade formulering av algebrans fundamentalsats:
 
−
* Egentligen utgör endast den första delen (polynom av grad n har exakt n nollställen) algebrans fundamentalsats. Den andra delen om faktorisering är en följd av den.
 
−
* Antalet n nollställen är räknade med multiplicitet, dvs dubbla rötter är räknade två gånger, tredubbla tre gånger osv.
 
−
* Den fullständiga faktoriseringen i linjära faktorer <math> (x-x_i)\, </math> är endast möjlig i mängden av s.k. komplexa tal, en taltyp som inte behandlas i C-kursen. För oss som räknar med reella tal (största taltyp vi känner till) betyder der att vissa polynom endast kan faktoriseras till linjära och kvadratiska faktorer.
 
  
−
===== Exempel 4 =====
 
  
−
<math> P(x) = x^5 - 5\,x^4 + 17\,x^3 - 13\,x^2 = x\cdot x\cdot (x-1)\cdot (x^2 - 4\,x + 13) </math>
 
  
−
Polynomet P(x) har en dubbelrot x = 0, en enkel rot x = 1 och två s.k. komplexa rötter som ger upphov till den kvadratiska faktor som står sist. För oss räcker det att ange faktoriseringen i forman ovan. Vi kan få fram den med de metoder vi lärt oss i detta avsnitt: Den dubbla roten x = 0 får vi genom att bryta ut <math> x^2 </math>, roten x = 1 kan vi t.ex. få via grafen samt en prövning. Den kvadratiska faktorns koefficienter kan vi beräkna med hjälp av jämförelse av koefficienter. Att det inte går att få fram en fullständig faktorisering i linjära faktorer beror på att den kvadratiska faktorn saknar reella rötter.
+
== <b><span style="color:#931136">Internetlänkar</span></b> ==
  
−
===== Exempel 5 =====
+
http://tutorial.math.lamar.edu/Classes/Alg/Factoring.aspx
  
−
Att vi ändå kan ha praktisk nytta av algebrans fundamentalsats visar följande exempel: I [[1.1 Övning 6|övning 6]] i avsnittet 1.1 Ekvationer hade vi (förhoppningsvis) löst 4:e gradsekvationen
+
http://mathworld.wolfram.com/PolynomialFactorization.html
  
−
<math> x^4 - 29\;x^2 = -100 </math>
+
http://www.mathsisfun.com/algebra/fundamental-theorem-algebra.html
  
−
och fått lösningarna
+
http://www.sosmath.com/algebra/factor/fac04/fac04.html
  
−
<math> x_1 = 5, \qquad x_2 = -5, \qquad x_3 = 2 \quad {\rm och} \quad x_4 = -2 </math>
+
http://www.lboro.ac.uk/research/helm/C_HELM_backup_24nov03/helm_website/documents/wb03_blk3.pdf
  
−
Vi kan skriva ekvationen som en polynomekvation
 
  
−
<math> P(x) = x^4 - 29\;x^2 + 100 = 0 </math>
 
  
−
Pga kännedomen om ekvationens lösningar som är identiska med polynomets nollställen, kan vi enligt algebrans fundamentalsats faktorisera 4:e gradspolynomet P(x) så här:
 
  
−
<math> P(x) = x^4 - 29\;x^2 + 100 = (x-5) \cdot (x+5) \cdot (x-2) \cdot (x+2) </math>
 
  
−
== Internetlänkar ==
 
−
http://tutorial.math.lamar.edu/Classes/Alg/Factoring.aspx
 
  
−
http://mathworld.wolfram.com/PolynomialFactorization.html
 
  
−
http://www.mathsisfun.com/algebra/fundamental-theorem-algebra.html
 
  
−
http://www.sosmath.com/algebra/factor/fac04/fac04.html
+
[[Matte:Copyrights|Copyright]] © 2019 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved.
−
 
+
−
http://www.lboro.ac.uk/research/helm/C_HELM_backup_24nov03/helm_website/documents/wb03_blk3.pdf
+

Nuvarande version från 2 december 2024 kl. 21.57

        <<  Förra avsnitt          Genomgång          Övningar          Fördjupning          Nästa avsnitt  >>      


Faktorisering av tal

Matte 1:

\( a \cdot b \quad \) är en produkt, där \(a\,\) och \(b\,\) kallas för faktorer.

Därför är t.ex. \( \quad \boxed{12 \, = \, 3 \cdot 4} \quad \) en faktorisering av

talet \( \, 12 \, \) och \( \, 3 \cdot 4 \, \) kallas för en faktorform av talet.

En annan faktorform är \( \, 3 \cdot 2\cdot 2 \, \) (Primfaktorer).


Faktorisering betyder alltså omvandling till en produkt.

Analogt till faktorisering av heltal kan även ett polynom som ursprungligen är en summa av termer, faktoriseras dvs skrivas om till en produkt.


Enkel faktorisering av polynom

Matte 2:

Kvadreringsregeln \( \, (a-b)\,^2 = a^2 - 2\,a\,b + b^2 \, \) ger t.ex.:

\( \qquad\qquad\qquad\quad\;\; (x-3)\,^2 \; = \; x^2 - 2 \cdot x \cdot 3 + 3^2 \; = \; x^2 - 6\,x + 9 \)

Läser vi baklänges får vi en faktorisering av polynomet \( \, x^2 - 6\,x + 9 \, \):

\[ \quad x^2 - 6\,x + 9 \; = \; (x-3)^2 \; = \; \boxed{(x-3) \cdot (x-3)} \]

\( (x-3) \cdot (x-3) \, \) kallas för polynomet \( \, x^2 - 6\,x + 9 \, \) i faktorform.

Samtidigt är \( \, x=3 \, \) polynomets enda nollställe, en s.k. dubbelrot.


Självklart hade kvadreringsregeln inte fungerat om det istället för \( \, - 6\,x \, \) i polynomets andra term hade stått t.ex. \( \, - 7\,x \, \),

för visserligen är \( \, - 7\,x = - 2 \cdot x \cdot 3,5 \, \), men det går inte ihop med nästa term \( \, b\,^2 \, \) i kvadreringsregeln: Vi kan inte ha \( \, 3,5 \, \) som \( \, b \, \), därför att \( \, (3,5)^2 \neq 9 \, \).

Så, exemplet ovan var tillrättalagt så att kvadreringsregeln kunde fungera. Ett litet annorlunda polynom, t.ex. \( \, x^2 - 7\,x + 9 \, \) kan inte längre faktoriseras genom

att använda konjugat- eller kvadreringsreglerna baklänges. Dessa regler kan faktorisera endast en liten del av väldigt speciella 2:a gradspolynom.

I själva verket kan alla polynom faktoriseras, vilket vi kommer att lära oss nu:

Polynom i faktorform

Exempel

I förra avsnitt lärde vi oss att ett polynom var en summa av termer.

Visa att följande produkt är ett polynom:

\[ (x-3) \, \cdot \, (x-4) \]

Vi utvecklar produkten:

\[ (x-3) \, \cdot \, (x-4) \; = \; x^2 \, - \, 4\,x - \, 3\,x \, + \, 3 \cdot 4 \; = \; \underline{x^2 \, - \, 7\,x \, + \, 12} \; \]
\( \Downarrow \)

\( \; (x-3) \cdot (x-4) \; \) kallas för polynomet \( \; x^2 - 7\,x + 12 \; \) i faktorform.

\( \qquad\;\, 3 \;\;\; \) och \( \;\;\, 4 \;\; \) är polynomets nollställen, se nollproduktmetoden:


Nollproduktmetoden

Lös ekvationen: \( \qquad\qquad\qquad\;\:(x-3) \, \cdot \, (x-4) \; = \; 0 \)

\[ {\rm {\color{Red} {OBS!\quad Vanlig\;fel\;åtgärd:}}} \quad\; (x-3) \cdot (x-4) \; = \; x^2 - 4\,x - 3\,x + 3 \cdot 4 \; = \; x^2 \, - \, 7\,x \, + \, 12 \; = \; 0 \]

\[ \qquad\quad\; {\rm Rätt\;åtgärd: \qquad\quad\; Räkna\;inte!\quad Tänk\;istället\;sä\;här:} \]

För att \( \, (x-3) \cdot (x-4) \, \) ska vara \( 0 \), måste antingen \( \, (x-3) \, \) eller \( \, (x-4) \, \) vara \( \, 0 \; \): \( \quad a \cdot b = 0 \;\; \Rightarrow \;\; a = 0 \; \) eller \( \; b = 0 \)

För att \( \, (x-3) \, \) eller \( \, (x-4) \, \) ska vara \( \, 0 \,\) måste \( \, x \, \) antingen vara \( \, 3 \, \) eller \( \, 4 \).

Alltså har ekvationen de två lösningarna:


\(\qquad\begin{align} x_1 & = 3 \\ x_2 & = 4 \end{align} \)

Nollproduktmetoden ger oss ekvationens lösningar utan att vi behöver räkna!

Den felaktiga åtgärden ovan är formellt matematiskt inte fel, men är ineffektiv och förstör faktorformen.

Faktorformen är den struktur som gör nollproduktmetoden och därmed den effektiva lösningen möjlig.


Ett polynom i faktorform visar sina nollställen istället för koefficienterna.

Men hur får man faktorformen om man har polynomet som en summa av termer? Man måste bestämma nollställena:


Faktorisering av 2:a gradspolynom (normalform)

Uppgiften: Faktorisera polynomet \( \, x^2 - 7\,x + 12 \).

Lösningen: Vi beräknar polynomets nollställen:

\[ x^2 - 7\,x + 12 = 0 \]

För att snabbt lösa denna 2:a gradsekvation som ett led i faktoriseringsprocessen

använder vi Vietas formler:

\[ \begin{align} x_1 + x_2 & = -p = -(-7) = 7 \\ x_1 \cdot x_2 & = \;\;\; q = 12 \end{align}\]

Dvs vi behöver hitta två tal vars produkt är \( \, 12 \, \) och vars summa är \( \, 7 \, \).

Med lite provande kommer man fram till:

\[\begin{align} x_1 & = 3 \\ x_2 & = 4 \end{align}\]

eftersom \( \, 3 + 4 = 7 \, \) och \( \, 3 \cdot 4 = 12 \). Därmed är polynomets faktorisering:

\[ x^2 - 7\,x + 12 \; = \; \underline{(x - 3) \, \cdot \, (x - 4)} \]


Självklart hade man kunnat använda även pq-formeln för att lösa 2:a gradsekvationen. Då hade det sett ut så här:

\[\begin{array}{rcl} x^2 - 7\,x + 12 & = & 0 \\ x_{1,2} & = & 3,5 \pm \sqrt{12,25 - 12} \\ x_{1,2} & = & 3,5 \pm \sqrt{0,25} \\ x_{1,2} & = & 3,5 \pm 0,5 \\ x_1 & = & 3 \\ x_2 & = & 4 \end{array}\]

Man ser att Vieta inte bara är en enklare och snabbare metod än pq-formeln utan även minimerar risken för felräkning.

Faktorformen (produkten) är resultat av faktorisering (processen). Exemplets polynom är av grad \( \, 2\), medan dess ingredienser dvs faktorerna \( \, (x-3) \, \) och \( \, (x-4) \, \) är polynom av grad \( \, 1\).

Detta kan jämföras med faktoriseringen \( \, 12 \, = \, 3 \cdot 4 \), där faktorerna \( \, 3 \, \) och \( \, 4 \, \) är mindre än \( \, 12 \, \). Man har splittrat upp talet \( \, 12 \,\) i sina beståndsdelar \( \, 3 \, \) och \( \, 4 \), precis som man

splittrar upp polynomet \( \, x^2 - 7\,x + 12 \, \) i sina beståndsdelar \( \, (x-3)\, \) och \( \, (x-4) \).

Faktorisering är relevant av olika skäl: För det första tillåter faktorformen förkortning och därmed förenkling av komplexa algebraiska uttryck. För det andra avslöjar faktorformen polynomets nollställen.

Det vi genomförde för vårt exempel kan generaliseras till alla 2:gradspolynom, åtminstone sådana som är givna i normalform:

Sats:

Faktorisering med 2 nollställen

Om 2:a gradspolynomet \( x^2 + p\,x + q \) har nollställena \( x_1\, \) och \( x_2\, \) så gäller:

\[ x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) \]

För att bevisa satsen ovan kan man t.ex.

Se beviset i lösningen till övning 13.

Det finns motsvarande satser om polynom av högre grad än 2, se Algebrans fundamentalsats.

Praktisk slutsats:

För att faktorisera ett 2:a gradspolynom i normalform måste vi beräkna dess

nollställen \( x_1\, \) och \( x_2\, \). Sedan blir faktoriseringen: \( \quad (x-x_1) \cdot (x-x_2) \)


Rotens olika betydelser

Ordet rot har i matematiken olika betydelser i olika sammanhang:

  1.    Räkneoperationen rotdragning med rottecknet \( {\color{White}{y=}}\!\!\!\!\!\!\!\!\sqrt{\color{White}x} \) som symbol, t.ex. roten ur \( 4\, \) är \( 2\, \) osv.
  2.    Lösningen av en ekvation. Rot är synonym till en ekvations lösning. T.ex. är \( x_1 = 2\, \) och \( x_2 = -2\, \) rötter dvs lösningar till ekvationen \( x^2 = 4\, \).
  3.    Nollstället till ett polynom. Rot är synonym till ett polynoms nollställe. I exemplet ovan är \( x_1 = 2\, \) och \( x_2 = -2\, \) rötter dvs nollställen till polynomet \( x^2 - 4\, \).

Sammanhanget avgör vilken betydelse som gäller just i den aktuella kontexten.


Dubbelrot

När vi nu i fortsättningen pratar om en dubbelrot menar vi två lösningar till en ekvation som sammanfaller, vilket även kan uppfattas som endast en lösning.

Sats:

Faktorisering med 1 nollställe

Om 2:gradspolynomet \( x^2 + p\,x + q \) endast har ett nollställe \( x_1\, \) så gäller:

\[ x^2 + p\,x + q = (x-x_1)^2 \]

Ett sådant nollställe kallas för dubbelrot till ekvationen \( x^2 + p\,x + q = 0 \).


Exempel

Polynomet \( x^2 - 6\,x + 9 \) har dubbelroten \( x = 3\, \) eftersom \( x^2 - 6\,x + 9 \, = \, (x-3)\,^2 \), se Enkel faktorisering av polynom.

Vi ritar grafen till polynomfunktionen och undersöker på vilket sätt kurvan "skär" \( \, x\)-axeln.

Grafen till polynomfunktionen \( \; y = x^2 - 6\,x + 9 \; {\rm :} \quad\quad \) 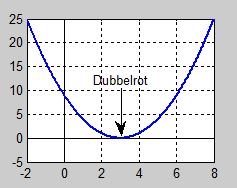Dubbelrot.jpg

Grafen visar att kurvan inte skär utan bara berör \(\,x\)-axeln vid \( x = 3\, \).

Dvs det finns endast en gemensam punkt mellan kurvan och \(\,x\)-axeln.

Dubbelrötter ligger på gränsen mellan att skära (två lösningar) och inte skära \(\,x\)-axeln (ingen lösning alls).

Matematiskt uttrycker sig detta i faktoriseringens form:

\[ x^2 - 6\,x + 9 = (x-3) \cdot (x-3) = (x-3)\,^2 \]

Det intressanta med dubelrötter är att vi endast har en lösning \( x = 3\, \) till 2:a gradsekvationen \( x^2 - 6 x + 9 = 0\, \). Fast, om vi tittar på faktorformen \( (x - 3) \cdot (x - 3) = 0 \) kan man lika bra säga

att vi har två identiska lösningar eller två som sammanfaller - ett filosofiskt dilemma som man matematiskt brukar lösa upp genom att kalla lösningen för en dubbelrot.

Andra viktiga egenskaper av dubbelrötter kommer vi att lära känna senare när vi i kapitel 2 behandlar derivering.


Internetlänkar

http://tutorial.math.lamar.edu/Classes/Alg/Factoring.aspx

http://mathworld.wolfram.com/PolynomialFactorization.html

http://www.mathsisfun.com/algebra/fundamental-theorem-algebra.html

http://www.sosmath.com/algebra/factor/fac04/fac04.html

http://www.lboro.ac.uk/research/helm/C_HELM_backup_24nov03/helm_website/documents/wb03_blk3.pdf





Copyright © 2019 TechPages AB. All Rights Reserved.

Hämtad från "https://matte3c.mathonline.se/index.php?title=1.2_Faktorisering_av_polynom&oldid=36850"