Skillnad mellan versioner av "1.6 Absolutbelopp"

Från Mathonline
Hoppa till: navigering, sök
m
m
 
(233 mellanliggande versioner av samma användare visas inte)
Rad 1: Rad 1:
 +
__NOTOC__
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
−
{{Not selected tab|[[1.5 Kontinuerliga och diskreta funktioner|<-- Förra avsnitt]]}}
+
{{Not selected tab|[[1.5 Kontinuerliga och diskreta funktioner| <<&nbsp;&nbsp;Förra avsnitt]]}}
 
{{Selected tab|[[1.6 Absolutbelopp|Genomgång]]}}
 
{{Selected tab|[[1.6 Absolutbelopp|Genomgång]]}}
 
{{Not selected tab|[[1.6 Övningar till Absolutbelopp|Övningar]]}}
 
{{Not selected tab|[[1.6 Övningar till Absolutbelopp|Övningar]]}}
Rad 8: Rad 9:
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
−
<div style= "border:1px solid white; display:inline-block !important; margin-left: 675px !important; padding:2px 8px 2px 2px;">
+
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
−
<table>
+
| style="border-bottom:1px solid #797979" width="5px" | &nbsp;
−
<tr>
+
{{Not selected tab|    }}
−
  <td>[[Lösningar till diagnosprov 1 i Matte 3 kap 1 Algebra och funktioner|<span style="color:blue">&nbsp;&nbsp;&nbsp;Lösningar&nbsp;till&nbsp;diagnosprov&nbsp;1&nbsp;kap&nbsp;1</span>]]</td>
+
{{Not selected tab|[[1.6 Fördjupning till Absolutbelopp|Fördjupning]]}}
−
  <td>[[Lösningar till diagnosprov 2 kap 1|<span style="color:blue">&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;Lösningar&nbsp;till&nbsp;diagnosprov&nbsp;2&nbsp;kap&nbsp;1</span>]]</td>
+
{{Not selected tab|    }}
−
</tr>
+
{{Not selected tab|[[Lösningar till diagnosprov 1 i Matte 3 kap 1 Algebra och funktioner|Lösningar Diagnos 1]]}}
−
</table>
+
{{Not selected tab|[[Lösningar till diagnosprov 2 kap 1|Lösningar&nbsp;Diagnos 2]]}}
−
</div>
+
| style="border-bottom:1px solid #797979" width="100%"| &nbsp;
−
[[Media: Lektion 9 Absolutbelopp Ruta.pdf|<strong><span style="color:blue">Lektion 10 Absolutbelopp</span></strong>]]
+
|}
−
__NOTOC__
+
 
 +
 
 +
<!-- [[Media: Lektion 11 Absolutbelopp Rutab.pdf|<b><span style="color:blue">Lektion 11 Absolutbelopp</span></b>]] -->
 
<big>
 
<big>
 +
<div class="ovnE">
 +
<small>
 +
=== <b><span style="color:#931136">Några exempel på absolutbelopp</span></b> ===
 +
<br>
 
<div class="exempel">
 
<div class="exempel">
−
=== <b><span style="color:#931136">Exempel 1 Åldersskillnad</span></b> ===
+
==== <b><span style="color:#931136">Exempel 1 &nbsp;&nbsp; Åldersskillnad</span></b> ====
  
−
En dejtingsajt på nätet har bestämt sig för policyn att åldersskillnaden mellan två partner ska vara mindre än <math> 6 \, </math> år.
+
En dejtingsajt på nätet har bestämt sig för att åldersskillnaden mellan två partner ska vara <b><span style="color:red"><math> \, < \, 6 \, </math> år</span></b>.
  
−
För att beräkna åldersskillnaden i sina webbformulär använder de följande formel som ger utskrifterna till höger efter att några kunder skickat in sina uppgifter:
+
I sina webbformulär använder de följande formel som ger utskrifterna till höger
 +
 
 +
efter att några kunder skickat in sina uppgifter:
  
 
<table>
 
<table>
Rad 34: Rad 43:
 
-webkit-border-radius: 10px;
 
-webkit-border-radius: 10px;
 
-moz-border-radius: 5px;
 
-moz-border-radius: 5px;
−
border-radius: 5px;"><strong><math> \mbox{Age}_\mbox{male} - \mbox{Age }_\mbox{female}\, </math></strong></div></td>
+
border-radius: 5px;"><b><math> \mbox{Age}_\mbox{male} - \mbox{Age }_\mbox{female}\, </math></b></div></td>
−
   <td><math> \qquad\qquad\qquad </math></td>
+
   <td><math> \qquad\qquad </math></td>
 
   <td><math> 25 \quad - \quad 20 \quad = \quad 5 </math>
 
   <td><math> 25 \quad - \quad 20 \quad = \quad 5 </math>
  
−
<math> 30 \quad - \quad 23 \quad = \quad 7 </math>
+
<math> 26 \quad - \quad 22 \quad = \quad 4 </math>
  
−
<math> 22 \quad - \quad 26 \quad = \quad \boxed{-4} </math></td>
+
<math> 23 \quad - \quad 30 \quad = \quad {\color{Red} {\boxed{-7}}} </math></td>
 +
  <td><math> \quad </math></td>
 +
  <td><math> < \; 6 \quad \Rightarrow \quad {\rm ok} </math>
 +
 
 +
<math> < \; 6 \quad \Rightarrow \quad {\rm ok} </math>
 +
 
 +
<math> < \; 6 \quad \Rightarrow \quad {\rm {\color{Red} {\bf{ok}}}} </math></td>
 
</tr>
 
</tr>
 
</table>
 
</table>
  
−
Lovisa som sommarjobbar på dejtingsajten blir konfunderad över den sista utskriften som är negativ, och undrar om åldersskillnad kan vara negativ.
+
Lovisa som sommarjobbar på dejtingsajten konstaterar att den sista utskriften ger <b><span style="color:red">fel</span></b> resultat: Åldersskillnaden är <b><span style="color:red"><math> \, > \, 6 \, </math> år</span></b>.
  
−
Faktiskt är det meningslöst att ange åldersskillnaden med ett negativt tal. Åldersskillnad måste alltid vara positiv för att vara meningsfull.
+
Felet beror på att <b><span style="color:red">negativ</span></b> åldersskillnad inte är meningsfull. Åldersskillnad måste alltid vara <b><span style="color:red">positiv</span></b>.
  
−
Lovisa som lärt sig <strong><span style="color:red">absolutbelopp</span></strong> på Matte 3-kursen föreslår att man ändrar formeln. Efter ändringen blir det så här:
+
Lovisa som lärt sig <b><span style="color:red">absolutbelopp</span></b> på Matte 3-kursen föreslår att man ändrar formeln. Efter ändringen blir det så här:
  
 
<table>
 
<table>
Rad 58: Rad 73:
 
-webkit-border-radius: 10px;
 
-webkit-border-radius: 10px;
 
-moz-border-radius: 5px;
 
-moz-border-radius: 5px;
−
border-radius: 5px;"><strong><math> { \color{Red} |} \, \mbox{Age}_\mbox{male} - \mbox{Age }_\mbox{female} \, { \color{Red} |} </math></strong></div></td>
+
border-radius: 5px;"><b><math> { \color{Red} |} \, \mbox{Age}_\mbox{male} - \mbox{Age }_\mbox{female} \, { \color{Red} |} </math></b></div></td>
−
   <td><math> \qquad\qquad </math></td>
+
   <td><math> \qquad\quad </math></td>
 
   <td><math> { \color{Red} |} \, 25 \quad - \quad 20 \, { \color{Red} |} \quad = \quad 5 </math>
 
   <td><math> { \color{Red} |} \, 25 \quad - \quad 20 \, { \color{Red} |} \quad = \quad 5 </math>
  
−
<math> { \color{Red} |} \, 30 \quad - \quad 23 \, { \color{Red} |} \quad = \quad 7 </math>
+
<math> { \color{Red} |} \, 26 \quad - \quad 22 \, { \color{Red} |} \quad = \quad 4 </math>
  
−
<math> { \color{Red} |} \, 22 \quad - \quad 26 \, { \color{Red} |} \quad = \quad \boxed{4} </math></td>
+
<math> { \color{Red} |} \, 23 \quad - \quad 30 \, { \color{Red} |} \quad = \quad {\color{Red} {\boxed{7}}} </math></td>
 +
  <td><math> \quad </math></td>
 +
  <td><math> < \; 6 \quad \Rightarrow \quad {\rm ok} </math>
 +
 
 +
<math> < \; 6 \quad \Rightarrow \quad {\rm ok} </math>
 +
 
 +
<math> {\color{Red} {\bf{>}}} \,\; 6 \quad \Rightarrow \quad {\rm {\color{Red} {\bf{inte\;ok}}}} </math></td>
 
</tr>
 
</tr>
 
</table>
 
</table>
  
−
Nu känns det ok. Ändringen i den sista utskriften beror på följande:
+
Nu stämmer det, vilket beror på att Lovisa infogade de två raka strecken <math> \; {\color{Red} |} \, \quad \, {\color{Red} |} \; </math> i formeln, vilket korrigerade den sista utskriften:
  
−
::<math> { \color{Red} |} \, 22 \quad - \quad 26 \, { \color{Red} |} \quad = \quad { \color{Red} |} \, - 4 \, { \color{Red} |} \quad = \quad 4 </math>
+
::<math> { \color{Red} |} \, 23 \quad - \quad 30 \, { \color{Red} |} \quad = \quad { \color{Red} |} \, - 7 \, { \color{Red} |} \quad = \quad 7 </math>
  
−
<math> \; {\color{Red} |} \, \quad \, {\color{Red} |} \; </math> tar bort minustecknet från <math> -4\, </math> och returnerar <math> 4\, </math>. Därför<span style="color:black">:</span> <math> { \color{Red} |} \, - 4 \, { \color{Red} |} = 4 </math>.  
+
<math> \; {\color{Red} |} \, \quad \, {\color{Red} |} \; </math> tar bort minustecknet från <math> -7\, </math> och ger <math> 7\, </math>. Därför<span style="color:black">:</span> <math> { \color{Red} |} \, - 7 \, { \color{Red} |} = 7 </math>.  
 
</div>
 
</div>
  
  
  
−
De två raka strecken <math> \; {\color{Red} |} \, \quad \, {\color{Red} |} \; </math> som skrivs kring ett värde eller ett uttryck, kallas för <strong><span style="color:red">absolutbelopp</span></strong> och betyder:
+
<div class="border-divblue">
 +
De två raka strecken <math> \; {\color{Red} |} \, \quad \, {\color{Red} |} \; </math> som skrivs kring ett tal eller ett uttryck, kallas för <b><span style="color:red">absolutbelopp</span></b> och&nbsp;betyder:
  
−
<strong><span style="color:red">Att göra om ett negativt tal till ett positivt tal och låta ett positivt tal vara oförändrat.</span></strong>&nbsp;&nbsp;&nbsp;&nbsp;
+
::<b><span style="color:red">Att göra om ett negativt tal till ett positivt tal och låta ett positivt tal vara oförändrat.</span></b>&nbsp;&nbsp;&nbsp;&nbsp;
  
−
 
+
Kortare: &nbsp;&nbsp; Ett tals absolutbelopp är talets <b>positiva värde</b>, t.ex.:
−
<div class="border-divblue">
+
−
Ett tals absolutbelopp är talets positiva värde.
+
 
</div>
 
</div>
−
 
−
 
−
<div class="exempel"> <!-- exempel -->
 
−
=== <b><span style="color:#931136">Exempel på absolutbelopp</span></b> ===
 
 
<table>
 
<table>
−
<tr>
+
<tr><td>
−
<td>
+
::<math> | \, - 7 \, | \, = \, 7 </math>
−
:::<math> | \, - 7 \, | \, = \, 7 </math>
+
  
−
:::<math> | \, - 0,5 \, | \, = \, 0,5 </math>
+
::<math> | \, - 0,5 \, | \, = \, 0,5 </math>
  
−
:::<math> \left| \, - \sqrt{5} \, \right| \, = \, \sqrt{5} </math>
+
::<math> \left| \, - \sqrt{5} \, \right| \, = \, \sqrt{5} </math>
 
</td>
 
</td>
 +
<td><math> \qquad\quad </math></td>
 
<td>
 
<td>
 
::::<math> | \; 23 \; | \, = \, 23 </math>
 
::::<math> | \; 23 \; | \, = \, 23 </math>
Rad 105: Rad 121:
 
::::<math> \left| \, 0 \, \right| \, = \, 0 </math>
 
::::<math> \left| \, 0 \, \right| \, = \, 0 </math>
 
</td>
 
</td>
 +
<td><math> \qquad\quad </math></td>
 
<td>
 
<td>
 
::::<math> \displaystyle{ \left| \, {13\over 4} \, \right| \, = \, {13\over 4} } </math>
 
::::<math> \displaystyle{ \left| \, {13\over 4} \, \right| \, = \, {13\over 4} } </math>
Rad 112: Rad 129:
 
::::<math> \left| \, \sqrt{3} \, \right| \, = \, \sqrt{3} </math>
 
::::<math> \left| \, \sqrt{3} \, \right| \, = \, \sqrt{3} </math>
 
</td>
 
</td>
 +
<td><math> \qquad\quad </math></td>
 
<td>
 
<td>
−
::::<math> | \, i \, | \, = \, 1  </math>
+
::::<math> | \, a \, - \, b \, | \, = \, | \, b \, - \, a \, | </math> (se <small><b><span style="color:#931136">Exempel 2</span></b></small>)
  
−
::::<math> | \, a \, - \, b \, | \, = \, | \, b \, - \, a \, | </math>
+
::::<math> | \, i \, | \, = \, | \, \sqrt{-1} \, | \, = \, 1  </math> (se <small><b><span style="color:#931136">Exempel 3</span></b></small>)
−
</td>
+
</td></tr>
−
</tr>
+
 
</table>
 
</table>
−
</div> <!-- exempel -->
+
<div class="border-divblue">
 +
Absolutbelopp lämpar sig för att modellera storheter som till sin natur är <b>positiva</b> som t.ex. åldersskillnad.
  
 +
Andra exempel är avstånd, längd, area, volym, massa (vikt), tid, lufttryck, vindstyrka, pengar, antal objekt, <math> \, \ldots \; </math>.
 +
</div>
  
−
Om talet är negativt tar absolutbeloppet bort bara minustecknet och returnerar talets positiva värde. Men om talet är positivt eller <math> 0\, </math> gör absolutbeloppet ingenting.
+
Vi tittar närmare på avstånd:
−
 
+
−
Därför lämpar sig absolutbeloppet för att modellera storheter som av sin natur är positiva, som t.ex. åldersskillnaden. Ett annat exempel är avståndet.
+
−
 
+
  
 
<div class="exempel">
 
<div class="exempel">
−
=== <b><span style="color:#931136">Exempel 2 Avstånd mellan två tal</span></b> ===
+
==== <b><span style="color:#931136">Exempel 2 &nbsp;&nbsp; Avstånd mellan två tal</span></b> ====
  
−
Vad är avståndet mellan <math> \, 2 \, </math> och <math> \, 5 \, </math>? Svar<span style="color:black">:</span> <math> \quad 5 \, - \, 2 \, = \, 3 </math>
+
Vad är avståndet mellan <math> \, 2 \, </math> och <math> \, 5 \, </math>? &nbsp;&nbsp; Svar<span style="color:black">:</span> <math> \quad 5 \, - \, 2 \, = \, 3 </math>
  
 
Vad är då avståndet mellan <math> -2 \, </math> och <math> -5 \, </math>? Gör man samma sak blir svaret<span style="color:black">:</span> <math> \quad -5 \, - \, (-2) \, = \, -5 \, + \, 2 \, = \, -3 </math>
 
Vad är då avståndet mellan <math> -2 \, </math> och <math> -5 \, </math>? Gör man samma sak blir svaret<span style="color:black">:</span> <math> \quad -5 \, - \, (-2) \, = \, -5 \, + \, 2 \, = \, -3 </math>
  
−
Men vi vet att avståndet mellan <math> -2 \, </math> och <math> -5 \, </math> är <math> 3 \, </math> och inte <math> -3 \, </math>. Ett avstånd kan inte vara negativt. Avstånd är alltid positivt, precis som åldersskillnad.
+
Men vi vet att avståndet mellan <math> -2 \, </math> och <math> -5 \, </math> är <math> 3 \, </math> och inte <math> -3 \, </math>. Ett avstånd kan inte vara negativt. Avstånd är alltid positivt.
  
−
Korrekt svar<span style="color:black">:</span> <math> \quad {\color{Red} |} \, -5 - (-2) \, { \color{Red} |} \; = \; { \color{Red} |} -5 + 2 \, { \color{Red} |} \, = \, { \color{Red} |} -3 \, { \color{Red} |} \; = \; 3 </math>
+
Korrekt svar<span style="color:black">:</span>
 +
 
 +
:::<math> {\color{Red} |} \, -5 - (-2) \, { \color{Red} |} \; = \; { \color{Red} |} -5 + 2 \, { \color{Red} |} \, = \, { \color{Red} |} -3 \, { \color{Red} |} \; = \; 3 </math>
  
 
Fortfarande dras talen av från varandra, men absolutbelopp kring subtraktionen gör att resultatet blir positivt.
 
Fortfarande dras talen av från varandra, men absolutbelopp kring subtraktionen gör att resultatet blir positivt.
−
</div>
 
  
 +
Kastar vi om talens ordning blir det samma resultat<span style="color:black">:</span>
  
−
Nu kan vi beskriva avståndet mellan två tal med hjälp av absolutbeloppet:
+
:::<math> { \color{Red} |} \, -2 - (-5) \, { \color{Red} |} \; = \; { \color{Red} |} -2 + 5 \, { \color{Red} |} \, = \, { \color{Red} |} \, 3 \, { \color{Red} |} \; = \; 3 </math>
 +
</div>
 +
 
 +
Generellt gäller:
  
 
<div class="border-divblue">
 
<div class="border-divblue">
−
Avståndet mellan talen <math> \, a \, </math> och <math> \, b \, </math> är <math> \; | \, a - b \, | \; </math> eller <math> \; | \, b - a \, | \; </math>.
+
Absolutbeloppet <math> \; | \, a - b \, | \; </math> är avståndet mellan talen <math> \, a \, </math> och <math> \, b \, </math>.
 
</div>  
 
</div>  
  
 +
Det är irrelevant i vilken ordning talen skrivs. Det gäller<span style="color:black">:</span> <math> \quad | \, a - b \, | \, = \, | \, -(b - a) \, | \, = \, | \, b - a \, | </math>
  
−
Det är irrelevant i vilken ordning talen skrivs. Det gäller nämligen generellt<span style="color:black">:</span> <math> \quad | \, a - b \, | \, = \, | \, b - a \, | </math>
 
  
−
Kastar vi om talens ordning i Exempel 2 blir det samma resultat:
+
Ett specialfall av avståndet mellan två tal är, när det ena talet är <math> \, 0 \, </math>:
−
 
+
−
::<math> { \color{Red} |} \, -2 - (-5) \, { \color{Red} |} \; = \; { \color{Red} |} -2 + 5 \, { \color{Red} |} \, = \, { \color{Red} |} \, 3 \, { \color{Red} |} \; = \; 3 </math>
+
  
 
<div class="exempel">
 
<div class="exempel">
−
==== <b><span style="color:#931136">Avstånd från <math> \, 0 \, </math></span></b> ====
+
==== <b><span style="color:#931136">Exempel 3 &nbsp;&nbsp; Avstånd från <math> \, 0 \, </math></span></b> ====
  
−
Om vi i den nya definitionen för avstånd <math> | \, a - b \, | \, </math> sätter in <math> a = 0 \, </math> och <math> b = -5 \, </math> för att beräkna avståndet mellan <math> 0 \, </math> och <math> -5 \, </math> får vi:
+
Om vi i den nya definitionen för avstånd <math> \, | \, a - b \, | \, </math> sätter in <math> a = 0 \, </math> och <math> b = -5 \, </math> för att beräkna avståndet mellan <math> 0 \, </math> och <math> -5 \, </math> får vi:
  
−
::<math> | \, 0 - (-5) \, | \, = \, | \, 0 + 5 \, | \, = \, | \, 5 \, | \, = \, 5 </math>  
+
:::<math> | \, 0 - (-5) \, | \, = \, | \, 0 + 5 \, | \, = \, | \, 5 \, | \, = \, 5 </math>  
  
−
Om vi kastar om ordningen blir det samma resultat:  
+
Och tar vi <math> \, | \, b - a \, | \, </math> blir det samma resultat:  
  
−
::<math> | -5 - 0 \, | \, = \, | -5 \, | \, = \, 5 </math>
+
:::<math> | -5 - 0 \, | \, = \, | -5 \, | \, = \, 5 </math>
  
 
<math> 5 \, </math> är alltså talet <math> \, -5</math>:s avstånd från <math> 0 \, </math>.
 
<math> 5 \, </math> är alltså talet <math> \, -5</math>:s avstånd från <math> 0 \, </math>.
 
</div>
 
</div>
  
−
 
+
Detta ger oss en ny tolkning av absolutbeloppet som gäller för alla tal, även för komplexa (se exemplet <math> | \, i \, | = 1 </math> ovan och motivera!):
−
Detta gäller för alla tal, vilket ger oss en ny tolkning av absolutbeloppet:
+
  
 
<div class="border-divblue">
 
<div class="border-divblue">
−
Ett tals absolutbelopp är talets avstånd från 0.
+
Absolutbeloppet <math> \; | \, a \, | \; </math> är talet <math> a</math>:s avstånd från 0.  
 
</div>  
 
</div>  
  
 +
</small>
 +
</div> <!-- "ovnE" -->
  
−
Alla hittills nämnda tolkningar av absolutbeloppet är utmärkta att använda i många sammanhang och ger oss en bra intuitiv uppfattning av begreppet. Men de är inga strikt matematiska definitioner och lämpar sig inte t.ex. för att lösa ekvationer eller olikheter som involverar absolutbelopp. Därför:
 
  
 +
Alla hittills nämnda tolkningar av absolutbeloppet är utmärkta att använda i många sammanhang och ger oss en bra intuitiv uppfattning av begreppet.
  
−
<div class="ovnE">  
+
Men de är inga strikt matematiska definitioner och lämpar sig inte t.ex. för att lösa ekvationer eller olikheter som involverar absolutbelopp. Därför:
 +
 
 +
 
 +
<div class="ovnC">  
 
<small>
 
<small>
−
=== <b><span style="color:#931136">Allmän definition och graf</span></b> ===
+
=== <b><span style="color:#931136">Allmän definition, funktion och graf</span></b> ===
 +
<div class="border-divblue">
 
<table>
 
<table>
 
<tr>
 
<tr>
 
   <td>Absolutbeloppet <math> \; | \, x \, | \; </math> av ett tal <math> x\, </math> definieras genom<span style="color:black">:</span>
 
   <td>Absolutbeloppet <math> \; | \, x \, | \; </math> av ett tal <math> x\, </math> definieras genom<span style="color:black">:</span>
  
−
 
+
::::<math> | \, x \, | \, = \, \begin{cases} \;\, x & \mbox{om } x  \geq  0  \\
−
 
+
                                              -x & \mbox{om } x  <  0    \\
−
::<math> | \, x \, | \, = \, \begin{cases} \;\, x & \mbox{om } x  \geq  0  \\
+
−
                                                    -x & \mbox{om } x  <  0    \\
+
 
\end{cases}
 
\end{cases}
 
</math>
 
</math>
  
−
 
+
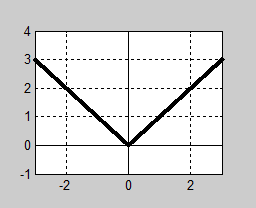
Grafen till &nbsp; <b><span style="color:#931136">funktionen <math> \; y = | \, x \, | \; </math></span></b> ser ut så här:
−
 
+
−
Grafen till funktionen <math> \; y = | \, x \, | \; </math> ser ut så här:
+
−
 
+
−
 
+
 
</td>
 
</td>
 
   <td><math> \qquad </math></td>
 
   <td><math> \qquad </math></td>
Rad 204: Rad 223:
 
</tr>
 
</tr>
 
</table>
 
</table>
 +
Absolutbeloppet är en funktion som är definierad och kontinuerlig för alla <math> x \, </math>.
 +
</div>
 +
</small>
 +
</div>
  
−
Absolutbeloppet är en funktion som är definierad för alla <math> x \, </math>. Den är även kontinuerlig för alla <math> x \, </math>.
+
−
 
+
<div class="ovnC">
−
<b>OBS!</b> &nbsp; I följande exempel ska absolutbelopp bestämmas genom att använda den allmänna definitionen ovan, inte intuitivt.
+
<small>
−
<!-- I förra avsnittets  [[1.5_Övningar_till_Kontinuerliga_och_diskreta_funktioner#.C3.96vning_8|<strong><span style="color:blue">övn 8</span></strong>]] hade vi redan stiftat bekantskap med den utan att nämna dess namn. -->
+
<b>OBS!</b> &nbsp; I följande exempel ska absolutbelopp bestämmas genom att använda den allmänna definitionen, inte intuitivt.
 +
<!-- I förra avsnittets  [[1.5_Övningar_till_Kontinuerliga_och_diskreta_funktioner#.C3.96vning_8|<b><span style="color:blue">övn 8</span></b>]] hade vi redan stiftat bekantskap med den utan att nämna dess namn. -->
  
 
<div class="exempel">
 
<div class="exempel">
−
<strong><span style="color:#931136">Exempel 1:</span></strong>
+
<b><span style="color:#931136">Exempel 1:</span></b>
  
 
::Vad är <math> | \, 7 \, | </math> enligt definitionen ovan?  
 
::Vad är <math> | \, 7 \, | </math> enligt definitionen ovan?  
  
−
::Eftersom <math> x = 7 \geq 0 </math> väljs det första alternativet (första raden) i definitionen efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> x = 7\, </math>.  
+
::Eftersom <math> x = 7 \geq 0 </math> väljs det första alternativet (första raden) i definitionen efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> | \, 7 \, | = 7\, </math>.  
  
 
::<b>Svar:</b> <math> \; | \, 7 \, | = 7 </math>.
 
::<b>Svar:</b> <math> \; | \, 7 \, | = 7 </math>.
Rad 222: Rad 246:
  
 
<div class="exempel">
 
<div class="exempel">
−
<strong><span style="color:#931136">Exempel 2:</span></strong>
+
<b><span style="color:#931136">Exempel 2:</span></b>
  
 
::Vad är <math> | \, - 5 \, | </math> enligt definitionen ovan?
 
::Vad är <math> | \, - 5 \, | </math> enligt definitionen ovan?
  
−
::Eftersom <math> x = -5 < 0\, </math> väljs det andra alternativet (andra raden) i definitionen efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> -x = -(-5)\, </math> vilket ger <math> 5\, </math>.
+
::Eftersom <math> x = -5 < 0\, </math> väljs det andra alternativet (andra raden) i definitionen efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> | \, - 5 \, | \, = \, -(-5) \, = \, 5 </math>.
  
 
::<b>Svar:</b> <math> \; | \, - 5 \, | = 5 </math>.
 
::<b>Svar:</b> <math> \; | \, - 5 \, | = 5 </math>.
Rad 233: Rad 257:
  
 
<div class="exempel">
 
<div class="exempel">
−
<strong><span style="color:#931136">Exempel 3:</span></strong>
+
<b><span style="color:#931136">Exempel 3:</span></b>
  
 
::Vad är <math> | \, 0 \, | </math> enligt definitionen ovan?  
 
::Vad är <math> | \, 0 \, | </math> enligt definitionen ovan?  
  
−
::Eftersom <math> x = 0 \geq 0 </math> väljs det första alternativet (första raden) i definitionen efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> x = 0\, </math>.  
+
::Eftersom <math> x = 0 \geq 0 </math> väljs det första alternativet (första raden) i definitionen efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> | \, 0 \, | = 0\, </math>.  
  
 
::<b>Svar:</b> <math> \; | \, 0 \, | = 0 </math>.
 
::<b>Svar:</b> <math> \; | \, 0 \, | = 0 </math>.
Rad 244: Rad 268:
  
 
<div class="exempel">
 
<div class="exempel">
−
<strong><span style="color:#931136">Exempel 4:</span></strong>
+
<b><span style="color:#931136">Exempel 4:</span></b>
  
 
::Vad är <math> | \, a + 2 \, | </math> enligt definitionen ovan?  
 
::Vad är <math> | \, a + 2 \, | </math> enligt definitionen ovan?  
Rad 250: Rad 274:
 
::Eftersom vi inte känner till <math> \, a</math>:s värde och därför inte vet om <math> \, a + 2 </math> blir positivt eller negativt, måste vi skilja mellan två fall:  
 
::Eftersom vi inte känner till <math> \, a</math>:s värde och därför inte vet om <math> \, a + 2 </math> blir positivt eller negativt, måste vi skilja mellan två fall:  
  
−
::<u><b>Fall 1</b></u> <math> \; a + 2 \geq 0 \quad \; </math> eller <math> \;\quad a \geq -2 </math>
+
::<u><b>Fall 1</b></u> <math> \quad a + 2 \geq 0 \quad \; </math> eller <math> \;\quad a \geq -2 </math>
  
−
::Eftersom <math> x = a + 2 \geq 0 </math> väljs det första alternativet (första raden) i definitionen efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> x = a + 2\, </math>.  
+
::Eftersom <math> x = a + 2 \geq 0 </math> väljs det första alternativet (första raden) i definitionen efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> | \, a + 2 \, | = a + 2\, </math>.  
  
−
::<u><b>Fall 2</b></u> <math> \; a + 2 < 0 \quad \; </math> eller <math> \;\quad a < -2 </math>
+
::<u><b>Fall 2</b></u> <math> \quad a + 2 < 0 \quad \; </math> eller <math> \;\quad a < -2 </math>
  
−
::Eftersom <math> \; x = a + 2 < 0\, </math> väljs det andra alternativet (andra raden) i definitionen efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> -x = -(a + 2)\, </math> vilket ger <math> -a - 2\, </math>.  
+
::Eftersom <math> \; x = a + 2 < 0\, </math> väljs det andra alternativet (andra raden) i definitionen efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> | \, a + 2 \, | \, = \, -(a + 2) \, = \, -a - 2\, </math>.  
  
 
::<b>Svar:</b> <math> \; | \, a + 2 \, | \, = \, \begin{cases} \;\, a + 2 & \mbox{om } a \geq -2 \\
 
::<b>Svar:</b> <math> \; | \, a + 2 \, | \, = \, \begin{cases} \;\, a + 2 & \mbox{om } a \geq -2 \\
Rad 265: Rad 289:
  
 
</small>
 
</small>
−
</div> <!-- "ovnE" -->
+
</div> <!-- "ovnC" -->
  
  
Rad 275: Rad 299:
 
<br>
 
<br>
  
 +
<div class="ovnC">
 +
<small>
 
<div class="ovnE">
 
<div class="ovnE">
−
Lös ekvationen <math> \; \, | \, x + 1 \, | \, = \, 3 \, </math>.
+
Lös ekvationen <math> \; \, | \, x + 1 \, | \, = \, 3 </math>
 
</div>
 
</div>
  
  
−
:<big><b>Lösning:</b></big>
+
Eftersom vi inte känner till <math> \, x \, </math> måste vi skilja mellan två fall, när vi tillämpar absolutbeloppets definition:  
  
−
::Eftersom vi inte känner till <math> \, x</math> måste vi skilja mellan två fall:
+
<u><b>Fall 1</b></u> <math> \quad x + 1 \geq 0 \quad \; </math> eller <math> \;\quad x \geq -1 </math>
  
−
::<u><b>Fall 1</b></u> <math> \; x + 1 \geq 0 \quad \; </math> eller <math> \;\quad x \geq -1 </math>
+
Enligt absolutbeloppets definition väljs det första alternativet efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> | \, x + 1 \, | </math> blir <math> x + 1\, </math>.
  
−
::Enligt absolutbeloppets definition väljs det första alternativet efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> | \, x + 1 \, | </math> blir <math> x + 1\, </math>. Dvs i det här fallet kan vi ta bort absolutbeloppstecknen utan åtgärd. Ekvationen blir:
+
Dvs i det här fallet kan vi ta bort absolutbeloppstecknen utan åtgärd. Ekvationen blir:
  
−
::::<math>\begin{align}  x + 1 & = 3    \\
+
::<math>\begin{align}  x + 1 & = 3    \\
 
                         x    & = 3 - 1 \\
 
                         x    & = 3 - 1 \\
 
                         x_1  & = 2  
 
                         x_1  & = 2  
 
     \end{align}</math>
 
     \end{align}</math>
  
−
::Vi kollar om lösningen inte står i motsats till förutsättningen vi gjorde i <b>Fall 1</b>, nämligen <math> x \geq -1 </math>. Men faktiskt är <math> 2 \geq -1 </math>. Därmed kan vi godta denna lösning. Annars hade den varit en falsk rot.
+
Vi kollar om lösningen inte står i motsats till förutsättningen vi gjorde i <b>Fall 1</b>, nämligen <math> \, x \geq -1 </math>.
 +
 
 +
Men faktiskt är <math> 2 \geq -1 </math>. Därmed kan vi godta denna lösning.
 +
 
 +
Annars hade den varit en s.k. falsk rot, dvs en beräknad "rot" som inte uppfyller ekvationen, se [[1.6_Fördjupning_till_Absolutbelopp#Falska_r.C3.B6tter|<b><span style="color:blue">Falska rötter</span></b>]].
 +
 
 +
<b><span style="color:red">I ekvationer med absolutbelopp är sådana kontroller kring falska rötter obligatoriska.</span></b>
  
−
::I ekvationer med absolutbelopp är sådana kontroller obligatoriska. I nästa uppgift (se nedan) förekommer faktiskt en falsk rot.
+
<u><b>Fall 2</b></u> <math> \quad x + 1 < 0 \quad \; </math> eller <math> \;\quad x < -1 </math>
  
−
::<u><b>Fall 2</b></u> <math> \; x + 1 < 0 \quad \; </math> eller <math> \;\quad x < -1 </math>
+
Enligt absolutbeloppets definition väljs det andra alternativet efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> | \, x + 1 \, | </math> blir <math> -(x + 1) = -x - 1\, </math>.
  
−
::Enligt absolutbeloppets definition väljs det andra alternativet efter klammern <math> \begin{cases} \end{cases} </math>, dvs <math> | \, x + 1 \, | </math> blir <math> -(x + 1) = -x - 1\, </math>. Dvs i det här fallet måste vi ersätta <math> x + 1\, </math> med <math> -x - 1\, </math>, när vi tar bort absolutbeloppstecknen. Ekvationen blir:
+
Dvs i det här fallet måste vi ersätta <math> x + 1\, </math> med <math> -x - 1\, </math>, när vi tar bort absolutbeloppstecknen. Ekvationen blir:
  
−
::::<math>\begin{align}  -x - 1 & = 3  \\
+
::<math>\begin{align}  -x - 1 & = 3  \\
 
                       -3 - 1 & = x  \\
 
                       -3 - 1 & = x  \\
 
                           -4 & = x  \\
 
                           -4 & = x  \\
Rad 307: Rad 339:
 
     \end{align}</math>
 
     \end{align}</math>
  
−
::Även här måste vi kolla om lösningen är förenlig med förutsättningen vi gjorde i <b>Fall 2</b>, nämligen <math> x < -1\, </math>. Men faktiskt är <math> -4 < -1\, </math>. Därmed kan vi godta även denna lösning. Ekvationen har två lösningar.
+
Även här måste vi kolla om lösningen är förenlig med förutsättningen vi gjorde i <b>Fall 2</b>, nämligen <math> \, x < -1\, </math>.
  
−
::<b>Svar:</b> <math>\begin{align} \; \, \;
+
Men faktiskt är <math> -4 < -1\, </math>. Därmed kan vi godta även denna lösning. Ekvationen har två lösningar.
−
                        x_1 & = 2   \\
+
 
−
                        x_2 & = -4
+
<b>Svar:</b> <div class="ovnE"><math> x_1 = 2 \quad {\rm och} \quad x_2 = -4 </math></div>
−
        \end{align}</math>  
+
</small>
 +
</div> <!-- "ovnC" -->
 +
 
 +
<b>Ekvationens och lösningarnas grafiska tolkning:</b>
  
−
::Vi ritar i samma koordinatsystem.graferna till de två funktionerna:
+
Vi ritar i samma koordinatsystem graferna till de två funktioner som står i ekvationens resp. led:
 
<table>
 
<table>
 
<tr>
 
<tr>
Rad 325: Rad 360:
 
</tr>
 
</tr>
 
</table>
 
</table>
−
::Graferna bekräftar att det finns två lösningar. Även grafernas skärningspunkter <math> x_1 = 2\, </math> och <math> x_2 = -4\, </math> bekräftar de lösningar vi fått för ekvationen <math> \; | \, x + 1 \, | \, = \, 3 \; </math>.
+
Likheten mellan leden<span style="color:black">:</span> <math> \, | \, x + 1 \, | \, = \, 3 \, </math> innebär att ekvationens lösningar är skärningspunkternas <math> \, x</math>-koordinater.
−
 
+
−
 
+
−
----
+
−
 
+
−
 
+
−
<div class="ovnE">
+
−
Lös ekvationen <math> \; \, | \, x - 3 \, | - 2\,x\, = \, 1 \, </math>.
+
−
</div>
+
−
 
+
−
 
+
−
:<big><b>Lösning:</b></big>
+
−
 
+
−
::<u><b>Fall 1</b></u> <math> \; x - 3 \geq 0 \quad \; </math> eller <math> \;\quad x \geq 3 </math>
+
−
 
+
−
::Enligt absolutbeloppets definition blir i så fall <math> | \, x - 3 \, | = x - 3\, </math> och ekvationen blir:
+
−
 
+
−
::::<math>\begin{align}  x - 3 - 2\,x & = 1  \\
+
−
                            -\,x - 3 & = 1  \\
+
−
                              - 3 - 1 & = x  \\
+
−
                                  - 4 & = x  \\
+
−
                                x_1  & = - 4
+
−
    \end{align}</math>
+
−
 
+
−
::Vi kollar om lösningen inte står i motsats till förutsättningen vi gjorde i <b>Fall 1</b>, nämligen <math> x \geq 3 </math>. Faktiskt är <math> - 4 \not\ge 3 </math>. Därmed måste vi <strong><span style="color:red">förkasta</span></strong> denna lösning. <math> x_1  = - 4\, </math> är en <strong><span style="color:red">falsk rot</span></strong>.
+
−
 
+
−
::<u><b>Fall 2</b></u> <math> \; x - 3 < 0 \quad \; </math> eller <math> \;\quad x < 3 </math>
+
−
 
+
−
::Enligt absolutbeloppets definition blir i så fall <math> | \, x - 3 \, | = -(x - 3) = -x + 3\, </math> och ekvationen blir:
+
−
 
+
−
::::<math>\begin{align}  -\,x + 3 - 2\,x & = 1     \\
+
−
                            -\,3\,x + 3 & = 1    \\
+
−
                                  3 - 1 & = 3\,x  \\
+
−
                                      2 & = 3\,x  \\
+
−
                            {2 \over 3} & = x   
+
−
          \end{align}</math> 
+
−
 
+
−
::Även här måste vi kolla om lösningen är förenlig med förutsättningen vi gjorde i <b>Fall 2</b>, nämligen <math> x < 3\, </math>. Det stämmer att <big><math> {2 \over 3} </math></big> <math> < 3 </math>. Därmed kan vi godta även denna lösning. Ekvationen har endast denna lösning.
+
−
 
+
−
::<b>Svar:</b> <math>\begin{align} \; \, \;
+
−
                        x & = {2 \over 3} 
+
−
        \end{align}</math>
+
−
 
+
−
::Vi ritar i samma koordinatsystem graferna till de två funktionerna:
+
−
<table>
+
−
<tr>
+
−
  <td><math> \qquad\qquad \begin{align}  y_1 & = | \, x - 3 \, |  \\
+
−
                                                                  \\
+
−
                                        y_2 & = 2\,x + 1
+
−
                          \end{align}</math></td>
+
−
  <td><math> \qquad\qquad </math></td>
+
−
  <td>[[Image: Ex 2.png]]</td>
+
−
</tr>
+
−
</table>
+
−
::Graferna bekräftar att det finns endast en lösning. Även grafernas skärningspunkt <big><math> {2 \over 3} </math></big> bekräftar den lösning vi fått för ekvationen <math> \; \, | \, x - 3 \, | - 2\,x \, = \, 1  \; </math>.
+
−
 
+
−
 
+
−
== <b><span style="color:#931136">Olikheter med absolutbelopp</span></b> ==
+
−
 
+
−
<br>
+
−
 
+
−
<div class="ovnC">
+
−
Lös olikheten <math> \; \, | \, x + 2 \, | \, < \, 4 \, </math>.
+
−
</div>
+
−
 
+
−
 
+
−
:<big><b>Lösning:</b></big>
+
−
 
+
−
::<u><b>Fall 1</b></u> <math> \; x + 2 \geq 0 \quad \; </math> eller <math> \;\quad x \geq -2 </math>
+
−
 
+
−
::Enligt absolutbeloppets definition blir i så fall <math> | \, x + 2 \, | = x + 2\, </math> och olikheten blir:
+
−
 
+
−
::::<math>\begin{align}  x + 2 & < 4    \\
+
−
                        x    & < 4 -2  \\
+
−
                        x    & < 2  \\
+
−
    \end{align}</math>
+
−
 
+
−
::Kombinerad med <u><b>Fall 1</b></u>s förutsättning <math> \; x \geq -2 \; </math> ger detta:
+
−
 
+
−
::<b>Svar för fall 1:</b> <math> \; \;\; -2 \leq x < 2\, </math>
+
−
 
+
−
::<u><b>Fall 2</b></u> <math> \; x + 2 < 0 \quad \; </math> eller <math> \;\quad x < -2 </math>
+
−
 
+
−
::Enligt absolutbeloppets definition blir i så fall <math> | \, x + 2 \, | = -(x + 2) = -x - 2\, </math> och olikheten blir:
+
−
 
+
−
::::<math>\begin{align}  -\,x - 2 & < 4    \\
+
−
                        -\,4 - 2 & < x    \\
+
−
                            -\,6 & < x    \\
+
−
                                x & > -\,6  \\
+
−
          \end{align}</math> 
+
−
 
+
−
::Kombinerad med <u><b>Fall 2</b></u>s förutsättning <math> \; x < -2 \; </math> ger detta:
+
−
 
+
−
::<b>Svar för fall 2:</b> <math> \; \;\; -6 < x < -2\, </math>
+
−
 
+
−
::Om vi nu sammanfogar <b>Svar för fall 1</b> med <b>Svar för fall 2</b> får vi:
+
−
 
+
−
::<b>Olikhetens lösning:</b> <math> \; \;\; -6 < x < 2\, </math>
+
−
 
+
−
::På bilden visas i samma koordinatsystem graferna till de två funktionerna:
+
−
<table>
+
−
<tr>
+
−
  <td><math> \qquad\qquad \begin{align}  y & = | \, x + 2 \, |  \\
+
−
                                                                  \\
+
−
                                        y & = 4
+
−
                          \end{align}</math></td>
+
−
  <td><math> \qquad\qquad </math></td>
+
−
  <td>[[Image: Ex Olikhet.png]]</td>
+
−
</tr>
+
−
</table>
+
−
::Olikhetens lösning är markerad med rött. Den består av alla <math> x \, </math> för vilka grafen till <math> y = | \, x + 2 \, | </math> befinner sig under grafen till <math> y = 4\, </math> dvs alla <math> x \, </math> för vilka <math> | \, x + 2 \, | \, < \, 4 </math>.
+
−
 
+
−
::<b>Svar:</b> Olikheten <math> | \, x + 2 \, | \, < \, 4 </math> har lösningen <math> \, -6 < x < 2 </math> .
+
−
 
+
−
 
+
−
----
+
−
 
+
−
 
+
−
I denna uppgift ovan har vi visat:
+
−
 
+
−
:::::<math> | \, x + 2 \, | \, < \, 4 \quad \Longrightarrow \quad -6 < x < 2 </math>
+
−
 
+
−
I nästa uppgift visas att även det omvända gäller:
+
−
 
+
−
:::::<math> | \, x + 2 \, | \, < \, 4 \quad \Longleftarrow \quad -6 < x < 2 </math>
+
−
 
+
−
Dvs vi har ekvivalens mellan olikheten och intervallet:
+
−
 
+
−
:::::<math> | \, x + 2 \, | \, < \, 4 \quad \Longleftrightarrow \quad -6 < x < 2 </math>
+
−
 
+
−
 
+
−
== <b><span style="color:#931136">Intervall med absolutbelopp</span></b> ==
+
−
 
+
−
 
+
−
<div class="ovnA">
+
−
Skriv om intervallet <math> \; -6 < x < 2 \; </math> till en olikhet med hjälp av absolutbelopp.
+
−
</div>
+
−
 
+
−
:Vi vänder alltså på frågeställningen:
+
−
 
+
−
:Vi antar att vi har lösningen <math> \; -6 < x < 2 \; </math> och söker olikheten som har denna lösning.
+
−
 
+
−
 
+
−
<big><b>Lösning:</b></big>
+
−
 
+
−
:Sådana uppgifter löses i två steg:
+
−
 
+
−
<div style="border:1px solid black;display:inline-block !important;margin-left: 50px !important;padding:10px 20px 10px 20px; -webkit-border-radius: 5px; -moz-border-radius: 5px;border-radius: 5px;">
+
−
* Hitta intervallets mittpunkt som vi kallar <math> {\rm M } </math>.
+
−
 
+
−
* Hitta intervallets halva längd eller intervallets "radie" som vi kallar <math> {\rm r } </math>.
+
−
</div>
+
−
 
+
−
:Då kan intervallet skrivas om till olikeheten: &nbsp;&nbsp;&nbsp;&nbsp; <math> | \, x \,- {\rm M } \, | < \, {\rm r } </math> &nbsp; .
+
−
 
+
−
:Låt oss börja med att hitta mittpunkten till intervallet <math> \,-6 < x < 2 </math>. Det görs bäst med intervallgränsernas <strong><span style="color:red">medelvärde</span></strong><span style="color:black">:</span>
+
−
 
+
−
::<math> {\rm M } = {-6 + 2 \over 2} = {-4 \over 2} = -2 </math>
+
−
 
+
−
:Sedan beräknar vi intervallets halva längd genom dra av intervallgränserna från varandra (oavsett ordning), dela med 2 och sätta det hela inom absolutbelopp eftersom längd alltid är positiv<span style="color:black">:</span>
+
−
 
+
−
::<math> {\rm r } = \left| {-6 - 2 \over 2} \, \right| = \left| {-8 \over 2} \, \right| = | -4 \, | = 4 </math>
+
−
 
+
−
:Därmed kan intervallet skrivas om till olikeheten<span style="color:black">:</span>
+
−
 
+
−
::<math> \; | \, x \,- {\rm M } \, | < \, {\rm r } \; = \; | \, x - (-2) \, | < 4 \; \; {\rm dvs} \; \; | \, x + 2 \, | < 4 </math>
+
−
 
+
−
:<b>Svar:</b> Intervallet <math> -6 < x < 2 \, </math> kan skrivas om till olikheten <math> | \, x + 2 \, | \, < \, 4 </math> .
+
−
 
+
−
 
+
−
----
+
−
 
+
−
 
+
−
Med de beteckningar som vi införde ovan kan vi sammanfattningsvis formulera ekvivalensen mellan olikhet och intervall:
+
−
 
+
−
 
+
−
<div style="border:1px solid black;display:inline-block !important;margin-left: 50px !important;padding:10px 20px 10px 20px; -webkit-border-radius: 5px; -moz-border-radius: 5px;border-radius: 5px;"><big><strong><math> | \, x - {\rm M } \, | \, < \, {\rm r } \qquad \Longleftrightarrow \qquad {\rm M } - {\rm r } \; < \; x \; < \; {\rm M } + {\rm r } </math></strong></big>
+
−
</div>
+
−
 
+
−
 
+
−
där <math> {\rm M } </math> är intervallets mittpunkt och <math> {\rm r } </math> intervallets halva längd eller "radie".
+
−
 
+
−
För att beskriva en (sammanhängande) talmängd kan man antingen använda en olikhet med absolutbelopp eller ett intervall.
+
−
 
+
−
Valet av beteckningarna <math> {\rm M } </math> för mittpunkten och <math> {\rm r } </math> för "radien" ska associera tankarna till den tvådimensionella generaliseringen av olikheten &nbsp; <math> | x - {\rm M } | < {\rm r } </math> &nbsp; till &nbsp; <math> || x - {\rm M } || < {\rm r } </math> . Här har absolutbeloppet <math> \; {\color{Red} |} \, \quad \, {\color{Red} |} \; </math> ersatts av något som kallas norm <math> \; {\color{Red} {||}} \, \quad \, {\color{Red} {||}} \; </math> och fortfarande kan tolkas som <strong><span style="color:red">avstånd</span></strong>, fast nu mellan två punkter. Den nya olikheten beskriver en punktmängd bestående av alla punkter <math> \,x  </math> i planet som ligger i en cirkel med medelpunkten <math> {\rm M } </math> och radien <math> {\rm r } </math>. Cirkeln är då generaliseringen av intervallet. Ersätter man olikhetstecknet med likhet får man cirkelns ekvation &nbsp; <math>|| x - {\rm M } || = {\rm r }</math>, mängden av alla punkter <math> \,x  </math> som har samma avstånd <math> {\rm r } </math> från medelpunkten <math> {\rm M } </math>.
+
  
 +
Graferna visar att det finns två lösningar: två skärningspunkter.
  
 +
Skärningspunkternas <math> \, x</math>-koordinater <math> \, x_1 = 2\, </math> och <math> \, x_2 = -4\, </math> bekräftar de lösningar vi fått för ekvationen.
  
  
Rad 531: Rad 384:
  
  
−
[[Matte:Copyrights|Copyright]] © 2011-2015 Taifun Alishenas. All Rights Reserved.
+
 
 +
 
 +
 
 +
[[Matte:Copyrights|Copyright]] © 2019 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved.

Nuvarande version från 11 februari 2025 kl. 13.48

        <<  Förra avsnitt          Genomgång          Övningar          Diagnosprov 1 kap 1          Diagnosprov 2 kap 1      
                 Fördjupning                    Lösningar Diagnos 1          Lösningar Diagnos 2      


Några exempel på absolutbelopp


Exempel 1    Åldersskillnad

En dejtingsajt på nätet har bestämt sig för att åldersskillnaden mellan två partner ska vara \( \, < \, 6 \, \) år.

I sina webbformulär använder de följande formel som ger utskrifterna till höger

efter att några kunder skickat in sina uppgifter:

\( \mbox{Age}_\mbox{male} - \mbox{Age }_\mbox{female}\, \)
 \( \qquad\qquad \) \( 25 \quad - \quad 20 \quad = \quad 5 \)

\( 26 \quad - \quad 22 \quad = \quad 4 \)

\( 23 \quad - \quad 30 \quad = \quad {\color{Red} {\boxed{-7}}} \)		 \( \quad \) \( < \; 6 \quad \Rightarrow \quad {\rm ok} \)

\( < \; 6 \quad \Rightarrow \quad {\rm ok} \)

\( < \; 6 \quad \Rightarrow \quad {\rm {\color{Red} {\bf{ok}}}} \)

Lovisa som sommarjobbar på dejtingsajten konstaterar att den sista utskriften ger fel resultat: Åldersskillnaden är \( \, > \, 6 \, \) år.

Felet beror på att negativ åldersskillnad inte är meningsfull. Åldersskillnad måste alltid vara positiv.

Lovisa som lärt sig absolutbelopp på Matte 3-kursen föreslår att man ändrar formeln. Efter ändringen blir det så här:

\( { \color{Red} |} \, \mbox{Age}_\mbox{male} - \mbox{Age }_\mbox{female} \, { \color{Red} |} \)
 \( \qquad\quad \) \( { \color{Red} |} \, 25 \quad - \quad 20 \, { \color{Red} |} \quad = \quad 5 \)

\( { \color{Red} |} \, 26 \quad - \quad 22 \, { \color{Red} |} \quad = \quad 4 \)

\( { \color{Red} |} \, 23 \quad - \quad 30 \, { \color{Red} |} \quad = \quad {\color{Red} {\boxed{7}}} \)		 \( \quad \) \( < \; 6 \quad \Rightarrow \quad {\rm ok} \)

\( < \; 6 \quad \Rightarrow \quad {\rm ok} \)

\( {\color{Red} {\bf{>}}} \,\; 6 \quad \Rightarrow \quad {\rm {\color{Red} {\bf{inte\;ok}}}} \)

Nu stämmer det, vilket beror på att Lovisa infogade de två raka strecken \( \; {\color{Red} |} \, \quad \, {\color{Red} |} \; \) i formeln, vilket korrigerade den sista utskriften:

\[ { \color{Red} |} \, 23 \quad - \quad 30 \, { \color{Red} |} \quad = \quad { \color{Red} |} \, - 7 \, { \color{Red} |} \quad = \quad 7 \]

\( \; {\color{Red} |} \, \quad \, {\color{Red} |} \; \) tar bort minustecknet från \( -7\, \) och ger \( 7\, \). Därför: \( { \color{Red} |} \, - 7 \, { \color{Red} |} = 7 \).


De två raka strecken \( \; {\color{Red} |} \, \quad \, {\color{Red} |} \; \) som skrivs kring ett tal eller ett uttryck, kallas för absolutbelopp och betyder:

Att göra om ett negativt tal till ett positivt tal och låta ett positivt tal vara oförändrat.    

Kortare:    Ett tals absolutbelopp är talets positiva värde, t.ex.:

\[ | \, - 7 \, | \, = \, 7 \]
\[ | \, - 0,5 \, | \, = \, 0,5 \]
\[ \left| \, - \sqrt{5} \, \right| \, = \, \sqrt{5} \]
\( \qquad\quad \)
\[ | \; 23 \; | \, = \, 23 \]
\[ | \, 7,25 \, | \, = \, 7,25 \]
\[ \left| \, 0 \, \right| \, = \, 0 \]
\( \qquad\quad \)
\[ \displaystyle{ \left| \, {13\over 4} \, \right| \, = \, {13\over 4} } \]
\[ \displaystyle{ \left| \, - {2\over 3} \, \right| \, = \, {2\over 3} } \]
\[ \left| \, \sqrt{3} \, \right| \, = \, \sqrt{3} \]
\( \qquad\quad \)
\[ | \, a \, - \, b \, | \, = \, | \, b \, - \, a \, | \] (se Exempel 2)
\[ | \, i \, | \, = \, | \, \sqrt{-1} \, | \, = \, 1 \] (se Exempel 3)

Absolutbelopp lämpar sig för att modellera storheter som till sin natur är positiva som t.ex. åldersskillnad.

Andra exempel är avstånd, längd, area, volym, massa (vikt), tid, lufttryck, vindstyrka, pengar, antal objekt, \( \, \ldots \; \).

Vi tittar närmare på avstånd:

Exempel 2    Avstånd mellan två tal

Vad är avståndet mellan \( \, 2 \, \) och \( \, 5 \, \)?    Svar: \( \quad 5 \, - \, 2 \, = \, 3 \)

Vad är då avståndet mellan \( -2 \, \) och \( -5 \, \)? Gör man samma sak blir svaret: \( \quad -5 \, - \, (-2) \, = \, -5 \, + \, 2 \, = \, -3 \)

Men vi vet att avståndet mellan \( -2 \, \) och \( -5 \, \) är \( 3 \, \) och inte \( -3 \, \). Ett avstånd kan inte vara negativt. Avstånd är alltid positivt.

Korrekt svar:

\[ {\color{Red} |} \, -5 - (-2) \, { \color{Red} |} \; = \; { \color{Red} |} -5 + 2 \, { \color{Red} |} \, = \, { \color{Red} |} -3 \, { \color{Red} |} \; = \; 3 \]

Fortfarande dras talen av från varandra, men absolutbelopp kring subtraktionen gör att resultatet blir positivt.

Kastar vi om talens ordning blir det samma resultat:

\[ { \color{Red} |} \, -2 - (-5) \, { \color{Red} |} \; = \; { \color{Red} |} -2 + 5 \, { \color{Red} |} \, = \, { \color{Red} |} \, 3 \, { \color{Red} |} \; = \; 3 \]

Generellt gäller:

Absolutbeloppet \( \; | \, a - b \, | \; \) är avståndet mellan talen \( \, a \, \) och \( \, b \, \).

Det är irrelevant i vilken ordning talen skrivs. Det gäller: \( \quad | \, a - b \, | \, = \, | \, -(b - a) \, | \, = \, | \, b - a \, | \)


Ett specialfall av avståndet mellan två tal är, när det ena talet är \( \, 0 \, \):

Exempel 3    Avstånd från \( \, 0 \, \)

Om vi i den nya definitionen för avstånd \( \, | \, a - b \, | \, \) sätter in \( a = 0 \, \) och \( b = -5 \, \) för att beräkna avståndet mellan \( 0 \, \) och \( -5 \, \) får vi:

\[ | \, 0 - (-5) \, | \, = \, | \, 0 + 5 \, | \, = \, | \, 5 \, | \, = \, 5 \]

Och tar vi \( \, | \, b - a \, | \, \) blir det samma resultat:

\[ | -5 - 0 \, | \, = \, | -5 \, | \, = \, 5 \]

\( 5 \, \) är alltså talet \( \, -5\):s avstånd från \( 0 \, \).

Detta ger oss en ny tolkning av absolutbeloppet som gäller för alla tal, även för komplexa (se exemplet \( | \, i \, | = 1 \) ovan och motivera!):

Absolutbeloppet \( \; | \, a \, | \; \) är talet \( a\):s avstånd från 0.


Alla hittills nämnda tolkningar av absolutbeloppet är utmärkta att använda i många sammanhang och ger oss en bra intuitiv uppfattning av begreppet.

Men de är inga strikt matematiska definitioner och lämpar sig inte t.ex. för att lösa ekvationer eller olikheter som involverar absolutbelopp. Därför:


Allmän definition, funktion och graf

Absolutbeloppet \( \; | \, x \, | \; \) av ett tal \( x\, \) definieras genom:
\[ | \, x \, | \, = \, \begin{cases} \;\, x & \mbox{om } x \geq 0 \\ -x & \mbox{om } x < 0 \\ \end{cases} \]

Grafen till   funktionen \( \; y = | \, x \, | \; \) ser ut så här:

\( \qquad \) Övn 8.png

Absolutbeloppet är en funktion som är definierad och kontinuerlig för alla \( x \, \).


OBS!   I följande exempel ska absolutbelopp bestämmas genom att använda den allmänna definitionen, inte intuitivt.

Exempel 1:

Vad är \( | \, 7 \, | \) enligt definitionen ovan?
Eftersom \( x = 7 \geq 0 \) väljs det första alternativet (första raden) i definitionen efter klammern \( \begin{cases} \end{cases} \), dvs \( | \, 7 \, | = 7\, \).
Svar: \( \; | \, 7 \, | = 7 \).


Exempel 2:

Vad är \( | \, - 5 \, | \) enligt definitionen ovan?
Eftersom \( x = -5 < 0\, \) väljs det andra alternativet (andra raden) i definitionen efter klammern \( \begin{cases} \end{cases} \), dvs \( | \, - 5 \, | \, = \, -(-5) \, = \, 5 \).
Svar: \( \; | \, - 5 \, | = 5 \).


Exempel 3:

Vad är \( | \, 0 \, | \) enligt definitionen ovan?
Eftersom \( x = 0 \geq 0 \) väljs det första alternativet (första raden) i definitionen efter klammern \( \begin{cases} \end{cases} \), dvs \( | \, 0 \, | = 0\, \).
Svar: \( \; | \, 0 \, | = 0 \).


Exempel 4:

Vad är \( | \, a + 2 \, | \) enligt definitionen ovan?
Eftersom vi inte känner till \( \, a\):s värde och därför inte vet om \( \, a + 2 \) blir positivt eller negativt, måste vi skilja mellan två fall:
Fall 1 \( \quad a + 2 \geq 0 \quad \; \) eller \( \;\quad a \geq -2 \)
Eftersom \( x = a + 2 \geq 0 \) väljs det första alternativet (första raden) i definitionen efter klammern \( \begin{cases} \end{cases} \), dvs \( | \, a + 2 \, | = a + 2\, \).
Fall 2 \( \quad a + 2 < 0 \quad \; \) eller \( \;\quad a < -2 \)
Eftersom \( \; x = a + 2 < 0\, \) väljs det andra alternativet (andra raden) i definitionen efter klammern \( \begin{cases} \end{cases} \), dvs \( | \, a + 2 \, | \, = \, -(a + 2) \, = \, -a - 2\, \).
Svar: \( \; | \, a + 2 \, | \, = \, \begin{cases} \;\, a + 2 & \mbox{om } a \geq -2 \\ -a-2 & \mbox{om } a < -2 \\ \end{cases} \)


Exempel 4 visar: Vill man bli av med absolutbeloppstecknen i ett uttryck som involverar obekanta variabler, måste man alltid skilja mellan två olika fall enligt absolubeloppets allmänna definition. Detta kommer vi att göra nu hela tiden när vi löser ekvationer och olikheter som involverar absolutbelopp.


Ekvationer med absolutbelopp


Lös ekvationen \( \; \, | \, x + 1 \, | \, = \, 3 \)


Eftersom vi inte känner till \( \, x \, \) måste vi skilja mellan två fall, när vi tillämpar absolutbeloppets definition:

Fall 1 \( \quad x + 1 \geq 0 \quad \; \) eller \( \;\quad x \geq -1 \)

Enligt absolutbeloppets definition väljs det första alternativet efter klammern \( \begin{cases} \end{cases} \), dvs \( | \, x + 1 \, | \) blir \( x + 1\, \).

Dvs i det här fallet kan vi ta bort absolutbeloppstecknen utan åtgärd. Ekvationen blir:

\[\begin{align} x + 1 & = 3 \\ x & = 3 - 1 \\ x_1 & = 2 \end{align}\]

Vi kollar om lösningen inte står i motsats till förutsättningen vi gjorde i Fall 1, nämligen \( \, x \geq -1 \).

Men faktiskt är \( 2 \geq -1 \). Därmed kan vi godta denna lösning.

Annars hade den varit en s.k. falsk rot, dvs en beräknad "rot" som inte uppfyller ekvationen, se Falska rötter.

I ekvationer med absolutbelopp är sådana kontroller kring falska rötter obligatoriska.

Fall 2 \( \quad x + 1 < 0 \quad \; \) eller \( \;\quad x < -1 \)

Enligt absolutbeloppets definition väljs det andra alternativet efter klammern \( \begin{cases} \end{cases} \), dvs \( | \, x + 1 \, | \) blir \( -(x + 1) = -x - 1\, \).

Dvs i det här fallet måste vi ersätta \( x + 1\, \) med \( -x - 1\, \), när vi tar bort absolutbeloppstecknen. Ekvationen blir:

\[\begin{align} -x - 1 & = 3 \\ -3 - 1 & = x \\ -4 & = x \\ x_2 & = -4 \end{align}\]

Även här måste vi kolla om lösningen är förenlig med förutsättningen vi gjorde i Fall 2, nämligen \( \, x < -1\, \).

Men faktiskt är \( -4 < -1\, \). Därmed kan vi godta även denna lösning. Ekvationen har två lösningar.

Svar:
\( x_1 = 2 \quad {\rm och} \quad x_2 = -4 \)

Ekvationens och lösningarnas grafiska tolkning:

Vi ritar i samma koordinatsystem graferna till de två funktioner som står i ekvationens resp. led:

\( \qquad\qquad \begin{align} y_1 & = | \, x + 1 \, | \\ \\ y_2 & = 3 \end{align}\) \( \qquad\qquad \) 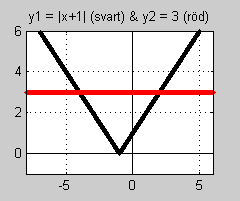Ex 1a.png

Likheten mellan leden: \( \, | \, x + 1 \, | \, = \, 3 \, \) innebär att ekvationens lösningar är skärningspunkternas \( \, x\)-koordinater.

Graferna visar att det finns två lösningar: två skärningspunkter.

Skärningspunkternas \( \, x\)-koordinater \( \, x_1 = 2\, \) och \( \, x_2 = -4\, \) bekräftar de lösningar vi fått för ekvationen.


Internetlänkar

http://www.youtube.com/watch?v=cmAoY6RaKGU

http://www.youtube.com/watch?v=Ox55mE8N0qY

http://people.su.se/~matamm/undervisning/pdf/Introduktionskurs/Dag%203.pdf

http://ingforum.haninge.kth.se/armin/ALLA_KURSER/SF1625/ABSOLUTBELOPP.pdf






Copyright © 2019 TechPages AB. All Rights Reserved.

Hämtad från "https://matte3c.mathonline.se/index.php?title=1.6_Absolutbelopp&oldid=36977"