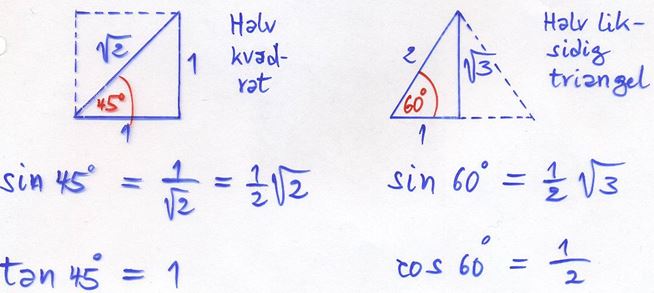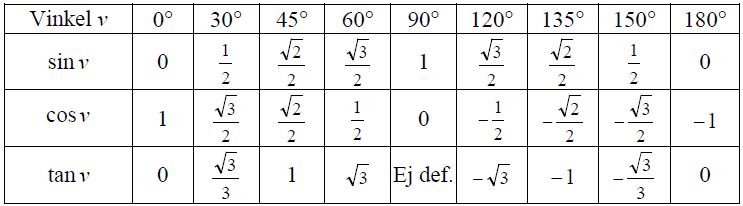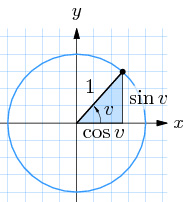Skillnad mellan versioner av "Kapitel 5 Trigonometri"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (530 mellanliggande versioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
__NOTOC__ | __NOTOC__ | ||
| + | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| + | | style="border-bottom:1px solid #797979" width="5px" | | ||
| + | {{Not selected tab|[[Kapitel 4 Integraler| << Förra kapitel]]}} | ||
| + | {{Selected tab|[[Kapitel 5 Trigonometri|Kap 5 Trigonometri]]}} | ||
| + | {{Not selected tab|[[Media: Formelsamling NP Ma3 Trig.pdf|Formelsamling Trigonometri]]}} | ||
| + | {{Not selected tab|[[Matte 3c Planering|Planering Matte 3c]]}} | ||
| + | {{Not selected tab|[[Diagnosprov kap 4 och 5 Integraler och Trigonometri|Diagnos kap 4-5 Integr. & Trigon.]]}} | ||
| + | | style="border-bottom:1px solid #797979" width="100%"| | ||
| + | |} | ||
| + | |||
<big> | <big> | ||
| + | <br> | ||
| + | Detta kapitels övningar finns inte på webben (pga tidsbrist). Därför: | ||
| + | |||
| + | Läs igenom genomgångarna här, men använd för övningarna boken <i>Matematik 5000</i>. | ||
| + | |||
== <b><span style="color:#931136">Utdrag ur planeringen:</span></b> == | == <b><span style="color:#931136">Utdrag ur planeringen:</span></b> == | ||
<br> | <br> | ||
| − | <div style="border:1px solid black;display:inline-table;margin-left: 30px;"> [[Image: | + | <div style="border:1px solid black;display:inline-table;margin-left: 30px;"> [[Image: Planering_Integr_Rubrik_2019_800a.jpg]] </div> |
| − | + | <div style="border:1px solid black;display:inline-table;margin-left: 30px;"> [[Image: Planering_Trigonometri_2019_800b.jpg]] </div> | |
| + | <br> | ||
| + | == <b><span style="color:#931136">5.1 Trigonometri i rätvinkliga trianglar <math> \qquad\;\; </math> <small><small>Övningar: Boken, sid 208</small></small></span></b> == | ||
| + | <br> | ||
| + | <big><b><span style="color:#931136">Tangens för <math> \, v \, < \, 90^\circ </math></span></b></big> | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 1 Tangens_55.jpg]] </div> | ||
| − | == <b><span style="color:#931136">5. | + | <div class="ovnA"> |
| + | <big>{{#NAVCONTENT:Flera exempel på tangens|Exempel på tangens}}</big> | ||
| + | </div> | ||
| + | </td> | ||
| + | <td><div style="border:1px solid black;display:inline-table;margin-left: 20px;"> [[Image: 2 Tangensproblemet_55.jpg]] </div> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 12px;"> [[Image: 3 OmvantProblem_55.jpg]] </div> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | |||
| + | <big><b><span style="color:#931136">Sinus och Cosinus för <math> \, v \, < \, 90^\circ </math></span></b></big> | ||
| + | |||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 5 SinusCosinus_55.jpg]] </div> | ||
| + | <br> | ||
| + | == <b><span style="color:#931136">5.2 Exakta trigonometriska värden / Enhetscirkeln <math> \;\; </math> <small><small>Övningar: Boken, sid 209 / 210</small></small></span></b> == | ||
<br> | <br> | ||
| − | <big><b><span style="color:#931136"> | + | <big><b><span style="color:#931136">Två speciella vinklar<span style="color:black">:</span> <math> \, 45^\circ \, </math> och <math> \, 60^\circ \, </math> </span></b></big> |
| − | < | + | Pythagoras satsen används på halva kvadraten med sidan <math> \, 1 \, </math> för att få diagonalen <math> \, \sqrt{2} </math>. Sedan bestäms <math> \, \sin 45^\circ \, </math> och <math> \, \tan 45^\circ </math><span style="color:black">:</span> |
| + | <div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 6_Exakta_trig_varden_45_60.jpg]] </div> | ||
| − | < | + | På liknande sätt används Pythagoras på halva liksidiga triangeln med sidan <math> \, 2 \, </math> för att få höjden <math> \, \sqrt{3} </math>. Sedan bestäms <math> \, \sin 60^\circ </math> och <math> \, \cos 60^\circ </math>. |
| + | "Exakt" betyder: Gå inte över till decimaltal, dvs: | ||
| − | + | ::* Bibehåll bråk med endast heltal i täljare och nämnare, | |
| + | ::* Bibehåll rötter som inte ger heltal. | ||
| + | En konsekvens blir att inte ens rötter ska stå kvar i bråkens nämnare. Ta upp dem genom förlängning med <math> \, \sqrt{{\color{White} {\cdots}}} </math>, t.ex.<span style="color:black">:</span> | ||
| − | + | ::<math> \displaystyle \frac{1}{\sqrt{2}} \, = \, \frac{1 \, \cdot \, {\color{Red} {\sqrt{2}}}}{\sqrt{2} \cdot {\color{Red} {\sqrt{2}}}} \, = \, \frac{\sqrt{2}}{2} \, = \, \frac{1}{2} \, \sqrt{2} </math> | |
| − | < | + | |
| + | <big><b><span style="color:#931136">Ytterligare exakta trigonometriska värden </span></b></big> | ||
| + | |||
| + | Andra geometriska satser ger följande exakta värden<span style="color:black">:</span> | ||
| + | |||
| + | <div style="border:0px solid black;display:inline-table;margin-left: 10px;"> [[Image: 6_Exakta_trig_varden.jpg]] </div> | ||
| + | |||
| + | |||
| + | <big><b><span style="color:#931136">Enhetscirkeln</span></b></big> | ||
| + | |||
| + | ''Cirkel'' <math> \, = \, </math> Mängden av alla punkter som har samma avstånd (radien <math> \, r \, </math>) från en punkt (medelpunkten <math> \, M \, </math>). | ||
| + | |||
| + | Cirkelns ekvation: | ||
| + | |||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 7_Cirkelns_ekvation_70.jpg]] </div> | ||
| + | |||
| + | |||
| + | ''Enhetscirkeln'' är cirkeln med radien <math> \, r \, = \, 1 \, </math> och medelpunkten <math> \, M \, = \, O \, </math> (origo). | ||
| + | |||
| + | Om en punkt <math> \, P\,(x, y) \, </math> snurrar på enhetscirkeln och <math> \, v \, </math> är vinkeln mellan <math> \, x</math>-axeln och <math> \, \overline{OP} </math>, så gäller<span style="color:black">:</span> | ||
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td><math> \quad </math></td> | + | <td><div style="border:0px solid black;display:inline-table;margin-left: 25px;"> [[Image: 7_Enhetscirkeln.jpg]] </div> |
| − | <td> | + | </td> |
| + | <td><math> \qquad\qquad\quad </math> | ||
| + | </td> | ||
| + | <td><div class="border-divblue"> | ||
| + | <math>\begin{array}{rcl} x & = & \cos v \\ | ||
| + | y & = & \sin v | ||
| + | \end{array}</math></div> | ||
| + | |||
| − | |||
| − | |||
| − | |||
</td> | </td> | ||
| − | |||
| − | |||
</tr> | </tr> | ||
</table> | </table> | ||
| + | I cirklar med radien <math> \, r \, > \, 1 \, </math> förblir vinkeln <math> \, v \, </math> den samma och därmed <math> \, \cos v = \displaystyle \frac{r \cdot \; x}{r} = x \, </math> och <math> \, \sin v = \displaystyle \frac{r \cdot \; y}{r} = y </math>, precis som ovan. | ||
| + | Detta används för att definiera de trigonometriska funktionerna i godtyckliga trianglar, dvs för vinklar <math> \, v \, \geq \, 90^\circ \, </math>. | ||
| − | |||
| − | |||
| − | :: | + | == <b><span style="color:#931136">5.3 Godtyckliga trianglar <math> \qquad\qquad\;\; </math> <small><small>Övningar: Boken, sid 215 </small></small></span></b> == |
| − | + | <br> | |
| − | + | <big><b><span style="color:#931136">Sinus och Cosinus för vinklar i intervallet<span style="color:#931136">:</span> <math> \quad 90^\circ \, \leq \, v \, \leq \, 180^\circ </math> </span></b></big> | |
| − | + | ||
| − | + | Exempel<span style="color:black">:</span> | |
| − | + | :::<math> \sin 150^\circ \, = \, \sin (180^\circ - 30^\circ) \, = \, \sin 30^\circ \, = \, \frac{1}{2} </math> | |
| − | + | :::<math> \cos 120^\circ \, = \, \cos (180^\circ - 60^\circ) \, = \, -\cos 60^\circ \, = \, -\frac{1}{2} </math> | |
| − | + | Förklaring med enhetscirkeln: | |
| − | |} | + | |
| + | Punkten till vinkeln <math> \, v \, </math> har samma <math> \, y</math>-koordinat (<math>=\sin v</math>) som punkten till vinkeln <math> \, 180-v </math>. | ||
| + | |||
| + | Punkten till vinkeln <math> \, v \, </math> har samma <math> \, x</math>-koordinat (<math>=\cos v</math>) som punkten till vinkeln <math> \, 180-v \, </math> med omvänt tecken. | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 8 Godtyckliga trianglar_400.jpg]] </div> | ||
| + | </td> | ||
| + | <td><big><b> <span style="color:#931136">Ekvationer</span> | ||
| + | |||
| + | <span style="color:#931136">med</span> | ||
| + | |||
| + | <span style="color:#931136">Sin & Cos:</span></b></big> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | </td> | ||
| + | <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 9 Ex Godtyckliga vinklar_400.jpg]] </div> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | |||
| + | <big><b><span style="color:#931136">Sinus, Cosinus och Tangens för alla vinklar</span></b></big> | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 10 Alla vinklar_400.jpg]] </div> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | </td> | ||
| + | <td><big><b> <span style="color:#931136">En gång till</span> | ||
| + | |||
| + | <span style="color:#931136">Sin & Cos</span> | ||
| + | |||
| + | <span style="color:#931136">för <math> v \geq 90^\circ </math></span> | ||
| + | |||
| + | <span style="color:#931136">i trianglar:</span></b></big> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | </td> | ||
| + | <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 10a En gang till Sin Cos 400.jpg]] </div> | ||
| + | |||
| + | |||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | <div class="border-divblue">En <b><span style="color:red">sinus</span></b>ekvation har i intervallet <math> \, 0^\circ \leq v \leq 180^\circ \, </math> alltid <b><span style="color:red">två</span></b> lösningar.<br><br> | ||
| + | En <b><span style="color:red">cosinus</span></b>ekvation har i intervallet <math> \, 0^\circ \leq v \leq 180^\circ \, </math> <b><span style="color:red">endast en</span></b> lösning.</div> | ||
| + | |||
| + | |||
| + | == <b><span style="color:#931136">5.4 Triangelsatserna <math> \qquad\qquad\qquad\;\; </math> <small><small>Övningar: Boken, sid 218 </small></small></span></b> == | ||
| + | |||
| + | |||
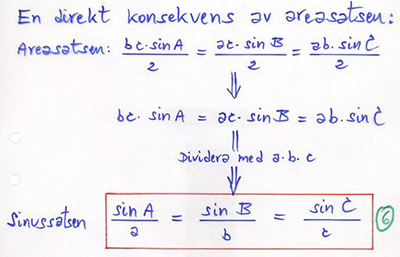
| + | Det finns tre triangelsatser: <b><span style="color:#931136">Areasatsen</span></b>, <b><span style="color:#931136">Sinussatsen</span></b> och <b><span style="color:#931136">Cosinussatsen</span></b>. | ||
| + | |||
| + | Triangelsatsernas formulering baseras på de standardbeteckningar för trianglar som införs här: | ||
| + | |||
| + | <big><b><span style="color:#931136">Areasatsen</span></b></big> | ||
| + | |||
| + | <u>Givet:</u> <math> \quad </math> Två sidor och den mellanliggande vinkeln i en triangel. | ||
| + | |||
| + | <u>Sökt:</u> <math> \quad\, </math> Triangelns area. | ||
| + | |||
| + | <table> | ||
| + | <tr> | ||
| + | <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 11 Areasatsen_400_0b.jpg]]</div> | ||
| + | |||
| + | |||
| + | |||
| + | </td> | ||
| + | <td> </td> | ||
| + | <td> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 11 Areasatsen_400a.jpg]]</div> | ||
| + | |||
| + | Areasatsen i vanliga ord (utan beteckningar): | ||
| + | |||
| + | <div class="border-divblue">En triangels area är produkten av <b><span style="color:red">två sidor</span></b> | ||
| + | |||
| + | och den <b><span style="color:red">mellanliggande vinkelns</span></b> sinus, | ||
| + | |||
| + | delad med <math> \, 2 \, </math> (<b><span style="color:red">SVS</span></b>-struktur).</div> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
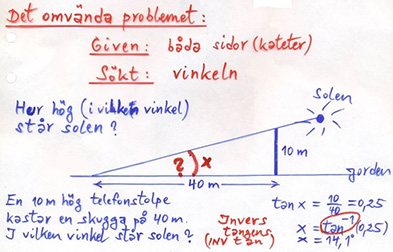
| + | <big><b><span style="color:#931136">Det omvända problemet:</span></b></big> | ||
| + | |||
| + | <u>Givet:</u> <math> \quad </math> Arean och två sidor av en triangel. | ||
| + | |||
| + | <u>Sökt:</u> <math> \quad\, </math> Den mellanliggande vinkeln <math> \, v \, </math>. | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 11 Areasatsen_400_0c.jpg]]</div> | ||
| + | |||
| + | </td> | ||
| + | <td> </td> | ||
| + | <td> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <div class="ovnE"> | ||
| + | {{#NAVCONTENT:Varför två lösningar?|Varför två lösningar}} | ||
</div> | </div> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | Det geometriska problemet har två lösningar. Areasatsen ger båda: | ||
| + | Areasatsen leder till en sinusekvation som pga sina två lösningar resulterar i två vinklar och därmed två trianglar. | ||
| − | |||
| − | :: | + | == <b><span style="color:#931136">5.5 Sinussatsen <math> \qquad\qquad\qquad\;\; </math> <small><small>Övningar: Boken, sid 220 / 224-225 </small></small></span></b> == |
| − | < | + | <u>Givet:</u> <math> \quad </math> Två sidor och en vinkel eller två vinklar och en sida i en triangel. |
| + | |||
| + | <u>Sökt:</u> <math> \quad\, </math> Triangelns tredje sida eller två andra sidor. | ||
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td><div | + | <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 12 Sinussatsen_400.jpg]] </div> |
| − | + | ||
| − | -- | + | |
| − | + | ||
| − | + | </td> | |
| − | + | <td> </td> | |
| − | <td | + | <td> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | </div></td> | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Sinussatsen i vanliga ord (utan beteckningar): | ||
| + | |||
| + | <div class="border-divblue">I en triangel är kvoten mellan | ||
| + | |||
| + | vinklarnas sinus och deras | ||
| + | |||
| + | motstående sidor lika stor.</div> | ||
| + | |||
| + | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
| − | + | ==== <b><span style="color:#931136">Exempel på sinussatsen (två lösningar)</span></b> ==== | |
| + | <u>Givet:</u> <math> \quad </math> Två sidor och den vinkel som inte ligger mellan dem (icke-SVS-struktur). | ||
| − | + | <u>Sökt:</u> <math> \quad\, </math> Triangelns tredje sida. | |
| − | + | ||
| − | + | ||
| − | <div style="border:1px solid black;display:inline-table;margin-left: | + | <table> |
| + | <tr> | ||
| + | <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 12 Sinussatsens_2_fall_400.jpg]] </div> | ||
| + | </td> | ||
| + | <td> </td> | ||
| + | <td> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == <b><span style="color:#931136"> | + | |
| + | <div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 12 Tva trianglar.jpg]] </div> | ||
| + | </td> | ||
| + | <td> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <div class="ovnE"> | ||
| + | {{#NAVCONTENT:Varför två lösningar?|Varför två lösningar}} | ||
| + | </div> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | Att det finns två lösningar (två trianglar) beror på att problemet inte har [[Kapitel_5_Trigonometri#5.4_Triangelsatserna_.5C.28_.5Cqquad.5Cqquad.5Cqquad.5C.3B.5C.3B_.5C.29_.C3.96vningar:_.C2.A0_Boken.2C_sid_218|<b><span style="color:blue">SVS</span></b>]]-struktur, dvs: | ||
| + | |||
| + | Triangelns två sidor <math> \, b = 27 \, </math> och <math> \, c = 35 \, </math> är givna, men inte den mellanliggande vinkeln, utan den som ligger mittemot <math> \, b </math>. | ||
| + | |||
| + | |||
| + | == <b><span style="color:#931136">5.6 Cosinussatsen <math> \qquad\qquad\qquad\;\; </math> <small><small>Övningar: Boken, sid 229-230 </small></small></span></b> == | ||
| + | |||
| + | <u>Givet:</u> <math> \quad </math> Två sidor och en vinkel i en triangel. | ||
| + | |||
| + | <u>Sökt:</u> <math> \quad\, </math> Triangelns tredje sida. | ||
| + | |||
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td>< | + | <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 13 Cosinussatsen_400.jpg]] </div> |
| − | + | ||
| + | </td> | ||
| + | <td> </td> | ||
| + | <td> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <div class="border-divblue">Cosinussatsen utvidgar Pythagoras med | |
| + | |||
| + | en <math> \cos</math>-term som involverar högerledets | ||
| + | |||
| + | två sidor och den mellanliggande vinkeln.</div> | ||
| + | |||
</td> | </td> | ||
| − | |||
| − | |||
</tr> | </tr> | ||
</table> | </table> | ||
| − | <div style="border:1px solid black;display:inline-table;margin-left: | + | |
| + | Pythagoras är ett specialfall av cosinussatsen för fallet<span style="color:black">:</span> <math> \; A , B , {\rm eller\;} C \, = \, 90^\circ \; \Rightarrow \; \cos 90^\circ \, = \, 0 </math>. Då försvinner <math> \cos</math>-termen i cosinussatsen. | ||
| + | |||
| + | När två sidor och den mellanliggande vinkeln i en triangel är givna ([[Kapitel_5_Trigonometri#5.4_Triangelsatserna_.5C.28_.5Cqquad.5Cqquad.5Cqquad.5C.3B.5C.3B_.5C.29_.C3.96vningar:_.C2.A0_Boken.2C_sid_218|<b><span style="color:blue">SVS</span></b>]]-struktur), ger cosinussatsen den tredje sidan som roten ur högerledet: <b><span style="color:red">endast en lösning</span></b>. | ||
| + | |||
| + | När två sidor är givna samt en vinkel som inte ligger mellan dem (icke-SVS-struktur) ger cosinussatsen en andragradsekvation som i regel har <b><span style="color:red">två lösningar</span></b>, se exemplet nedan. | ||
| + | |||
| + | <big><b><span style="color:#931136">Samma exempel som [[Kapitel_5_Trigonometri#Exempel_p.C3.A5_sinussatsen_.28tv.C3.A5_l.C3.B6sningar.29|<span style="color:blue">ovan</span>]], nu med cosinussatsen</span></b></big> | ||
| + | |||
| + | <div style="border:0px solid black;display:inline-table;margin-left: 10px;"> [[Image: 13 Ex Cosinussatsen_1_400.jpg]] </div><br> | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 13 Ex Cosinussatsen_2_400.jpg]] </div> | ||
| + | |||
| + | </td> | ||
| + | <td> </td> | ||
| + | <td> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <div class="ovnE"> | ||
| + | {{#NAVCONTENT:Varför två lösningar?|Varför två lösningar}} | ||
| + | </div> | ||
| + | |||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | Cosinussatsen ger samma två lösningar som sinussatsen, se [[Kapitel_5_Trigonometri#Exempel_p.C3.A5_sinussatsen_.28tv.C3.A5_l.C3.B6sningar.29|<b><span style="color:blue">ovan</span></b>]]. | ||
| + | |||
| + | |||
| + | == <b><span style="color:#931136">5.7 Användning av trigonometri <math> \qquad\qquad\;\; </math> <small><small>Övningar: Boken, sid 232-233 </small></small></span></b> == | ||
| + | <br> | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;">[[Image: 14 Spiraltrappa_750.jpg]]</div> | ||
| + | |||
| + | </td> | ||
| + | <td> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <div class="ovnE"> | ||
| + | {{#NAVCONTENT:Svar|5.7 Svar fel i 5.7}} | ||
| + | </div> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | |||
| + | <table> | ||
| + | <tr> | ||
| + | <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;">[[Image: 233 Uppg 4269 Femhorn 4270 Klippa-1_400.jpg]] </div> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | </td> | ||
| + | <td><div style="border:1px solid black;display:inline-table;margin-left: 20px;">[[Image: 233 Uppg 4269 Femhorn 4270 Klippa-2_400.jpg]] </div></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | |||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 10px;"> | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td>[[Image: 14_2_Balong_Uppg_450.jpg]] | ||
| + | |||
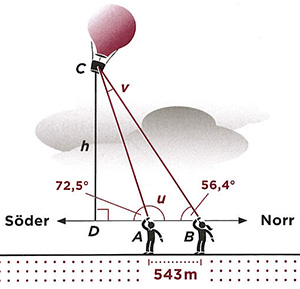
| + | ::<math> \underline{\rm Lösning:} \quad {\rm Vi\;ritar\;figuren\;till\;höger\;(modellering).} </math> | ||
| + | |||
| + | ::<math>{\rm Sidovinkeln} \quad u \, = \, 180^\circ - 72,5^\circ \, = \, 107,5^\circ </math> | ||
| + | |||
| + | ::<math>{\rm Vinkelsumman\;i\;triangeln\;} ABC {\rm \;ger} </math> | ||
| + | |||
| + | ::<math> v \, = \, 180^\circ - 56,4^\circ - 107,5^\circ\, = \, 16,1^\circ </math></td> | ||
| + | <td>[[Image: 14_2_Balong_Bild_300.jpg]]</td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | :[[Image: 14_2_Balong_Losning_450.jpg]]</div> | ||
| − | |||
| − | |||
</big> | </big> | ||
| Rad 155: | Rad 572: | ||
| − | [[Matte:Copyrights|Copyright]] © 2011- | + | [[Matte:Copyrights|Copyright]] © 2011-2019 Math Online Sweden AB. All Rights Reserved. |
Nuvarande version från 8 maj 2019 kl. 18.23
| << Förra kapitel | Kap 5 Trigonometri | Formelsamling Trigonometri | Planering Matte 3c | Diagnos kap 4-5 Integr. & Trigon. |
Detta kapitels övningar finns inte på webben (pga tidsbrist). Därför:
Läs igenom genomgångarna här, men använd för övningarna boken Matematik 5000.
Utdrag ur planeringen:
5.1 Trigonometri i rätvinkliga trianglar \( \qquad\;\; \) Övningar: Boken, sid 208
Tangens för \( \, v \, < \, 90^\circ \)
|
Flera exempel på tangens
|
|
Sinus och Cosinus för \( \, v \, < \, 90^\circ \)
5.2 Exakta trigonometriska värden / Enhetscirkeln \( \;\; \) Övningar: Boken, sid 209 / 210
Två speciella vinklar: \( \, 45^\circ \, \) och \( \, 60^\circ \, \)
Pythagoras satsen används på halva kvadraten med sidan \( \, 1 \, \) för att få diagonalen \( \, \sqrt{2} \). Sedan bestäms \( \, \sin 45^\circ \, \) och \( \, \tan 45^\circ \):
På liknande sätt används Pythagoras på halva liksidiga triangeln med sidan \( \, 2 \, \) för att få höjden \( \, \sqrt{3} \). Sedan bestäms \( \, \sin 60^\circ \) och \( \, \cos 60^\circ \).
"Exakt" betyder: Gå inte över till decimaltal, dvs:
- Bibehåll bråk med endast heltal i täljare och nämnare,
- Bibehåll rötter som inte ger heltal.
En konsekvens blir att inte ens rötter ska stå kvar i bråkens nämnare. Ta upp dem genom förlängning med \( \, \sqrt{{\color{White} {\cdots}}} \), t.ex.:
- \[ \displaystyle \frac{1}{\sqrt{2}} \, = \, \frac{1 \, \cdot \, {\color{Red} {\sqrt{2}}}}{\sqrt{2} \cdot {\color{Red} {\sqrt{2}}}} \, = \, \frac{\sqrt{2}}{2} \, = \, \frac{1}{2} \, \sqrt{2} \]
Ytterligare exakta trigonometriska värden
Andra geometriska satser ger följande exakta värden:
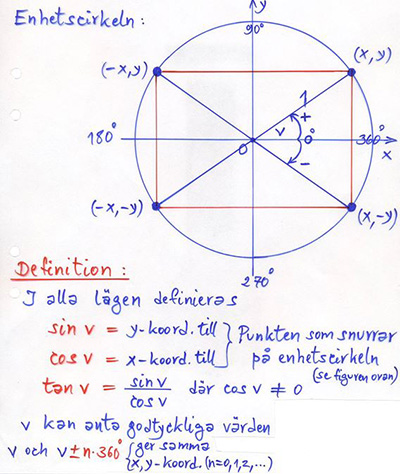
Enhetscirkeln
Cirkel \( \, = \, \) Mängden av alla punkter som har samma avstånd (radien \( \, r \, \)) från en punkt (medelpunkten \( \, M \, \)).
Cirkelns ekvation:
Enhetscirkeln är cirkeln med radien \( \, r \, = \, 1 \, \) och medelpunkten \( \, M \, = \, O \, \) (origo).
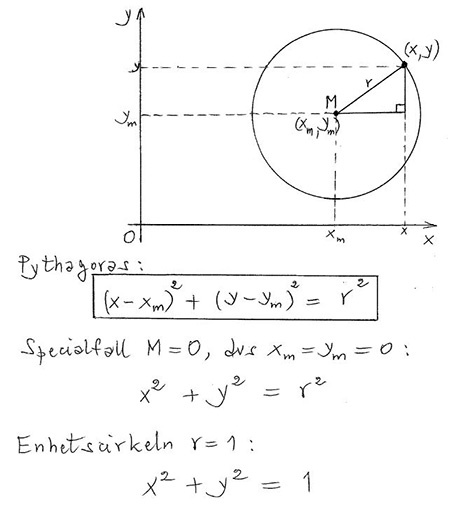
Om en punkt \( \, P\,(x, y) \, \) snurrar på enhetscirkeln och \( \, v \, \) är vinkeln mellan \( \, x\)-axeln och \( \, \overline{OP} \), så gäller:
| \( \qquad\qquad\quad \) |
\(\begin{array}{rcl} x & = & \cos v \\
y & = & \sin v
\end{array}\)
|
I cirklar med radien \( \, r \, > \, 1 \, \) förblir vinkeln \( \, v \, \) den samma och därmed \( \, \cos v = \displaystyle \frac{r \cdot \; x}{r} = x \, \) och \( \, \sin v = \displaystyle \frac{r \cdot \; y}{r} = y \), precis som ovan.
Detta används för att definiera de trigonometriska funktionerna i godtyckliga trianglar, dvs för vinklar \( \, v \, \geq \, 90^\circ \, \).
5.3 Godtyckliga trianglar \( \qquad\qquad\;\; \) Övningar: Boken, sid 215
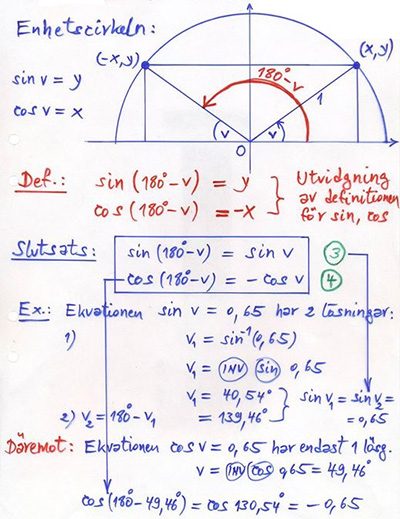
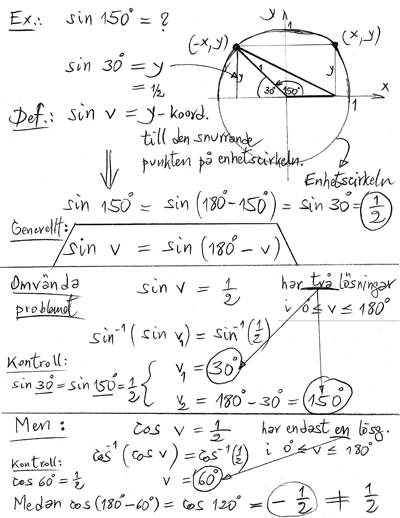
Sinus och Cosinus för vinklar i intervallet: \( \quad 90^\circ \, \leq \, v \, \leq \, 180^\circ \)
Exempel:
- \[ \sin 150^\circ \, = \, \sin (180^\circ - 30^\circ) \, = \, \sin 30^\circ \, = \, \frac{1}{2} \]
- \[ \cos 120^\circ \, = \, \cos (180^\circ - 60^\circ) \, = \, -\cos 60^\circ \, = \, -\frac{1}{2} \]
Förklaring med enhetscirkeln:
Punkten till vinkeln \( \, v \, \) har samma \( \, y\)-koordinat (\(=\sin v\)) som punkten till vinkeln \( \, 180-v \).
Punkten till vinkeln \( \, v \, \) har samma \( \, x\)-koordinat (\(=\cos v\)) som punkten till vinkeln \( \, 180-v \, \) med omvänt tecken.
| Ekvationer
med Sin & Cos:
|
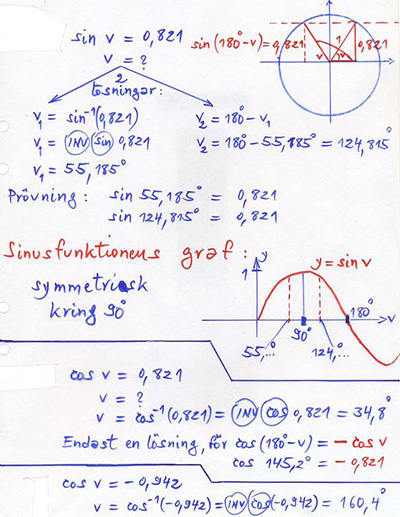
Sinus, Cosinus och Tangens för alla vinklar
|
|
En gång till
Sin & Cos för \( v \geq 90^\circ \) i trianglar:
|
|
En cosinusekvation har i intervallet \( \, 0^\circ \leq v \leq 180^\circ \, \) endast en lösning.
5.4 Triangelsatserna \( \qquad\qquad\qquad\;\; \) Övningar: Boken, sid 218
Det finns tre triangelsatser: Areasatsen, Sinussatsen och Cosinussatsen.
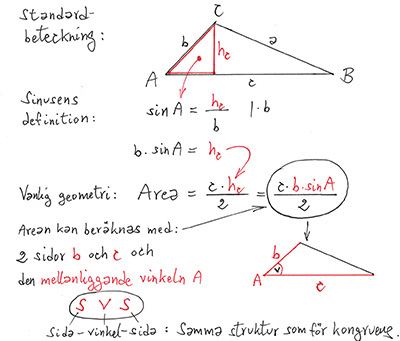
Triangelsatsernas formulering baseras på de standardbeteckningar för trianglar som införs här:
Areasatsen
Givet: \( \quad \) Två sidor och den mellanliggande vinkeln i en triangel.
Sökt: \( \quad\, \) Triangelns area.
|
|
Areasatsen i vanliga ord (utan beteckningar): En triangels area är produkten av två sidor
och den mellanliggande vinkelns sinus, delad med \( \, 2 \, \) (SVS-struktur). |
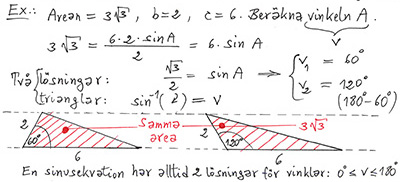
Det omvända problemet:
Givet: \( \quad \) Arean och två sidor av en triangel.
Sökt: \( \quad\, \) Den mellanliggande vinkeln \( \, v \, \).
|
Varför två lösningar?
|
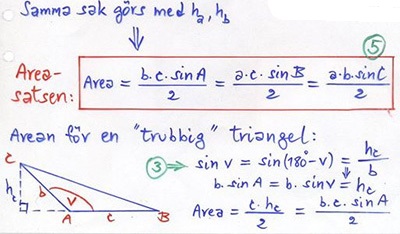
Det geometriska problemet har två lösningar. Areasatsen ger båda:
Areasatsen leder till en sinusekvation som pga sina två lösningar resulterar i två vinklar och därmed två trianglar.
5.5 Sinussatsen \( \qquad\qquad\qquad\;\; \) Övningar: Boken, sid 220 / 224-225
Givet: \( \quad \) Två sidor och en vinkel eller två vinklar och en sida i en triangel.
Sökt: \( \quad\, \) Triangelns tredje sida eller två andra sidor.
|
I en triangel är kvoten mellan
vinklarnas sinus och deras motstående sidor lika stor. |
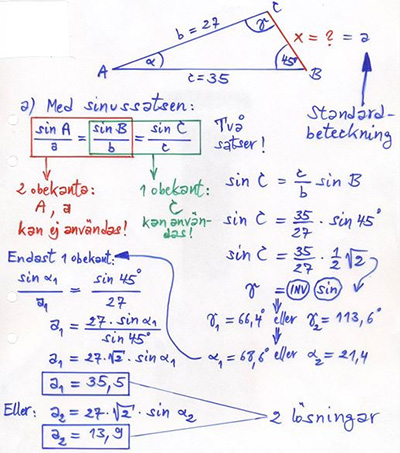
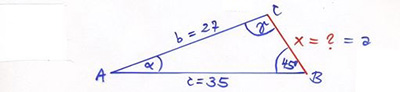
Exempel på sinussatsen (två lösningar)
Givet: \( \quad \) Två sidor och den vinkel som inte ligger mellan dem (icke-SVS-struktur).
Sökt: \( \quad\, \) Triangelns tredje sida.
|
|
Varför två lösningar?
|
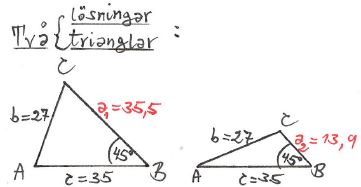
Att det finns två lösningar (två trianglar) beror på att problemet inte har SVS-struktur, dvs:
Triangelns två sidor \( \, b = 27 \, \) och \( \, c = 35 \, \) är givna, men inte den mellanliggande vinkeln, utan den som ligger mittemot \( \, b \).
5.6 Cosinussatsen \( \qquad\qquad\qquad\;\; \) Övningar: Boken, sid 229-230
Givet: \( \quad \) Två sidor och en vinkel i en triangel.
Sökt: \( \quad\, \) Triangelns tredje sida.
|
Cosinussatsen utvidgar Pythagoras med
en \( \cos\)-term som involverar högerledets två sidor och den mellanliggande vinkeln. |
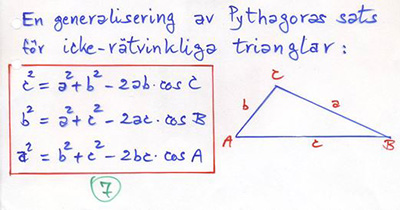
Pythagoras är ett specialfall av cosinussatsen för fallet: \( \; A , B , {\rm eller\;} C \, = \, 90^\circ \; \Rightarrow \; \cos 90^\circ \, = \, 0 \). Då försvinner \( \cos\)-termen i cosinussatsen.
När två sidor och den mellanliggande vinkeln i en triangel är givna (SVS-struktur), ger cosinussatsen den tredje sidan som roten ur högerledet: endast en lösning.
När två sidor är givna samt en vinkel som inte ligger mellan dem (icke-SVS-struktur) ger cosinussatsen en andragradsekvation som i regel har två lösningar, se exemplet nedan.
Samma exempel som ovan, nu med cosinussatsen
|
Varför två lösningar?
|
Cosinussatsen ger samma två lösningar som sinussatsen, se ovan.
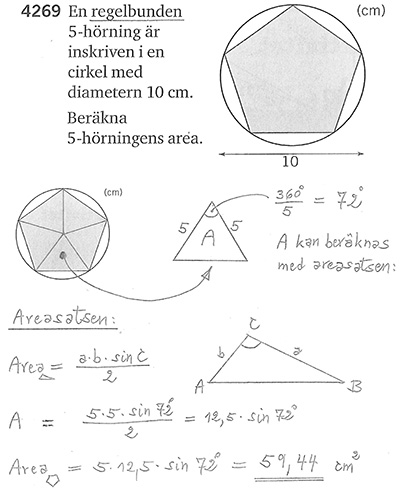
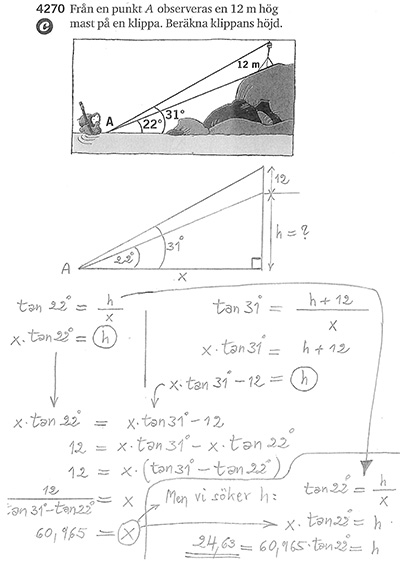
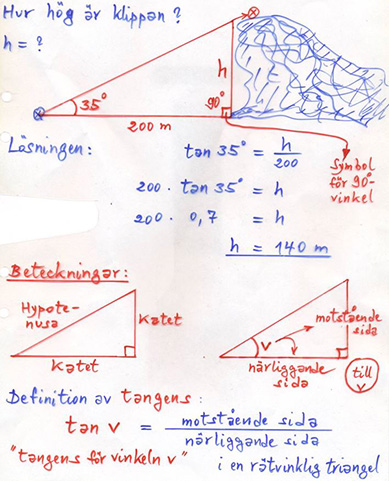
5.7 Användning av trigonometri \( \qquad\qquad\;\; \) Övningar: Boken, sid 232-233
|
Svar
|
|
|
Copyright © 2011-2019 Math Online Sweden AB. All Rights Reserved.


 Hämtar...
Hämtar...