Skillnad mellan versioner av "2.3 Fördjupning till Gränsvärde"

Från Mathonline
Hoppa till: navigering, sök
m
m
 
(33 mellanliggande versioner av samma användare visas inte)
Rad 10: Rad 10:
 
|}
 
|}
  
−
 
+
<!-- [[Media: Lektion_14_Gransvarde_Rutac.pdf|<b><span style="color:blue">Lektion 14 Gränsvärde</span></b>]] -->
−
[[Media: Lektion_14_Gransvarde_Rutab.pdf|<b><span style="color:blue">Lektion 14 Gränsvärde</span></b>]]
+
  
 
<big>
 
<big>
−
Vårt mål i detta kapitel är att definiera begreppet <b><span style="color:red">derivata</span></b>. Men eftersom derivata är ett gränsvärde, måste vi först veta vad gränsvärde är för något.
+
Vi förutsätter att alla funktioner <math> \, y = f(x) \, </math> i detta avsnitt är [[1.5_Kontinuerliga_och_diskreta_funktioner|<b><span style="color:blue">kontinuerliga</span></b>]] i sina resp. definitionsområden.
−
 
+
−
Förutsättning i detta avsnitt är att alla funktioner <math> \, y = f(x) \, </math> är [[1.5_Kontinuerliga_och_diskreta_funktioner|<b><span style="color:blue">kontinuerliga</span></b>]] för alla <math> \, x \, </math> av det betraktade området.
+
−
 
+
−
 
+
−
<big><b><span style="color:#931136">Exempel på gränsvärde</span></b></big> <!-- &nbsp; <b>Uppgift 3438 (3c-boken, sid 190):</b> -->
+
−
<table>
+
−
<tr>
+
−
<td><div class="ovnE0">
+
−
En fallskärmshoppare faller fritt med hastigheten
+
−
 
+
−
<math> \qquad\quad\;\;\; </math> <div class="smallBoxVariant"><math> v(t) = 80\,(1 - 0,88\,^t) </math></div>
+
−
 
+
−
där <math> \, t = \, </math> tiden i sek. Finns det en maximal hastighet
+
−
 
+
−
<math> \, v_{max} \, </math> som hopparen inte kan överskrida?
+
−
</div>
+
−
 
+
−
<b>Grafisk och fysikalisk tolkning:</b>
+
−
 
+
−
Grafen till <math> \, v(t) \, </math> visar att det finns en maximal hastighet <math> \, v_{max} = 80 </math> m/s <math> \;\; </math>
+
−
</td>
+
−
  <td>[[Image: 5 186 Uppg 3438 Fritt falla.jpg]]</td>
+
−
</tr>
+
−
</table>
+
−
som hopparen inte kan överskrida<span style="color:black">:</span> <math> \, v <  v_{max} </math>. Efter ca. 40 sek är <math> v \, \approx \, v_{max} \, </math> då hastigheten blir konstant <math> \, \approx 80 </math> m/s.
+
−
 
+
−
Enligt [https://www.naturvetenskap.org/fysik/gymnasiefysik/kraft/newtons-1a-lag/ <b><span style="color:blue">Newtons fösta lag</span></b>] är summan av alla krafter <math> \, = 0 \, </math> när ett föremål är i vila eller rör sig med konstant hastighet (och omvänt).
+
−
 
+
−
Därav följer<span style="color:black">:</span> <math> \qquad </math> Luftmotstånd <math> \, \approx \, </math> gravitation <math> \qquad </math> dvs <math> \qquad </math> rörelsen är ett fritt fall med luftmotstånd.
+
−
 
+
−
<b>Matematisk lösning:</b>
+
−
 
+
−
<div class="border-divblue"><math> </math><b><span style="color:red">Gränsvärdet</span></b>&nbsp; för <math> \, 80\,(1 - 0,88\,^t) \, </math>,&nbsp; då <math> \,t \, </math> går mot <math> \, \infty \; </math>,&nbsp; <b><span style="color:red">är <math> \, 80</math></span></b>&nbsp; .
+
−
 
+
−
Man skriver<span style="color:black">:</span> <math> \qquad \displaystyle {\color{Red} {\lim_{t \to \infty}}}\,{\left(80\,(1 - 0,88\,^t)\right)} {\color{Red} { \; = \; 80}} \qquad </math> och läser<span style="color:black">:</span>
+
−
 
+
−
<math> \qquad\;\; </math> Limes av <math> \, 80\,(1 - 0,88\,^t) \, </math>, då <math> t </math> går mot <math> \infty \, </math>, är <math> 80 </math>.
+
−
 
+
−
<math> {\color{Red} {\lim}} \, </math> står för det latinska ordet <math> \, {\color{Red} {\rm limes}} \, </math> som betyder gräns.
+
−
</div>
+
−
 
+
−
<b>Limes kan beräknas:</b>
+
−
 
+
−
<math> v_{max} \, = \, \displaystyle \lim_{t \to \infty}\,{(80\,(1 - 0,88\,^t))} \, = \, \lim_{t \to \infty}\,{(80 - 80\cdot0,88\,^t)} \, = \, \lim_{t \to \infty}\,{80} - \lim_{t \to \infty}\,{(80\cdot0,88\,^t)} \, = \, 80 \, - \, 0 \, = \, 80 \, </math>,
+
−
 
+
−
eftersom <math> \qquad\;\; \displaystyle \lim_{t \to \infty}\,{(80\cdot0,88\,^t)} \, = \, \lim_{t \to \infty}\,{80} \cdot \lim_{t \to \infty}\,{(0,88\,^t)} \, = \, 80 \cdot 0 \, = \, 0 \quad </math> pga <math> \quad 0,88 \, < \, 1 \; </math>.
+
  
 
=== <b><span style="color:#931136">Gränsvärde för en funktion</span></b> ===
 
=== <b><span style="color:#931136">Gränsvärde för en funktion</span></b> ===
−
 
 
<div class="exempel">
 
<div class="exempel">
 
==== <b><span style="color:#931136">Exempel</span></b> ====
 
==== <b><span style="color:#931136">Exempel</span></b> ====
  
−
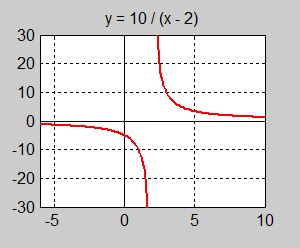
Funktionen <math> y = f(x) = \displaystyle {10 \over x\,-\,2} </math> är given<span style="color:black">:</span> <math> \qquad\qquad </math> <b><span style="color:red">Vad händer med <math> \, y \, </math> när <math> \; x \to \infty \; </math>?</span></b>
+
Funktionen <math> y = f(x) = \displaystyle {10 \over x\,-\,2} </math> är given.
 
<table>
 
<table>
 
<tr>
 
<tr>
 
   <td><math> \quad </math>[[Image: Ex 1 Gransvarde.jpg]]</td>
 
   <td><math> \quad </math>[[Image: Ex 1 Gransvarde.jpg]]</td>
 
<td><math> \quad </math></td>
 
<td><math> \quad </math></td>
−
   <td><div class="border-divblue"><b><span style="color:red">Gränsvärdet</span></b>&nbsp; för <math> \, \displaystyle {10 \over x\,-\,2} \, </math>,&nbsp; då <math> \,x \, </math> går mot <math> \, \infty \; </math>,&nbsp;  <b><span style="color:red">är <math> \, 0</math></span></b> &nbsp;<span style="color:black">:</span>
+
   <td><b><span style="color:red">Vad händer med <math> \, y \, </math> när <math> \; x \to \infty \; </math>?</span></b>
 +
<br>
 +
<div class="border-divblue8"><small><b><span style="color:red">Gränsvärdet</span></b>&nbsp; för <math> \, \displaystyle {10 \over x\,-\,2} \, </math>,&nbsp; då <math> \,x \, </math> går mot <math> \, \infty \; </math>,&nbsp;  <b><span style="color:red">är <math> \, 0</math></span></b> &nbsp;<span style="color:black">:</span>
  
  
 
<math> \quad\qquad\qquad\qquad\, \displaystyle {\color{Red} {\lim_{x \to \infty}}}\,{10 \over x\,-\,2} {\color{Red} { \; = \; 0}} </math>
 
<math> \quad\qquad\qquad\qquad\, \displaystyle {\color{Red} {\lim_{x \to \infty}}}\,{10 \over x\,-\,2} {\color{Red} { \; = \; 0}} </math>
−
</div>
+
</small></div>
−
 
+
  
 
'''Grafiskt''':&nbsp; Kurvan närmar sig <math> \, x </math>-axeln när <math> \, x \, </math> växer, dvs <math> \, y\, </math> blir allt mindre ju större <math> \, x \, </math> blir.
 
'''Grafiskt''':&nbsp; Kurvan närmar sig <math> \, x </math>-axeln när <math> \, x \, </math> växer, dvs <math> \, y\, </math> blir allt mindre ju större <math> \, x \, </math> blir.
Rad 85: Rad 38:
 
</tr>
 
</tr>
 
</table>
 
</table>
−
'''Analytiskt''':&nbsp; Ekvationen <math> \, \displaystyle {10 \over x\,-\,2} \, = \, 0 \, </math> saknar lösning, därför att täljaren <math> \, 10\, </math> är en konstant som aldrig kan bli <math> \, 0 </math>. Så kan inte heller hela uttrycket i vänsterled bli <math> \, 0 \, </math> oavsett <math> \, x </math>. Nämnaren växer däremot obegränsat när <math> \, x \, </math> växer. Därför går hela uttrycket i vänsterled mot <math> \, 0 </math>.
+
'''Analytiskt''':&nbsp; Ekvationen <math> \, \displaystyle {10 \over x\,-\,2} \, = \, 0 \, </math> saknar lösning, därför att täljaren <math> \, 10\, </math> är en konstant som aldrig kan bli <math> \, 0 </math>. Så kan inte heller <math> \, \displaystyle {10 \over x\,-\,2} \, </math> bli <math> \, 0 \, </math>, oavsett <math> \, x </math>. Nämnaren växer däremot obegränsat när <math> \, x \, </math> växer. Konstant delad med  obegränsat växande värden går mot <math> \, 0 \, </math>. Man skriver<span style="color:black">:</span>
  
−
Man säger<span style="color:black">:</span> <math> \; \displaystyle {10 \over x\,-\,2} \; {\rm går\;mot} \, 0 \; {\rm när} \; x \; {\rm går\;mot} \, \infty \, </math>, kort<span style="color:black">:</span> <math> \;\; \displaystyle {10 \over x\,-\,2} \to 0 \quad {\rm när} \quad x \to \infty \;\; </math>, bättre uttryckt<span style="color:black">:</span> <math> \, \boxed{ \displaystyle \lim_{x \to \infty}\,{10 \over x\,-\,2} \, = \, 0} \, </math>.
+
<math> \displaystyle {10 \over x\,-\,2} \to 0 \quad {\rm när} \quad x \to \infty \;\; </math>, bättre uttryckt<span style="color:black">:</span> <math> \, \boxed{ \displaystyle \lim_{x \to \infty}\,{10 \over x\,-\,2} \, = \, 0} \, </math>. Av samma anledning är<span style="color:black">:</span> <math> \, \boxed{ \displaystyle \lim_{x \to \infty}\,{1 \over x} \, = \, 0} \, </math>.
  
 
<b><span style="color:red">Vad händer med <math> \, y \, </math> när <math> \; x \to - \infty \; </math>?</span></b>
 
<b><span style="color:red">Vad händer med <math> \, y \, </math> när <math> \; x \to - \infty \; </math>?</span></b>
Rad 93: Rad 46:
 
Något liknande visas när <math> \, x \, </math> går mot negativa värden, dvs när <math> x \to \, {\color{Red} {- \infty}} </math>: &nbsp; <math> \,y\, </math> mot <math> \,0\, </math> bara att <math> \, y\, </math> nu närmar sig <math> \, 0 \, </math> nedifrån, kort<span style="color:black">:</span> <math> \;\; y \to 0 \quad {\rm när} \quad x \to {\color{Red} {- \infty}} \; </math>.  
 
Något liknande visas när <math> \, x \, </math> går mot negativa värden, dvs när <math> x \to \, {\color{Red} {- \infty}} </math>: &nbsp; <math> \,y\, </math> mot <math> \,0\, </math> bara att <math> \, y\, </math> nu närmar sig <math> \, 0 \, </math> nedifrån, kort<span style="color:black">:</span> <math> \;\; y \to 0 \quad {\rm när} \quad x \to {\color{Red} {- \infty}} \; </math>.  
 
</div>
 
</div>
−
 
  
 
"Paradoxen" att funktionen allt mer närmar sig <math> \, 0 \, </math> utan att någonsin bli <math> \, 0 </math>, löses upp och kan därmed hanteras analytiskt med hjälp av <b><span style="color:red">limes</span></b> som generellt beskriver fenomenet att närma sig ett värde allt mer utan att nå det någonsin.  
 
"Paradoxen" att funktionen allt mer närmar sig <math> \, 0 \, </math> utan att någonsin bli <math> \, 0 </math>, löses upp och kan därmed hanteras analytiskt med hjälp av <b><span style="color:red">limes</span></b> som generellt beskriver fenomenet att närma sig ett värde allt mer utan att nå det någonsin.  
  
−
Limesbegreppet är centralt inom <b><span style="color:red">Analys</span></b><math>-</math> den gren av matematiken som [https://sv.wikipedia.org/wiki/Isaac_Newton <b><span style="color:blue">Newton</span></b>] och [https://sv.wikipedia.org/wiki/Gottfried_Wilhelm_von_Leibniz <b><span style="color:blue">Leibniz</span></b>] på 1700-talet la grunden till, även kallad <b><span style="color:red">Differential- och Integralkalkyl</span></b>, på engelska <b><span style="color:red">Calculus</span></b>. Det är därför vi numera använder begreppet "analytiskt" istället för "algebraiskt".
 
  
−
I detta kapitel kommer vi att använda limes för att definiera derivatan analytiskt som ett gränsvärde. För att kunna göra det måste vi lära oss att <b><span style="color:red">beräkna</span></b> gränsvärden.
+
=== <b><span style="color:#931136">Existens av gränsvärden</span></b> ===
−
</big>
+
  
 +
I exemplet ovan bestämdes <math> \, \displaystyle \lim_{x \to \infty}\,{10 \over x\,-\,2} \, </math> utan att fråga om gränsvärdet överhuvudtaget ''existerade''. Att gränsvärdet sedan blev <math> \, 0 \, </math> bevisade ju existensen. Men det finns faktiskt fall där ett gränsvärde ''inte'' existerar och därför inte heller kan bestämmas. Det vore bra om man kunde undersöka det innan man började räkna.
  
−
== <b><span style="color:#931136">Beräkning av gränsvärden</span></b> ==
+
Som exempel tar vi samma funktion som ovan, men betraktar dess beteende för <math> \; \color{Red} {x \to 2} \; </math>. 
  
−
<big>
+
<div class="exempel">
−
I princip kan limes av en funktion beräknas genom att sätta in i funktionsuttrycket det värde som <math> \,x \, </math> ska gå emot. Men ofta ger detta odefinierade uttryck.
+
==== <b><span style="color:#931136">Exempel på att gränsvärde saknas</span></b> ====
  
−
Därför måste man först <b><span style="color:red">förenkla uttrycket</span></b>, ev. flera gånger. Sedan sätts in det värde som <math> \,x \, </math> ska gå emot, i funktionsuttrycket.
+
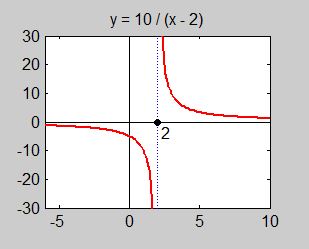
Funktionen <math> y = f(x) = \displaystyle {10 \over x\,-\,2} </math> är given<span style="color:black">:</span> <math> \qquad\qquad\qquad </math> <b><span style="color:red">Vad händer med <math> \, y \, </math> när <math> \; x \to 2 \; </math>?</span></b>
−
</big>
+
<table>
 +
<tr>
 +
  <td>Bestäm <math> \quad \displaystyle \lim_{\color{Red} {x \to 2}}\,{10 \over x\,-\,2} </math>
  
 +
'''Svar:''' <math> \quad\;\; f(x)\, </math> är inte definierad för <math> x = 2\, </math>.
  
−
<div class="ovnE">
+
<math> \qquad\qquad\qquad\qquad\quad \Downarrow </math>
−
==== <b><span style="color:#931136">Exempel 1</span></b> ====
+
  
−
Bestäm <math> \qquad \displaystyle \lim_{x \to 0}\, {x^2 + 7\,x \over x} </math>
+
<div class="border-divblue"><math> \displaystyle \lim_{\color{Red} {x \to 2}}\,{10 \over x\,-\,2} \quad </math> <b>existerar inte</b>&nbsp;&nbsp;&nbsp;<span style="color:black">:</span>  
  
−
<b>Lösning:</b>
 
−
 
−
För <math> \, x = 0 \, </math> är uttrycket <math> \, \displaystyle{x^2 + 7\,x \over x} \, </math> inte definierat därför att nämnaren blir <math> \, 0 </math>.
 
−
 
−
Därför måste vi förenkla uttrycket.
 
−
 
−
Vi faktoriserar uttryckets täljare för att kolla om man ev. kan förkorta.
 
−
 
−
Täljaren kan faktoriseras genom att bryta ut <math> x \, </math>:
 
  
−
::<math> \lim_{x \to 0}\, {x^2 + 7\,x \over x} \, = \, \lim_{x \to 0}\, {{\color{Red} x}\:(x + 7) \over {\color{Red} x}} \, = \, \lim_{x \to 0}\, (x + 7) \, = \, 0 + 7 \, = \, 7 </math>
+
<math> \qquad </math> <b><span style="color:red">Gränsvärde saknas.</span></b>
 
</div>
 
</div>
 +
</td>
 +
  <td><math> \qquad </math></td>
 +
  <td>[[Image: Ex 2 Gransvarde.jpg]]</td>
 +
</tr>
 +
</table>
  
 +
Grafen visar att kurvan skjuter upp i höjden å ena sidan och ner i "djupet" å andra sidan av punkten <math> \, x = 2 </math>.
  
−
<div class="ovnE">
+
Algebraiskt är <math> \, f(x)\, </math> inte definierad för <math> x = 2\, </math>, för <math> \displaystyle{10 \over x\,-\,2} </math>:s nämnare blir <math> \, 0\, </math> för <math> \, x = 2 </math>.
−
==== <b><span style="color:#931136">Exempel 2</span></b> ====
+
  
−
Bestäm <math> \qquad \displaystyle \lim_{x \to \infty}\, {4\,x\,+\,5 \over x} </math>
+
Dessutom finns det två olika resultat beroende på om <math> \, x </math> går mot <math> \, 2 </math> från höger eller från vänster<span style="color:black">:</span>  
  
−
<b>Lösning:</b>
+
<math> f(x)\, </math> går mot <math> +\, \infty </math> när man närmar sig <math> \, x = 2 </math> från höger och mot <math> -\, \infty </math> när man närmar sig <math> \, x = 2 </math> från vänster.
  
−
Vi förenklar uttrycket i limes genom att separera summan i uttrycket:
+
<math> y \;\; {\rm går\;mot} \, +\infty \; {\rm när} \; x \; {\rm går\;mot} \, 2 \;{\rm från\;höger:} \; \qquad\quad y \to +\infty \quad {\rm när} \quad x \to 2^+ </math>
  
−
::<math> {4\,x\,+\,5 \over x} = {4\,{\color{Red} x} \over {\color{Red} x}} \,+\,{5 \over x} \,=\, 4 \,+\, {5 \over x} </math>
+
<math> y \;\; {\rm går\;mot} \, -\infty \; {\rm när} \; x \; {\rm går\;mot} \, 2 \;{\rm från\;vänster:} \; \qquad\; y \to -\infty \quad {\rm när} \quad x \to 2^- </math>
  
−
<math> \displaystyle{5 \over x} </math> går mot <math> 0 </math><span style="color:black">:</span> <math> \qquad \displaystyle \lim_{x \to \infty}\, {5 \over x} \, = \, 0 </math>
+
där <math> x \to 2^+ </math> betyder att närma sig <math> \, x = 2 </math> från höger (<math> \, x > 2 </math>) och <math> x \to 2^- </math> att närma sig <math> \, x = 2 </math> från vänster (<math> \, x < 2 </math>).
 +
</div>
  
−
Därför kan vi bestämma limes för hela uttrycket:
 
  
−
::<math> \lim_{x \to \infty}\, {4\,x\,+\,5 \over x} \, = \, \lim_{x \to \infty}\, \left(4 \,+\, {5 \over x}\right) \,= \, 4\,+\,0 \,= \, 4 \;\, </math>
+
Följande modifierad variant av [[2.3_Gränsvärde#Exempel_2|<b><span style="color:blue">Exempel 2</span></b>]] (<math> \, {\color{Red} {x \to 0}} \, </math> istället för <math> \, x \to \infty </math>) är ytterligare ett exempel på att gränsvärdet saknas:
−
</div>
+
</big>
  
  
 
<div class="ovnE">
 
<div class="ovnE">
−
==== <b><span style="color:#931136">Exempel 3</span></b> ====
 
  
−
Bestäm <math> \qquad \displaystyle \lim_{x \to 2}\, {x^2\,-\,4 \over 5\,x - 10} </math>
+
==== <b><span style="color:#931136">Exempel 2 a</span></b> ====
  
−
<b>Lösning:</b>
+
Bestäm <math> \qquad \displaystyle \lim_{x \to 0}\, {4\,x\,+\,5 \over x} </math>
−
 
+
−
Insättningen av <math> \, x = 2 \, </math> i uttrycket ger det odefinierade uttrycket <math> \, \displaystyle{0 \over 0} </math>.
+
−
 
+
−
Vi faktoriserar både täljaren och nämnaren för att kolla om man ev. kan förkorta.
+
−
 
+
−
Täljaren kan faktoriseras med hjälp av konjugatreglen och nämnaren genom att bryta ut:
+
−
 
+
−
::<math> x^2\,-\,4 = (x\,+\,2)\cdot(x\,-\,2) </math>
+
−
 
+
−
::<math> 5\,x - 10 = 5\,(x\,-\,2) </math>
+
−
 
+
−
Nu kan vi förkorta uttrycket och beräkna limes:
+
−
 
+
−
::<math> \lim_{x \to 2}\, {x^2\,-\,4 \over 5\,x - 10} \, = \, \lim_{x \to 2}\, {(x + 2) \cdot {\color{Red} {(x-2)}} \over 5\,{\color{Red} {(x-2)}}} \, = \, \lim_{x \to 2} \, {x + 2 \over 5} \, = \, {2 + 2 \over 5} \, = \, {4 \over 5} \, = \, 0,8 </math>
+
−
</div>
+
−
 
+
−
 
+
−
<div class="ovnC">
+
−
==== <b><span style="color:#931136">Exempel 4</span></b> ====
+
−
 
+
−
Bestäm <math> \qquad \displaystyle \lim_{x \to 3}\, {x^2 - x - 6 \over x - 3} </math>
+
  
 
<b>Lösning:</b>
 
<b>Lösning:</b>
  
−
Insättningen av <math> \, x = 3 \, </math> i uttrycket ger det odefinierade uttrycket <math> \, \displaystyle{0 \over 0} </math>.
+
::<math> \lim_{x \to 0^+}\, {4\,x\,+\,5 \over x} \, = \, \lim_{x \to 0^+}\, \left(4 \,+\, {5 \over x}\right) \,= \, +\infty </math>
−
 
+
−
För att kunna se om man ev. kan förkorta uttrycket faktoriserar vi täljaren:
+
−
 
+
−
::<math> x^2 - x - 6 = 0 \, </math>
+
−
 
+
−
<math>p</math>-<math> q</math>-formeln kan användas, men enligt [[1.2_Repetition_Faktorisering_%26_Vieta_från_Matte_2#Vietas_formler_-_samband_mellan_koefficienter_och_nollst.C3.A4llen|<b><span style="color:blue">Vieta</span></b>]] gäller för lösningarna <math> \, x_1\,</math> och <math> \, x_2 \, </math> (går snabbare) <span style="color:black">:</span>
+
−
 
+
−
::<math> \begin{align} x_1  +   x_2 & = -(-1) = 1  \\
+
−
                      x_1 \cdot x_2 & = - 6
+
−
          \end{align}</math>
+
−
 
+
−
Två tal vars produkt är <math> \, -6 \, </math> är t.ex. <math> \, 3 \, </math> och <math> \, -2 </math>. Men även deras summa är <math> \, 1 </math>. Därför:
+
−
 
+
−
::<math> \begin{align} x_1 & = 3  \\
+
−
                      x_2 & = - 2
+
−
          \end{align}</math>
+
  
−
Täljarens faktorisering blir då:
+
::<math> \lim_{x \to 0^-}\, {4\,x\,+\,5 \over x} \, = \, \lim_{x \to 0^-}\, \left(4 \,+\, {5 \over x}\right) \,= \, -\infty </math>
  
−
::<math> x^2 - x - 6 = (x - 3) \cdot (x + 2) </math>
+
där <math> x \to 0^+ </math> betyder att närma sig <math> \, x = 0 </math> från höger (<math> \, x > 0 </math>) och <math> x \to 0^- </math> att närma sig <math> \, x = 0 </math> från vänster (<math> \, x < 0 </math>).
  
−
Nu kan vi förkorta uttrycket mot nämnaren och beräkna limes:
+
<b>Anmärkning:</b> Sättet att skriva limes som ovan förklaras nedan i [[2.3_Fördjupning_till_Gränsvärde#Ensidiga_och_oegentliga_gr.C3.A4nsv.C3.A4rden|<b><span style="color:blue">Ensidiga och oegentliga gränsvärden</span></b>]].
  
−
::<math> \lim_{x \to 3}\, {x^2 - x - 6 \over x - 3} \, = \, \lim_{x \to 3}\, {{\color{Red} {(x-3)}} \cdot (x + 2) \over {\color{Red} {(x-3)}}} \, = \, \lim_{x \to 3}\, (x + 2) \, = \, 3 + 2 \, = \, 5 </math>
+
<b>Svar:</b> <math> \qquad\;\; </math> Gränsvärde saknas.
 
</div>
 
</div>
  
  
−
<div class="ovnC">
+
<big>
−
==== <b><span style="color:#931136">Exempel 5</span></b> ====
+
Men även om en funktion skulle gå mot t.ex. mot <math> +\,\infty </math>, för ett visst <math> \, x </math> både från höger och vänster, t.ex. <math> \displaystyle {f(x) = {1 \over x^2}} </math> för <math> \, x = 0 </math>, skulle det strikt matematiskt inte vara korrekt att säga att limes existerar och är <math> +\,\infty </math>, därför att <math> \infty </math> inte är något värde. Med andra ord: 
  
−
Bestäm <math> \qquad \displaystyle \lim_{x \to \infty}\,\, {x^3\,-\,2 \over 2\,x^3\,+\,3\,x\,-\,4} </math>
 
  
−
<b>Lösning:</b>
+
<div class="border-divblue">Ett gränsvärde måste, för att existera, vara både entydigt och ändligt.</div>
  
−
För att förenkla uttrycket i limes divideras uttryckets täljare och nämnare med den högsta <math> \,x</math>-potensen, nämligen med <math> \,x^3 </math>:
 
  
−
::<math> \lim_{x \to \infty}\,\, {x^3\,-\,2 \over 2\,x^3\,+\,3\,x\,-\,4} \,=\, \lim_{x \to \infty}\,\, {x^3/x^3\,-\,2/x^3 \over 2\,x^3/x^3\,+\,3\,x/x^3\,-\,4/x^3} \,=\, \lim_{x \to \infty}\,\, {1\,-\,{\color{Red} {2/x^3}} \over 2\,+\,{\color{Blue} {3/x^2}}\,-\,{\color{ForestGreen} {4/x^3}}} </math>
+
Därför är det matematiskt korrekt att säga: Gränsvärdena <math> \; \displaystyle {\lim_{x \to 2}\,{10 \over x - 2}} \; </math> och <math> \; \displaystyle {\lim_{x \to 0}\,{1 \over x^2}} \;</math> existerar inte.
−
 
+
</big>
−
 
+
−
För att förenkla sista uttrycket använder vi:
+
−
 
+
−
::<math> \lim_{x \to \infty}\, {\color{Red} {2 \over x^3}} \, = \, \lim_{x \to \infty}\, {\color{Blue} {3 \over x^2}} \, = \, \lim_{x \to \infty} \, {\color{ForestGreen} {4 \over x^3}} \, = \, 0 </math>
+
−
 
+
−
Insatt i det sista uttrycket blir det:
+
−
 
+
−
::<math> \lim_{x \to \infty}\,\, {x^3\,-\,2 \over 2\,x^3\,+\,3\,x\,-\,4} \,=\quad \cdots \quad = \, \lim_{x \to \infty}\,\, {1\,-\,{\color{Red} {2/x^3}} \over 2\,+\,{\color{Blue} {3/x^2}}\,-\,{\color{ForestGreen} {4/x^3}}} \,=\, {1\,-\,{\color{Red} 0} \over 2\,+\,{\color{Blue} 0}\,-\,{\color{ForestGreen} 0}} \,=\, {1 \over 2} </math>
+
−
</div>
+
  
  
 
<div class="ovnA">
 
<div class="ovnA">
−
==== <b><span style="color:#931136">Exempel 6</span></b> ====
+
=== <b><span style="color:#931136">Ensidiga och oegentliga gränsvärden</span></b> ===
  
−
Funktionen <math> \; f(x) = x^2 \; </math> är given. &nbsp; Bestäm gränsvärdet <math> \quad \displaystyle \lim_{h \to 0}\,\,{f(2+h) - f(2) \over h} \; </math>.
+
Skiljer man närmandet från höger till <math> \, x = 2 \, </math> från närmandet från vänster kan man bilda s.k. <b><span style="color:red">ensidiga gränsvärden</span></b>:
  
−
<b>Lösning:</b>
+
:::<math> \lim_{x \to 2^{+}}\,{10 \over x - 2}\,=\,+\,\infty \qquad\quad \; {\rm och} \; \qquad\quad \lim_{x \to 2^{-}}\,{10 \over x - 2}\,=\,-\,\infty </math>
  
−
::<math> f(2+h) \, = \, (2+h)\,^2 \, = \, {\color{Red} {4 + 4\,h + h\,^2}} </math>
+
där <math> x \to 2^+ </math> betyder att närma sig <math> \, x = 2 </math> från höger (<math> \, x > 2 </math>) och <math> x \to 2^- </math> att närma sig <math> \, x = 2 </math> från vänster (<math> \, x < 2 </math>).
  
−
::<math> f(2) \, = \, 2\,^2 \, = \, {\color{Blue} 4} </math>
+
Man pratar om höger- och vänstergränsvärdet genom att skilja mellan de två sätten att närma sig talet <math> \, 2 </math> på <math> \, x</math>-axeln: från höger <math> x \to 2^+ </math> och från vänster <math> x \to 2^- </math>, därav beteckningen <b><span style="color:red">ensidig</span></b>. I vårt exempel ger de också två olika resultat.
  
−
::<math> \lim_{h \to 0}\,\,{f(2+h) - f(2) \over h} \, = \, \lim_{h \to 0} {{\color{Red} {4 + 4\,h + h\,^2}}\,\,-\,\,{\color{Blue} 4} \over h} = \lim_{h \to 0} {4\,h + h^2 \over h} = </math>
+
Gränsvärden av funktioner som går mot oändligheten (och därmed strikt talat inte existerar), men ändå skrivs med limessymbolen, kallar man <b><span style="color:red">oegentliga gränsvärden</span></b>.
  
−
::<math> = \lim_{h \to 0} {{\color{Red} h}\,(4 + h) \over {\color{Red} h}} = \lim_{h \to 0} \, (4 + h) = 4 </math>
+
<div class="exempel">
−
</div>
+
==== <b><span style="color:#931136">Exempel</span></b> ====
 +
<table>
 +
<tr>
 +
  <td>
  
 +
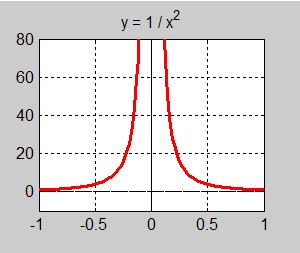
<math> \qquad\qquad\qquad\qquad\qquad \displaystyle {\lim_{x \to 0}\,{1 \over x^2}}\,=\,+\,\infty </math>
  
−
<div class="ovnA">
 
−
==== <b><span style="color:#931136">Exempel 7</span></b> ====
 
  
−
Funktionen <math> \; f(x) = x^2 \; </math> är given. &nbsp; Bestäm gränsvärdet <math> \quad \displaystyle \lim_{h \to 0}\,\,{f(x+h) - f(x) \over h} \; </math>.
+
Grafen visar att funktionen <math> \displaystyle f(x) = {1 \over x^2} </math> går mot <math> +\,\infty </math> både
  
−
<b>Lösning:</b>
+
när <math> \, x \to 0 </math> från höger (<math> \, x > 0 </math>) och från vänster (<math> \, x < 0 </math>). Visserligen
  
−
Eftersom uttrycket i limes involverar två variabler <math> \, x \, </math> och <math> \, h \, </math> kommer limes inte längre vara ett tal utan ett uttryck i <math> \, x </math>.
+
är gränsvärdet entydigt, men det är oändligt och kallas därför <b><span style="color:red">oegentligt</span></b>.
  
−
<math> \displaystyle \lim_{\color{Red} {h \to 0}} \, </math> innebär att gränsvärdet ska bildas för <math> \, {\color{Red} {h \to 0}} </math>. Därför borde <math> \, x\, </math> under gränsprocessen anses som en konstant.
 
  
−
::<math> {\color{Red} {f(x+h)}} \, = \, (x+h)^2 \, = \, {\color{Red} {x^2 + 2\,x\,h + h^2}} </math>  
+
Däremot är <math> \displaystyle \lim_{x \to 2}\,{10 \over x - 2} </math> varken entydigt eller ändligt. Därför existerar det inte.
 +
</td>
 +
  <td><math> \qquad </math></td>
 +
  <td>[[Image: y = 1 genom x^2.jpg]]</td>
 +
</tr>
 +
</table>  
  
−
::<math> {\color{Blue} {f(x)}} \, = \, {\color{Blue} {x\,^2}} </math>
+
Att man använder det ovannämnda skrivsättet för ensidiga och oegentliga gränsvärden sker av praktiska skäl. Man ersätter pilarna som vi använde inledningsvis med att beskriva gränsprocessen med limessymbolen istället. Det är bekvämt att använda en enhetlig notation för att beskriva gränsprocesser. Är man medveten om att limes enligt den strikta definitionen inte existerar, är det o.k.
  
−
::<math> \lim_{h \to 0}\,\,{{\color{Red} {f(x+h)}} - {\color{Blue} {f(x)}} \over h} \, = \, \lim_{h \to 0} {{\color{Red} {x^2 + 2\,x\,h + h^2}} \, - \, {\color{Blue} {x\,^2}} \over h} \, = \, \lim_{h \to 0} {2\,x\,h + h^2 \over h} = </math>
+
OBS! Av skrivsättet för ensidiga och oegentliga gränsvärden följer fortfarande <b><span style="color:red">inte</span></b> att <math> \; \displaystyle {\lim_{x \to 2}\,{10 \over x - 2}} \; </math> eller <math> \; \displaystyle {\lim_{x \to 0}\,{1 \over x^2}} \; </math> <b><span style="color:red">existerar</span></b>.
 +
</div>
  
−
::<math> = \lim_{h \to 0} {{\color{Red} h}\,(2\,x + h) \over {\color{Red} h}} = \lim_{h \to 0} \, (2\,x + h) =  \boxed{2\,x} </math>
 
  
−
Observera att <b><span style="color:#931136">Exempel 6</span></b> ovan är ett specialfall av detta exempel för <math> x = 2 \, </math>.
 
−
 
−
Jämför även med förra avsnittets [[2.2_Genomsnittlig_förändringshastighet#Exempel_2_Kvadratisk_funktion|<b><span style="color:blue">Exempel 2 Kvadratisk funktion</span></b>]]<span style="color:black">:</span>
 
−
 
−
<math> y \, = \, \boxed{2\,x} \, </math> är derivatan av <math> \, y \, = \, x^2 \, </math>, se [[2.4_Derivatans_definition#Derivatan_som_en_ny_funktion|<b><span style="color:blue">derivatan som en ny funktion</span></b>]].
 
 
</div>
 
</div>
  
Rad 281: Rad 182:
  
 
https://www.youtube.com/watch?v=fPOX0QX8AH0
 
https://www.youtube.com/watch?v=fPOX0QX8AH0
−
</big>
 
  
  
Rad 292: Rad 192:
  
  
−
[[Matte:Copyrights|Copyright]] © 2011-2017 Taifun Alishenas. All Rights Reserved.
+
[[Matte:Copyrights|Copyright]] © 2020 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved.

Nuvarande version från 2 maj 2020 kl. 21.19

        <<  Förra avsnitt          Genomgång          Övningar          Fördjupning          Nästa avsnitt  >>      


Vi förutsätter att alla funktioner \( \, y = f(x) \, \) i detta avsnitt är kontinuerliga i sina resp. definitionsområden.

Gränsvärde för en funktion

Exempel

Funktionen \( y = f(x) = \displaystyle {10 \over x\,-\,2} \) är given.

\( \quad \)Ex 1 Gransvarde.jpg \( \quad \) Vad händer med \( \, y \, \) när \( \; x \to \infty \; \)?


Gränsvärdet  för \( \, \displaystyle {10 \over x\,-\,2} \, \),  då \( \,x \, \) går mot \( \, \infty \; \),  är \( \, 0\)  :


\( \quad\qquad\qquad\qquad\, \displaystyle {\color{Red} {\lim_{x \to \infty}}}\,{10 \over x\,-\,2} {\color{Red} { \; = \; 0}} \)

Grafiskt:  Kurvan närmar sig \( \, x \)-axeln när \( \, x \, \) växer, dvs \( \, y\, \) blir allt mindre ju större \( \, x \, \) blir.

Men kurvan skär aldrig \( \, x \)-axeln. Funktionen går mot \( \, 0\, \) utan att nå \( \, 0 \).

Analytiskt:  Ekvationen \( \, \displaystyle {10 \over x\,-\,2} \, = \, 0 \, \) saknar lösning, därför att täljaren \( \, 10\, \) är en konstant som aldrig kan bli \( \, 0 \). Så kan inte heller \( \, \displaystyle {10 \over x\,-\,2} \, \) bli \( \, 0 \, \), oavsett \( \, x \). Nämnaren växer däremot obegränsat när \( \, x \, \) växer. Konstant delad med obegränsat växande värden går mot \( \, 0 \, \). Man skriver:

\( \displaystyle {10 \over x\,-\,2} \to 0 \quad {\rm när} \quad x \to \infty \;\; \), bättre uttryckt: \( \, \boxed{ \displaystyle \lim_{x \to \infty}\,{10 \over x\,-\,2} \, = \, 0} \, \). Av samma anledning är: \( \, \boxed{ \displaystyle \lim_{x \to \infty}\,{1 \over x} \, = \, 0} \, \).

Vad händer med \( \, y \, \) när \( \; x \to - \infty \; \)?

Något liknande visas när \( \, x \, \) går mot negativa värden, dvs när \( x \to \, {\color{Red} {- \infty}} \):   \( \,y\, \) mot \( \,0\, \) bara att \( \, y\, \) nu närmar sig \( \, 0 \, \) nedifrån, kort: \( \;\; y \to 0 \quad {\rm när} \quad x \to {\color{Red} {- \infty}} \; \).

"Paradoxen" att funktionen allt mer närmar sig \( \, 0 \, \) utan att någonsin bli \( \, 0 \), löses upp och kan därmed hanteras analytiskt med hjälp av limes som generellt beskriver fenomenet att närma sig ett värde allt mer utan att nå det någonsin.


Existens av gränsvärden

I exemplet ovan bestämdes \( \, \displaystyle \lim_{x \to \infty}\,{10 \over x\,-\,2} \, \) utan att fråga om gränsvärdet överhuvudtaget existerade. Att gränsvärdet sedan blev \( \, 0 \, \) bevisade ju existensen. Men det finns faktiskt fall där ett gränsvärde inte existerar och därför inte heller kan bestämmas. Det vore bra om man kunde undersöka det innan man började räkna.

Som exempel tar vi samma funktion som ovan, men betraktar dess beteende för \( \; \color{Red} {x \to 2} \; \).

Exempel på att gränsvärde saknas

Funktionen \( y = f(x) = \displaystyle {10 \over x\,-\,2} \) är given: \( \qquad\qquad\qquad \) Vad händer med \( \, y \, \) när \( \; x \to 2 \; \)?

Bestäm \( \quad \displaystyle \lim_{\color{Red} {x \to 2}}\,{10 \over x\,-\,2} \)

Svar: \( \quad\;\; f(x)\, \) är inte definierad för \( x = 2\, \).

\( \qquad\qquad\qquad\qquad\quad \Downarrow \)

\( \displaystyle \lim_{\color{Red} {x \to 2}}\,{10 \over x\,-\,2} \quad \) existerar inte   :


\( \qquad \) Gränsvärde saknas.

\( \qquad \) Ex 2 Gransvarde.jpg

Grafen visar att kurvan skjuter upp i höjden å ena sidan och ner i "djupet" å andra sidan av punkten \( \, x = 2 \).

Algebraiskt är \( \, f(x)\, \) inte definierad för \( x = 2\, \), för \( \displaystyle{10 \over x\,-\,2} \):s nämnare blir \( \, 0\, \) för \( \, x = 2 \).

Dessutom finns det två olika resultat beroende på om \( \, x \) går mot \( \, 2 \) från höger eller från vänster:

\( f(x)\, \) går mot \( +\, \infty \) när man närmar sig \( \, x = 2 \) från höger och mot \( -\, \infty \) när man närmar sig \( \, x = 2 \) från vänster.

\( y \;\; {\rm går\;mot} \, +\infty \; {\rm när} \; x \; {\rm går\;mot} \, 2 \;{\rm från\;höger:} \; \qquad\quad y \to +\infty \quad {\rm när} \quad x \to 2^+ \)

\( y \;\; {\rm går\;mot} \, -\infty \; {\rm när} \; x \; {\rm går\;mot} \, 2 \;{\rm från\;vänster:} \; \qquad\; y \to -\infty \quad {\rm när} \quad x \to 2^- \)

där \( x \to 2^+ \) betyder att närma sig \( \, x = 2 \) från höger (\( \, x > 2 \)) och \( x \to 2^- \) att närma sig \( \, x = 2 \) från vänster (\( \, x < 2 \)).


Följande modifierad variant av Exempel 2 (\( \, {\color{Red} {x \to 0}} \, \) istället för \( \, x \to \infty \)) är ytterligare ett exempel på att gränsvärdet saknas:


Exempel 2 a

Bestäm \( \qquad \displaystyle \lim_{x \to 0}\, {4\,x\,+\,5 \over x} \)

Lösning:

\[ \lim_{x \to 0^+}\, {4\,x\,+\,5 \over x} \, = \, \lim_{x \to 0^+}\, \left(4 \,+\, {5 \over x}\right) \,= \, +\infty \]
\[ \lim_{x \to 0^-}\, {4\,x\,+\,5 \over x} \, = \, \lim_{x \to 0^-}\, \left(4 \,+\, {5 \over x}\right) \,= \, -\infty \]

där \( x \to 0^+ \) betyder att närma sig \( \, x = 0 \) från höger (\( \, x > 0 \)) och \( x \to 0^- \) att närma sig \( \, x = 0 \) från vänster (\( \, x < 0 \)).

Anmärkning: Sättet att skriva limes som ovan förklaras nedan i Ensidiga och oegentliga gränsvärden.

Svar: \( \qquad\;\; \) Gränsvärde saknas.


Men även om en funktion skulle gå mot t.ex. mot \( +\,\infty \), för ett visst \( \, x \) både från höger och vänster, t.ex. \( \displaystyle {f(x) = {1 \over x^2}} \) för \( \, x = 0 \), skulle det strikt matematiskt inte vara korrekt att säga att limes existerar och är \( +\,\infty \), därför att \( \infty \) inte är något värde. Med andra ord:


Ett gränsvärde måste, för att existera, vara både entydigt och ändligt.


Därför är det matematiskt korrekt att säga: Gränsvärdena \( \; \displaystyle {\lim_{x \to 2}\,{10 \over x - 2}} \; \) och \( \; \displaystyle {\lim_{x \to 0}\,{1 \over x^2}} \;\) existerar inte.


Ensidiga och oegentliga gränsvärden

Skiljer man närmandet från höger till \( \, x = 2 \, \) från närmandet från vänster kan man bilda s.k. ensidiga gränsvärden:

\[ \lim_{x \to 2^{+}}\,{10 \over x - 2}\,=\,+\,\infty \qquad\quad \; {\rm och} \; \qquad\quad \lim_{x \to 2^{-}}\,{10 \over x - 2}\,=\,-\,\infty \]

där \( x \to 2^+ \) betyder att närma sig \( \, x = 2 \) från höger (\( \, x > 2 \)) och \( x \to 2^- \) att närma sig \( \, x = 2 \) från vänster (\( \, x < 2 \)).

Man pratar om höger- och vänstergränsvärdet genom att skilja mellan de två sätten att närma sig talet \( \, 2 \) på \( \, x\)-axeln: från höger \( x \to 2^+ \) och från vänster \( x \to 2^- \), därav beteckningen ensidig. I vårt exempel ger de också två olika resultat.

Gränsvärden av funktioner som går mot oändligheten (och därmed strikt talat inte existerar), men ändå skrivs med limessymbolen, kallar man oegentliga gränsvärden.

Exempel

\( \qquad\qquad\qquad\qquad\qquad \displaystyle {\lim_{x \to 0}\,{1 \over x^2}}\,=\,+\,\infty \)


Grafen visar att funktionen \( \displaystyle f(x) = {1 \over x^2} \) går mot \( +\,\infty \) både

när \( \, x \to 0 \) från höger (\( \, x > 0 \)) och från vänster (\( \, x < 0 \)). Visserligen

är gränsvärdet entydigt, men det är oändligt och kallas därför oegentligt.


Däremot är \( \displaystyle \lim_{x \to 2}\,{10 \over x - 2} \) varken entydigt eller ändligt. Därför existerar det inte.

\( \qquad \) Y = 1 genom x^2.jpg

Att man använder det ovannämnda skrivsättet för ensidiga och oegentliga gränsvärden sker av praktiska skäl. Man ersätter pilarna som vi använde inledningsvis med att beskriva gränsprocessen med limessymbolen istället. Det är bekvämt att använda en enhetlig notation för att beskriva gränsprocesser. Är man medveten om att limes enligt den strikta definitionen inte existerar, är det o.k.

OBS! Av skrivsättet för ensidiga och oegentliga gränsvärden följer fortfarande inte att \( \; \displaystyle {\lim_{x \to 2}\,{10 \over x - 2}} \; \) eller \( \; \displaystyle {\lim_{x \to 0}\,{1 \over x^2}} \; \) existerar.



Internetlänkar

https://www.youtube.com/watch?v=_oPD-c8IAzs

https://www.youtube.com/watch?v=StP64lMXZjA

https://www.youtube.com/watch?v=fPOX0QX8AH0






Copyright © 2020 TechPages AB. All Rights Reserved.

Hämtad från "https://matte3c.mathonline.se/index.php?title=2.3_Fördjupning_till_Gränsvärde&oldid=36739"