Skillnad mellan versioner av "3.3 Terasspunkter"

Från Mathonline
Hoppa till: navigering, sök
m (→‎Lurig graf)
m
Rad 17: Rad 17:
  
 
== Terasspunkter ==
 
== Terasspunkter ==
 +
 +
== Exempel 1 Vinternattens kallaste tidpunkt ==
 +
 +
Vi återgår till [[3.1_Växande_och_avtagande#Exempel_1_Vinternatt|<strong><span style="color:blue">Exempel 1</span></strong>]] i förra avsnitt, men byter frågeställning: Vi tittar inte längre på funktionens växande eller avtagande utan på funktionens minsta värde (minimum):
 +
 +
Under en vinternatt varierar temperaturen enligt funktionen <math> {\color{White} x} \; y \, = \, f(x) \, = \, 0,24\,x^2\,-\,2,4\,x\,+\,7 {\color{White} x} \; </math> med definitionsområdet<span style="color:black">:</span> <math> \quad 0 \leq x \leq 8 </math>.
 +
 +
där &nbsp;&nbsp; <math> y \; = </math> &nbsp; temperaturen i grader Celsius och
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; <math> x \; = </math> &nbsp; tiden i timmar efter midnatt
 +
 +
a) &nbsp; Ställ upp första- och andraderivatan. Rita graferna till <math> \,f(x) </math>, <math> \,f'(x) </math> och <math> \,f''(x) </math> i separata koordinatsystem.
 +
 +
b) &nbsp; Bestäm nattens kallaste tidpunkt algebraiskt.
 +
 +
c) &nbsp; Bestäm nattens lägsta temperatur algebraiskt.
 +
----
 +
 +
 +
'''Lösning:'''
 +
 +
a) &nbsp; <math> f(x) \, = \, 0,24\,x^2 - 2,4\,x + 7 </math>
 +
 +
::<math> f'(x) \, = \, 0,48\,x - 2,4 </math>
 +
 +
::<math> f''(x) \, = \, 0,48 </math>
 +
 +
[[Image: Ex 1 Vinternatt Funktionen.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Ex 1 Vinternatt Derivatana.jpg]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Image: Ex 1 Vinternatt Andraderivatan.jpg]]
 +
----
 +
 +
 +
b) &nbsp; För att få reda på derivatans nollställe som [[3.2_Maxima_och_minima#Regler_om_maxima_och_minima_med_andraderivata|<strong><span style="color:blue">reglerna om maxima och minima med andraderivata</span></strong>]] kräver sätter vi derivatan till <math> \, 0 </math> och beräknar den tidpunkt <math> x \, </math> då derivatan blir <math> \, 0 </math>:
 +
 +
::<math>\begin{array}{rcrcl}  f'(x) & = & 0,48\,x - 2,4 & = & 0  \\
 +
                                    &  & 0,48\,x      & = & 2,4 \\
 +
                                    &  &      x      & = & {2,4 \over 0,48} \\
 +
                                    &  &      x      & = & 5
 +
  \end{array}</math>
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Nu vet vi att derivatan blir <math> \, 0 </math> i <math> x = 5 \, </math> dvs tangenten till kurvan <math> y = f(x) \, </math> har lutningen <math> 0\, </math> dvs är horisontell i <math> x = 5 \, </math>.
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Därmed är det bevisat att <math> \, x = 5 \, </math> är en extrempunkt. Men en extrempunkt kan vara ett maximum eller ett minimum.
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; För att avgöra om denna extrempunkt är ett maximum eller ett minimum kräver regeln andraderivatans tecken.
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Därför sätter vi <math> x = 5 \, </math> in i andraderivatan och kollar om den blir positiv eller negativ:
 +
 +
:::::<math> f''(5) = 0,48 \,>\, 0 </math>
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Andraderivatan är positiv (konstant) för alla <math> x \, </math> och därmed även för <math> x = 5 \, </math>. Därav följer att <math> f(x) \, </math> har ett minimum i <math> x_{min} = 5 \, </math>.
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Alltså är nattens kallaste tidpunkt kl <math> 5 \, </math>.
 +
----
 +
 +
 +
c) &nbsp; Temperaturen vid kl <math> 5 \, </math> är:
 +
 +
::<math> f(x_{min}) = f(5) = 0,24 \cdot 5^2 - 2,4 \cdot 5 + 7  = 1 </math>
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Alltså är nattens lägsta temperatur <math> 1 \, </math> grad Celsius.
 +
 +
+++
 +
Två kriterier behövs för att få reda på en funktions maxima och minima: ett om derivatans nollställen, ett om andraderivatans tecken. Båda måste vara uppfyllda. Följande regler gäller:
 +
 +
<span style="color:white">:</span>
 +
<div style="border:1px solid black;display:inline-table;margin-left: 15px;padding:10px 20px 10px 20px;-webkit-border-radius: 15px;">
 +
<big>'''Derivatans nollställen och andraderivatans tecken avgör för vilka <math>\, x </math> en funktion har maxima resp. minima''':
 +
 +
 +
Funktionen <math> {\color{White} x} y \, = \, f(x) {\color{White} x} </math> har ett <strong><span style="color:red">maximum</span></strong> i <math> {\color{White} x} x = a {\color{White} x}  </math> om derivatan <math> {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} </math> och andraderivatan <math> {\color{White} x} f\,''(a) \, {\bf {\color{Red} <}} \, 0 {\color{White} x}. </math>
 +
----
 +
Funktionen <math> {\color{White} x} y \, = \, f(x) {\color{White} x} </math> har ett <strong><span style="color:red">minimum</span></strong> i <math> {\color{White} x} x = a {\color{White} x}  </math> om derivatan <math> {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} </math> och andraderivatan <math> {\color{White} x} f\,''(a) \, {\bf {\color{Red} >}} \, 0 {\color{White} x}. </math>
 +
----
 +
Om derivatan <math> {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} </math> och andraderivatan <math> {\color{White} x} f\,''(a) \, {\bf {\color{Red} =}} \, 0 {\color{White} x} </math> har funktionen varken ett maximum eller ett minimum.
 +
</big></div>
 +
 +
 +
<table>
 +
<tr>
 +
  <td>Reglerna ovan säger i ord:
 +
 +
 +
 +
 +
 +
  </td>
 +
  <td>Där derivatan är <math> \, 0 </math> och andraderivatan är negativ har funktionen ett maximum.
 +
 +
Där derivatan är <math> \, 0 </math> och andraderivatan är positiv har funktionen ett minimum.
 +
 +
Där både derivatan och andraderivatan är <math> \, 0 </math> föreligger varken ett maximum eller ett minimum. Vad som gäller då behandlas i [[3.3 Kurvkonstruktion med derivata|<strong><span style="color:blue">nästa avsnitt</span></strong>]].
 +
</td>
 +
</tr>
 +
</table>
  
  

Versionen från 27 december 2014 kl. 22.45

       <-- Förra avsnitt          Teori          Övningar          --> Nästa avsnitt      


Lektion 31 Kurvkonstruktion med derivata I

Lektion 32 Kurvkonstruktion med derivata II


Terasspunkter

Exempel 1 Vinternattens kallaste tidpunkt

Vi återgår till Exempel 1 i förra avsnitt, men byter frågeställning: Vi tittar inte längre på funktionens växande eller avtagande utan på funktionens minsta värde (minimum):

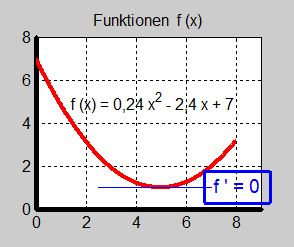
Under en vinternatt varierar temperaturen enligt funktionen \( {\color{White} x} \; y \, = \, f(x) \, = \, 0,24\,x^2\,-\,2,4\,x\,+\,7 {\color{White} x} \; \) med definitionsområdet: \( \quad 0 \leq x \leq 8 \).

där    \( y \; = \)   temperaturen i grader Celsius och

         \( x \; = \)   tiden i timmar efter midnatt

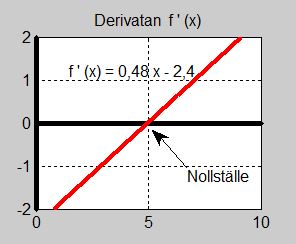
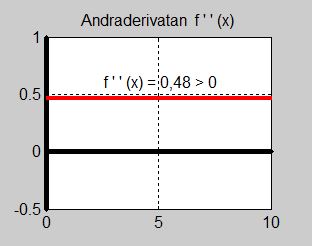
a)   Ställ upp första- och andraderivatan. Rita graferna till \( \,f(x) \), \( \,f'(x) \) och \( \,f''(x) \) i separata koordinatsystem.

b)   Bestäm nattens kallaste tidpunkt algebraiskt.

c)   Bestäm nattens lägsta temperatur algebraiskt.


Lösning:

a)   \( f(x) \, = \, 0,24\,x^2 - 2,4\,x + 7 \)

\[ f'(x) \, = \, 0,48\,x - 2,4 \]
\[ f''(x) \, = \, 0,48 \]

Ex 1 Vinternatt Funktionen.jpg      Ex 1 Vinternatt Derivatana.jpg      Ex 1 Vinternatt Andraderivatan.jpg


b)   För att få reda på derivatans nollställe som reglerna om maxima och minima med andraderivata kräver sätter vi derivatan till \( \, 0 \) och beräknar den tidpunkt \( x \, \) då derivatan blir \( \, 0 \):

\[\begin{array}{rcrcl} f'(x) & = & 0,48\,x - 2,4 & = & 0 \\ & & 0,48\,x & = & 2,4 \\ & & x & = & {2,4 \over 0,48} \\ & & x & = & 5 \end{array}\]

      Nu vet vi att derivatan blir \( \, 0 \) i \( x = 5 \, \) dvs tangenten till kurvan \( y = f(x) \, \) har lutningen \( 0\, \) dvs är horisontell i \( x = 5 \, \).

      Därmed är det bevisat att \( \, x = 5 \, \) är en extrempunkt. Men en extrempunkt kan vara ett maximum eller ett minimum.

      För att avgöra om denna extrempunkt är ett maximum eller ett minimum kräver regeln andraderivatans tecken.

      Därför sätter vi \( x = 5 \, \) in i andraderivatan och kollar om den blir positiv eller negativ:

\[ f''(5) = 0,48 \,>\, 0 \]

      Andraderivatan är positiv (konstant) för alla \( x \, \) och därmed även för \( x = 5 \, \). Därav följer att \( f(x) \, \) har ett minimum i \( x_{min} = 5 \, \).

      Alltså är nattens kallaste tidpunkt kl \( 5 \, \).


c)   Temperaturen vid kl \( 5 \, \) är:

\[ f(x_{min}) = f(5) = 0,24 \cdot 5^2 - 2,4 \cdot 5 + 7 = 1 \]

      Alltså är nattens lägsta temperatur \( 1 \, \) grad Celsius.

+++ Två kriterier behövs för att få reda på en funktions maxima och minima: ett om derivatans nollställen, ett om andraderivatans tecken. Båda måste vara uppfyllda. Följande regler gäller:

:

Derivatans nollställen och andraderivatans tecken avgör för vilka \(\, x \) en funktion har maxima resp. minima:


Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett maximum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och andraderivatan \( {\color{White} x} f\,''(a) \, {\bf {\color{Red} <}} \, 0 {\color{White} x}. \)

Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett minimum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och andraderivatan \( {\color{White} x} f\,''(a) \, {\bf {\color{Red} >}} \, 0 {\color{White} x}. \)

Om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och andraderivatan \( {\color{White} x} f\,''(a) \, {\bf {\color{Red} =}} \, 0 {\color{White} x} \) har funktionen varken ett maximum eller ett minimum.


Reglerna ovan säger i ord:



Där derivatan är \( \, 0 \) och andraderivatan är negativ har funktionen ett maximum.

Där derivatan är \( \, 0 \) och andraderivatan är positiv har funktionen ett minimum.

Där både derivatan och andraderivatan är \( \, 0 \) föreligger varken ett maximum eller ett minimum. Vad som gäller då behandlas i nästa avsnitt.


Ingen terasspunkt

Globala maxima och minima

Exempel på kurvkonstruktion

Ett lurigt fall

Hämtad från "https://matte3c.mathonline.se/index.php?title=3.3_Terasspunkter&oldid=19504"