Skillnad mellan versioner av "3.4 Kurvkonstruktioner"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m (→Globalt extremum saknas) |
||
| Rad 66: | Rad 66: | ||
== Globalt extremum saknas == | == Globalt extremum saknas == | ||
| − | En problematik som kan dyka upp när man är ute efter globala extrema är att de inte existerar. | + | En problematik som kan dyka upp när man är ute efter globala extrema är att de inte existerar, vilket inte nödvändigtvis har att göra med funktionens egenskaper utan snarare med funktionens definitionsintervall. Därför tittar vi på två olika typer av intervall: |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
== Exempel på en kurvkonstruktion == | == Exempel på en kurvkonstruktion == | ||
Versionen från 15 januari 2015 kl. 14.45
| <-- Förra avsnitt | Teori | Övningar | --> Nästa avsnitt |
Innehåll
Fortfarande förutsätts att alla funktioner \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) vi behandlar här är kontinuerliga i alla punkter av det betraktade området.
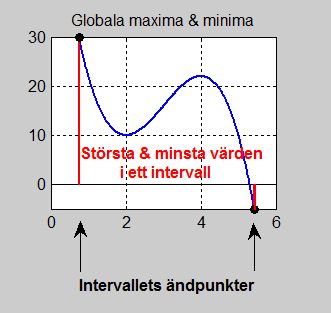
Globala maxima och minima
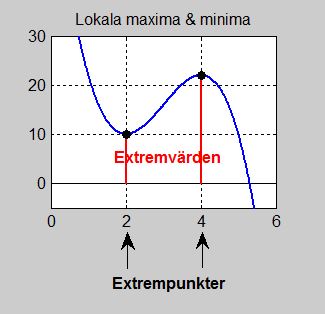
I avsnittet om Lokala maxima och minima hade vi tittat på sådana punkter som hade maximala och minimala \( \, y\)-värden i sin närmaste omgivning, därför "lokala", se bilden till höger.
I detta avsnitt ska vi betrakta sådana punkter som har största och minsta \( \, y\)-värden i ett intervall, därför "globala", se bilden till vänster.
 |
Globala maxima och minima är en funktions största och minsta värden
globalt dvs i ett intervall, närmare bestämt: Med globala maxima och globala minima menas punkter som har största resp. minsta \( \, y\)-värden i funktionens hela definitionsområde. På bilden till vänster visas de med • . Funktionens största värde är \( \, 30 \, \) och dess minsta värde är \( \, -5 \, \) (OBS! \( \, y\)-värden).
minima eller i intervallets ändpunkter.
annars än att de ev. är identiska med funktionens lokala extrema. I ett mindre intervall blir exemplets lokala extrema, även globala. |
 |
I praktiken hittar man en funktions globala extrema genom att:
- Hitta funktionens lokala extrema med någon av de regler vi lärde oss i förra avsnitt (andraderivatan eller teckenstudium).
- Beräkna de lokala extremvärdena.
- Beräkna funktionsvärdena i definitionsintervallets ändpunkter.
- Jämföra de lokala extremvärdena med värdena i definitionsintervallets ändpunkter.
Globalt extremum saknas
En problematik som kan dyka upp när man är ute efter globala extrema är att de inte existerar, vilket inte nödvändigtvis har att göra med funktionens egenskaper utan snarare med funktionens definitionsintervall. Därför tittar vi på två olika typer av intervall:
