Skillnad mellan versioner av "3.4 Kurvkonstruktioner"

Versionen från 16 januari 2015 kl. 16.00

Lektion 32 Kurvkonstruktioner

Fortfarande förutsätts att alla funktioner \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) vi behandlar här är kontinuerliga i alla punkter av det betraktade området.

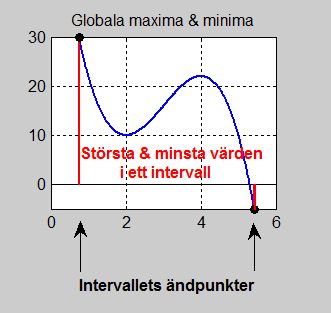
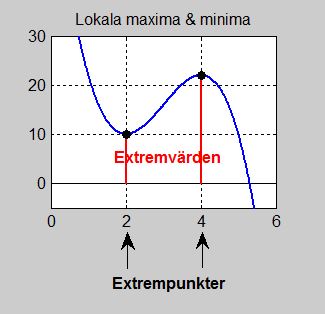
Globala maxima och minima

I avsnittet om Lokala maxima och minima hade vi tittat på sådana punkter som hade maximala och minimala \( \, y\)-värden i sin närmaste omgivning, därför "lokala", se bilden till höger.

I detta avsnitt ska vi betrakta sådana punkter som har största och minsta \( \, y\)-värden i ett intervall, därför "globala", se bilden till vänster.

Globala maxima och minima är en funktions största och minsta värden      globalt dvs i ett intervall, närmare bestämt:      Med globala maxima och globala minima menas punkter som har      största resp. minsta \( \, y\)-värden i funktionens hela definitionsområde.      På bilden till vänster visas de med   •  . Funktionens största värde är \( \, 30 \, \)      och dess minsta värde är \( \, -5 \, \) (OBS! \( \, y\)-värden).      Globala maxima och minima antas antingen i de lokala maxima och      minima eller i intervallets ändpunkter.      Globala maxima och minima identifieras i regel inte med derivatan,      annars än att de ev. är identiska med funktionens lokala extrema.      I ett mindre intervall blir exemplets lokala extrema, även globala.

I praktiken hittar man en funktions globala extrema genom att:

1. Hitta funktionens lokala extrema med någon av de regler vi lärde oss i förra avsnitt (andraderivatan eller teckenstudium).
2. Beräkna de lokala extremvärdena.
3. Beräkna funktionsvärdena i definitionsintervallets ändpunkter.
4. Jämföra de lokala extremvärdena med värdena i definitionsintervallets ändpunkter.

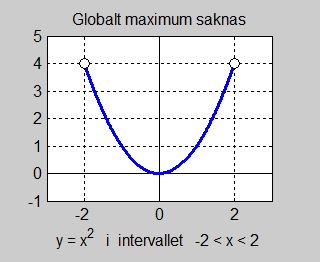
Globalt extremum saknas

En funktion behöver inte nödvändigtvis ha extrema, varken lokala eller globala.

Detta kan hända \(-\) som det följande exemplet visar \(-\) när man letar efter globala extrema där man förväntar dem, t.ex. i definitionsintervallets ändpunkter.

Exempel:

Följande funktion är definierad i det angivna intervallet:

\( y \, = \, f(x) \, = \, x^2 \quad \) Definitionsmängden: \( \quad -2 < x < 2 \)

Av någon anledning är intervallets ändpunkter inte inkluderade i definitionsmängden. Dvs \( f(x) \) är inte definierad för \( \, x = 2 \), inte heller för \( \, x = -2 \). Grafen till höger visar detta genom de ihåliga ringarna i kurvans ändpunkter. \( f(x) \) har i \( x = 0 \) ett lokalt minimum som är även funktionens globala minimum. Däremot kan man inte ange något globalt maximum för \( f(x) \), av följande skäl: Om man t.ex. påstår att \( f(1,99) \) är funktionens största värde, är \( f(1,999) \) ännu större. Om man påstår att \( f(1,999) \) är största värdet, är \( f(1,9999) \) ännu större osv. Denna process har ingen ända och gäller även för \( f(-1,99\ldots) \). Varken \( f(2) \) eller \( f(-2) \) kan vara globala maxima, för båda är inte definierade. Slutligen kan man inte hitta något största värde: Globalt maximum saknas.

Att globalt maximum saknas har inte med funktionens egenskaper att göra utan snarare med intervallets där \( f(x) \) är definierad.

Man säger att definitionsintervallet \( \; -2 < x < 2 \; \) är "öppet": Ändarna tillhör inte intervallet.

Hade \( f(x) \) däremot varit definierad t.ex. i det "slutna" intervallet: \( -2 \leq x \leq 2 \;\; \) hade \( \; f(2) \, = \, f(-2) \, = \, 4 \; \) varit funktionens globala maximum.

I praktiken behöver man inte leta efter globala extrema i definitionsintervallets ändpunkter om funktionen är definierad i ett öppet intervall.

Ett enkelt exempel på kurvkonstruktion

Funktionen:

     \( f(x) \, = \, x^3 \, - \, 12\,x^2 \, + \, 45\,x \, - \, 44 \qquad \) är definierad i intervallet \( \qquad 1 \leq x \leq 7 \)

a)   Undersök algebraiskt om \( \,f(x) \, \) har några lokala maximi-, minimi- eller terasspunkter. Om ja, ange deras koordinater.

b)   Bestäm funktionens största och minsta värden i definitionsintervallet.

c)   Skissa grafen till \( \, f(x) \, \) utgående från information från a) och b).

a)  

Steg 1   Derivera två gånger:

\[\begin{array}{rcl} f(x) & = & x^3 - 12\,x^2 + 45\,x - 44 \\ f'(x) & = & 3\,x^2 - 24\,x + 45 \\ f''(x) & = & 6\,x - 24 \end{array}\]

Steg 2   Sätt derivatan till \( \, 0 \):

\[\begin{array}{rcl} 3\,x^2 - 24\,x + 45 & = & 0 \end{array}\]

Steg 3   Lös ekvationen som uppstår:

\[\begin{array}{rcl} 3\,x^2 - 24\,x + 45 & = & 0 \\ x^2 - 8\,x + 15 & = & 0 \\ \end{array}\]

\[ \begin{array}{rcl} {\rm Vieta:} \quad x_1 \cdot x_2 & = & 15 \\ x_1 + x_2 & = & -(-8) = 8 \\ &\Downarrow& \\ x_1 & = & 3 \\ x_2 & = & 5 \end{array}\]

Steg 4   Sätt in i andraderivatan:

Nollställe 1 \( {\color{White} x} x_1 = 3 \quad {\color{White} x} \)

\[ f''(x) \, = \, 6\,x - 24 \]

\[ f''(3) \, = \, 6\cdot 3 - 24 = -6 < 0 \]+++

Andraderivatan är positiv för \( t_1 = 2 \, \). Slutsats: \( V(t) \, \) har ett minimum i \( t_1 = 2 \, \).

Nollställe 2: \( {\color{White} x} t_2 = 4 \quad {\color{White} x} \)

Vi sätter in \( t_2 = 4 \, \) in i andraderivatan och kollar om den blir positiv eller negativ:

\[ V''(4) \, = \, -18\cdot 4 + 54 = -18 < 0 \]

Andraderivatan är negativ för \( t_2 = 4 \, \). Slutsats: \( V(t) \, \) har ett maximum i \( t_2 = 4 \, \).

Ett lurigt exempel på kurvkonstruktion