Skillnad mellan versioner av "Kapitel 4 Integraler"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 30: | Rad 30: | ||
</tr> | </tr> | ||
</table> | </table> | ||
| − | |||
| − | |||
| − | |||
<div class="border-divblue"> | <div class="border-divblue"> | ||
| − | Integration är den <strong><span style="color:red">inversa</span></strong> operationen till derivering. | + | Integration är den <strong><span style="color:red">inversa</span></strong> operationen till derivering. <big><b><span style="color:red">Primitiv funktion = "Anti"derivatan</span></b></big> |
---- | ---- | ||
Fysikalisk tolkning<span style="color:black">:</span> <math> \qquad\;\;\, </math> Derivata = Hastighet <math> \qquad\qquad\, </math> Integral = Sträcka | Fysikalisk tolkning<span style="color:black">:</span> <math> \qquad\;\;\, </math> Derivata = Hastighet <math> \qquad\qquad\, </math> Integral = Sträcka | ||
Versionen från 18 februari 2016 kl. 15.27
Utdrag ur planeringen:
4.1 Primitiva funktioner
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 175
| \( \quad \) | 
|
\( \qquad \) |
Integration är den inversa operationen till derivering. Primitiv funktion = "Anti"derivatan
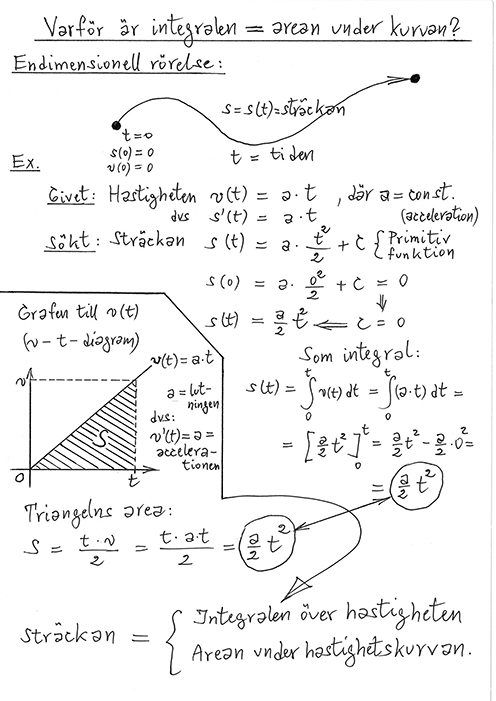
Fysikalisk tolkning: \( \qquad\;\;\, \) Derivata = Hastighet \( \qquad\qquad\, \) Integral = Sträcka
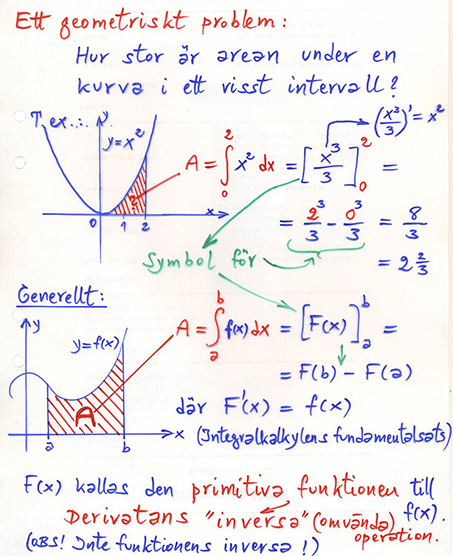
Geometrisk tolkning: \( \qquad \) Derivata = Kurvans lutning \( \qquad \) Integral = Area under kurvan (se 4.3)
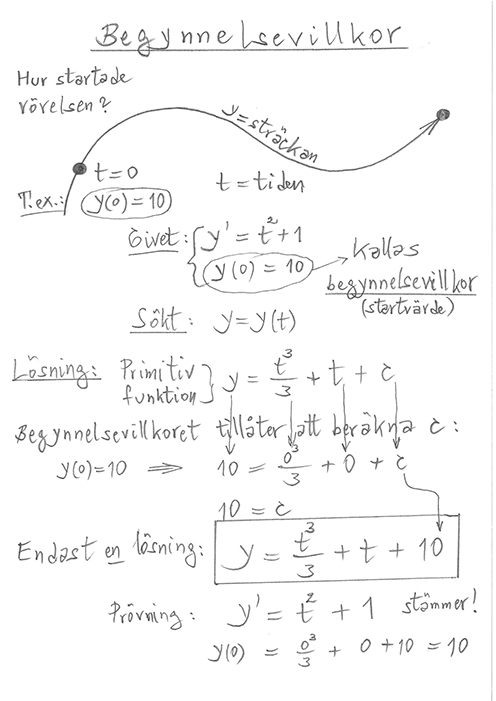
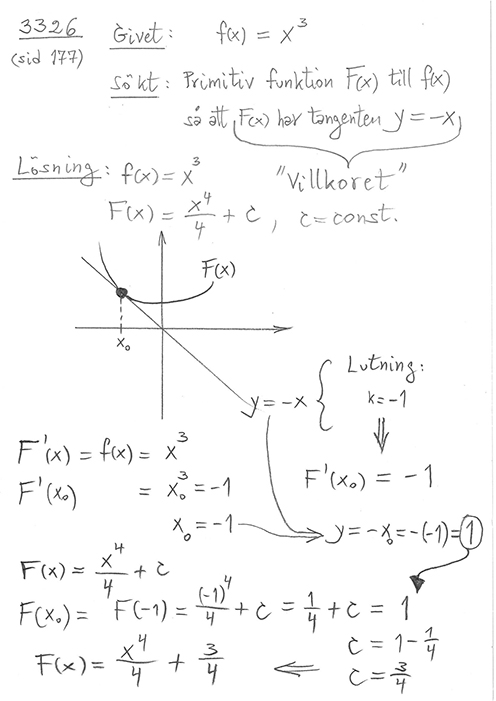
4.2 Primitiva funktioner med villkor
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 177
4.3 Integral som area under kurvan
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 180
4.4 Integralberäkning med primitiv funktion
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 185
4.5 Användning av integraler
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 188-90
Copyright © 2011-2016 Math Online Sweden AB. All Rights Reserved.