Skillnad mellan versioner av "Kapitel 4 Integraler"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 116: | Rad 116: | ||
<div style="border:1px solid black;display:inline-table;margin-left: 50px;"> [[Image: 4 Int_ber_prim_fkt_D174_3434_20.jpg]] </div> | <div style="border:1px solid black;display:inline-table;margin-left: 50px;"> [[Image: 4 Int_ber_prim_fkt_D174_3434_20.jpg]] </div> | ||
| + | |||
| + | |||
| + | När en integral har bestämda integrationsgränser, så som i exemplen a) och b) ovan, finns inga villkor med i uppgiften. Då ar villkoret inbakat i integrationsgränserna. En sådan integral kallas för en ''bestämd integral'' och dess resultat är ett tal. | ||
| + | |||
| + | När en integral inte har några integrationsgränser, är dess resultat inget tal, utan en funktion, närmare bestämt den primitiva funktionen. Då borde även ett villkor vara med för att bestämma en entydig primitiv funktion. Fattas villkoret måste man alltid addera den s.k. integrationskonstant C, vilket gör att resultatet blir oändligt många funktioner. En sådan integral kallas för en ''obestämd integral''. | ||
Versionen från 26 april 2016 kl. 20.42
| <-- Förra kapitel | Start Matte 3c | Planering Matte 3c | Formelsamling Integraler | Nästa kapitel --> |
Utdrag ur planeringen:
4.1 Primitiva funktioner
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 175
| \( \quad \) | 
|
\( \qquad \) |
Integration är den inversa operationen till derivering. \( \quad \) Primitiv funktion = "Anti"derivata
Derivata Integral Fysikalisk tolkning: Hastighet Sträcka Geometrisk tolkning: Kurvans lutning Area under kurvan Matematisk tolkning: Limes av differenskvot Limes av oändlig summa
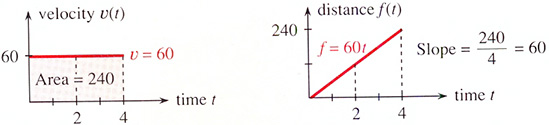
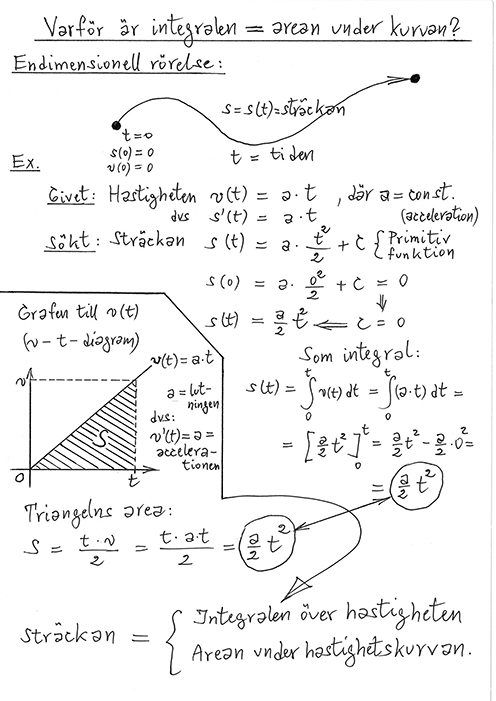
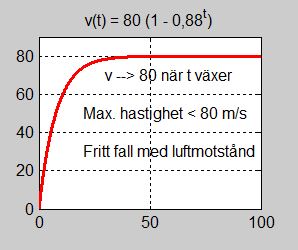
Ex. på "Area under kurvan" : \( \quad \) Rörelse med konstant hastighet 60 km/h
OBS! Area under kurvan är det inversa till kurvans lutning (eng. slope), när det gäller integration vs. derivering.
Sammanfattning: Givet: \( \quad f\,(x) \) Sökt: \( \quad \) Primitiv funktion \( \; F\,(x) \quad \) så att \( \quad F\,'\,(x) = f\,(x) \) |
Ex.: \( f\,(x) \; = \; x\,^3 + 5 \) \( F(x) = \frac{1}{4} x\,^4 + 5 x + C \, , \; C={\rm const.} \) |
\( \;\qquad\; C \; \) kallas för integrationskonstanten och bestäms av villkor (krav) som ställs på \( \, F(x) \, \). \( \quad {\bf {\color{Red} {\downarrow}}} \quad \)
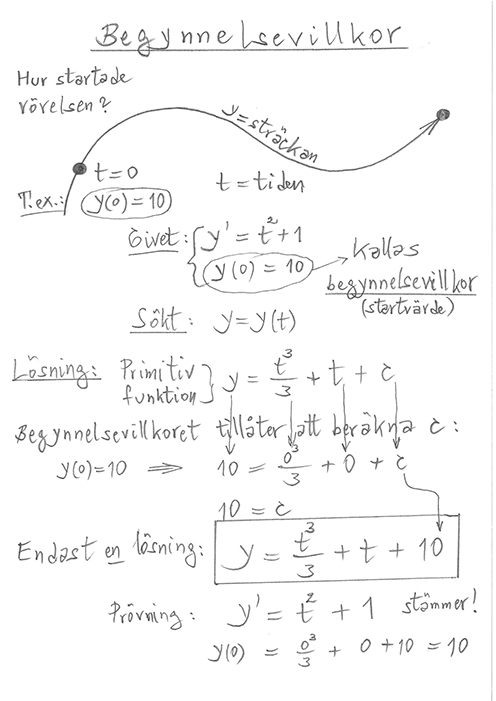
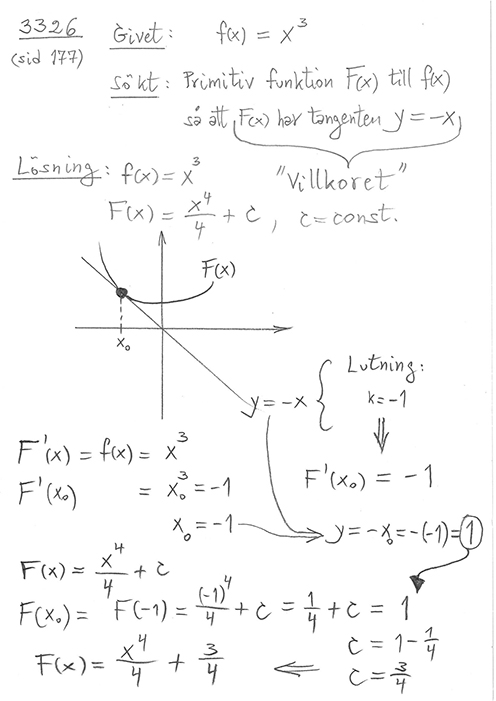
4.2 Primitiva funktioner med villkor
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 177
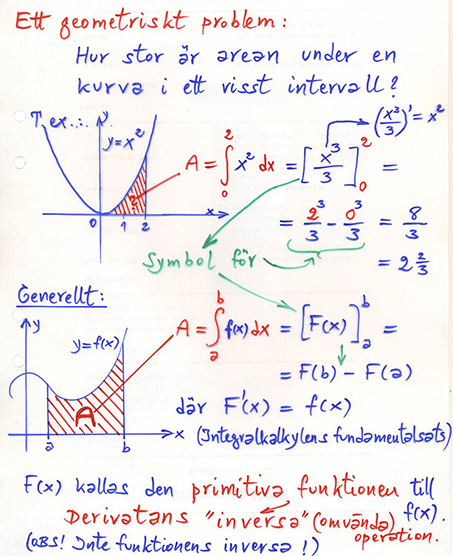
4.3 Integral som area under kurvan
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 180
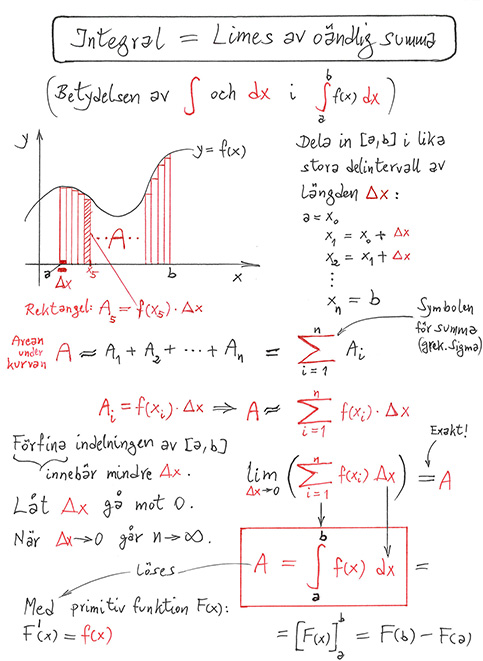
Parentes: Integral som Limes av oändlig summa
4.4 Integralberäkning med primitiv funktion
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 185
När en integral har bestämda integrationsgränser, så som i exemplen a) och b) ovan, finns inga villkor med i uppgiften. Då ar villkoret inbakat i integrationsgränserna. En sådan integral kallas för en bestämd integral och dess resultat är ett tal.
När en integral inte har några integrationsgränser, är dess resultat inget tal, utan en funktion, närmare bestämt den primitiva funktionen. Då borde även ett villkor vara med för att bestämma en entydig primitiv funktion. Fattas villkoret måste man alltid addera den s.k. integrationskonstant C, vilket gör att resultatet blir oändligt många funktioner. En sådan integral kallas för en obestämd integral.
4.5 Användning av integraler
| \( \quad \) | Genomgång: \( \qquad\qquad\qquad \) Övningar: Boken, sid 188-90
3438 (3c-boken, sid 190): En fallskärmshoppare faller fritt utan att öppna fallskärmen. Hastigheten \( \, v \, \) ökar enligt \( \, v(t) = 80\,(1 - 0,88\,^t) \, \) där \( \, t = \, \) tiden i sek. Hur långt har hopparen fallit när \( \, v = 40 \, \) m/s ? Tillägg: \( \quad \) Vilken maximal hastighet kan hopparen inte överskrida? Vilken slutsats kan man dra därav om vilken typ av fritt fall det handlar om? |
\( \qquad \) |  |
Copyright © 2011-2016 Math Online Sweden AB. All Rights Reserved.
