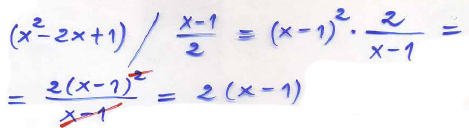Skillnad mellan versioner av "1.3 Rationella uttryck"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 10: | Rad 10: | ||
[[1.2 Faktorisering av polynom|<span style="color:blue"> <math> \pmb{\gets} </math> Förra avsnitt</span>]] | [[1.2 Faktorisering av polynom|<span style="color:blue"> <math> \pmb{\gets} </math> Förra avsnitt</span>]] | ||
| − | [[ | + | [[File: Lektion 6 Rationella uttryck Rutaa.pdf|<b><span style="color:blue">Lektion 6 Rationella uttryck</span></b>]] |
| − | [[ | + | [[File: Lektion 7 Rationella uttryckFb Rutaa.pdf|<b><span style="color:blue">Lektion 7 Rationella uttryck: Fördjupning</span></b>]] |
__NOTOC__ | __NOTOC__ | ||
== <b><span style="color:#931136">Exempel på rationella uttryck</span></b> == | == <b><span style="color:#931136">Exempel på rationella uttryck</span></b> == | ||
Versionen från 16 september 2016 kl. 14.36
| Repetition: Bråkräkning | Genomgång | Övningar | Fördjupning | Nästa avsnitt \( \pmb{\to} \) |
\( \pmb{\gets} \) Förra avsnitt
Lektion 7 Rationella uttryck: Fördjupning
Exempel på rationella uttryck
- \[ {1 \over x} \qquad\qquad {5 \over 2\,x} \qquad\qquad {7\,x \over x+2} \qquad\quad {6\,x \over x^2 - 1} \qquad\quad {x^3 \, + \, 3\,x^2 \, - \, 8\,x - \, 1 \over 4\,x^2 \, - \, 5\,x \, + \, 1} \quad \]
Ett rationellt uttryck är kvoten (resultatet av division) mellan två polynom.
I rationella uttryck får nämnaren inte bli \( \, 0\, \), t.ex. får i:
- \[ 6\,x \over x^2 - 1 \]
nämnaren \( x^2 - 1\, \) inte bli \( \, 0 \), för division med \( \, 0 \) är inte definierad. Läs: Varför är division med 0 inte definierad?
Detta innebär att \( \, x\, \) varken får vara \( \, 1\, \) eller \( \, -1\, \), för då blir polynomet \( \, x^2 - 1\, \):s värde \( \, 0 \). Och eftersom \( \, x^2 - 1\, \) står i nämnaren, blir hela uttryckets värde för \( \, x = 1 \, \) och \( \, x = -1 \, \) inte definierat. Man säger:
Det rationella uttrycket \( \, \displaystyle \frac{6\,x}{x^2 - 1} \, \) är definierat för alla \( x\, \) utom för \( \, x = 1 \, \) och \( \, x = -1 \).
Uttryckets definitionsmängd är: \( \qquad {\rm Alla}\quad x \quad {\rm med} \quad x \neq 1 \quad {\rm och} \quad x \neq -1 \)
Ett uttrycks definitionsmängd är mängden av alla \( \, x \, \) för vilka uttrycket är definierat, jfr. med en funktions definitionsmängd.
Analogi mellan heltal och polynom samt mellan bråk och rationella uttryck
Repetera Olika typer av tal från Matte 1.
Ett rationellt tal är ett tal i bråkform, dvs kvoten (resultatet av division) mellan två heltal med undantaget \( 0\, \) i nämnaren, t.ex. \( \; \displaystyle \frac{3}{4} \; \).
Noll får inte förekomma i nämnaren, för division med \( \, 0\, \), t.ex. \( \, \displaystyle \frac{3}{0} \, \) är inte definierad.
Följande analogi (motsvarighet) råder mellan heltal och polynom å ena och bråk och rationellt uttryck å andra sidan:
Heltal motsvarar polynom och rationella tal motsvarar rationella uttryck. De senaste två är kvoter av de första två. I de senaste två får nämnaren inte bli \( \, 0 \).
De senaste två är utvidgningar av de första två som har kommit till genom division. Inte nog med det:
När vi börjar räkna visar det sig att räknereglerna för rationella uttryck är en naturlig fortsättning på de regler som gäller för bråktal, fast på ett högre plan. Detta gäller inte bara de fyra räknesätten utan även förkortning och förlängning.
I själva verket är räknereglerna för rationella uttryck generaliseringar av bråkräkningens regler. Samma principer som gäller för bråkräkning, kan användas för räkning med rationella uttryck. Därför: Repetera bråkräkning från Matte 1 .
Att räkna med rationella uttryck: Addition & subtraktion
Exempel 1
Förenkla uttrycket \( \; \displaystyle \frac{5}{2\,x} \, - \, \frac{4}{3\,x} \; \) så långt som möjligt.
- \[ \;\, {5 \over 2\,x} \, - \, {4 \over 3\,x} \; = \; {\;5 \;\,\cdot {\color{Red} {3\,x}} \over 2\,x \cdot {\color{Red} {3\,x}}} \, - \, {\;4 \;\,\cdot {\color{Red} {2\,x}} \over 3\,x \cdot {\color{Red} {2\,x}}} \; = \; {\;15\,x \over 6\,x^2} \, - \, {\;8\,x \over 6\,x^2} \; = \; {\;15\,x - 8\,x \over 6\,x^2} \; = \; {7\,x \over 6\,x^2} \; = \; {7 \over 6\,x} \]
Exempel 2
Förenkla uttrycket \( \; \displaystyle \frac{7}{12\,x} \, - \, \frac{3}{8\,x^2} \, + \, \frac{7}{24\,x^3} \; \) så långt som möjligt.
- \[ \;\, {7 \over 12\,x} \, - \, {3 \over 8\,x^2} \, + \, {7 \over 24\,x^3} \; = \; {\;\;7 \;\;\,\cdot {\color{Red} {2\,x^2}} \over 12\,x \cdot {\color{Red} {2\,x^2}}} \, - \, {\;\,3 \;\;\,\cdot {\color{Red} {3\,x}} \over 8\,x^2 \cdot {\color{Red} {3\,x}}} \, + \, {7 \over 24\,x^3} \; = \; \]
- \[ \;\, = \; {14\,x^2 \over 24\,x^3} \, - \, {9\,x \over 24\,x^3} \, + \, {7 \over 24\,x^3} \; = \; {14\,x^2 - 9\,x + 7 \over 24\,x^3} \]
Hjälpsats
- \[ a\,-\,b \; = \; -\,(b\,-\,a) \]
Bevis: \( \qquad\qquad a\,-\,b \; = \; a\,+\,(-\,b) \; = \; (-\,b)\,+\,a \; = \; -\,b\,+\,a \; = \; -\,(b\,-\,a) \)
Dvs: Kastar man om ordningen i en subtraktion, måste minus sättas framför det hela.
Exempel 3
Förenkla uttrycket \( \; \displaystyle \frac{2}{a-b} \, - \, \frac{1}{b-a} \; \) så långt som möjligt.
- \[ \;\, {2 \over a-b} \, - \, {1 \over b-a} \; = \; {2 \over a-b} \, - \, {1 \over - \, (a-b)} \; = \; {2 \over a-b} \, + \, {1 \over a-b} \; = \; {2 \, + \, 1 \over a-b} \; = \; {3 \over a-b} \]
Repetition: Kvadreringsreglerna & konjugatregeln
- \[\begin{align} {\rm 1:a \,\, kvadreringsregeln} \qquad (a+b)^2 & = a^2 + 2\,a\,b + b^2 \\ {\rm 2:a \,\, kvadreringsregeln} \qquad (a-b)^2 & = a^2 - 2\,a\,b + b^2 \\ {\rm \,Konjugatregeln} \qquad (a+b) \cdot (a-b) & = a^2 - b^2 \end{align}\]
OBS! Användningen av reglerna ovan baklänges innebär faktorisering.
Exempel 4
Förenkla uttrycket \( \; {2 \over x^2-4} \, + \, {1 \over 2\,x - x^2} \; \) så långt som möjligt.
Redan i första steget används konjugatregeln baklänges för att faktorisera den första termens nämnare:
\[ {2 \over x^2-4} \, + \, {1 \over 2\,x - x^2} \; = \; {2 \over (x+2)\cdot(x-2)} \, + \, {1 \over (2-x)\cdot x} \; = \; {2 \over (x+2)\cdot(x-2)} \, + \, {1 \, \over - \, (x-2)\cdot x} \; = \; \]
\[ = \; {2 \over (x+2)\cdot(x-2)} \, + \, {-1 \over (x-2)\cdot x} \; = \; {\qquad\quad 2 \qquad\quad\;\cdot {\color{Red} x} \over (x+2)\cdot(x-2) \cdot {\color{Red} x}} \; + \; {{\color{Red} {(x+2)}}\cdot \quad\, (-1) \quad\, \over {\color{Red} {(x+2)}}\cdot (x-2)\cdot x} \; = \; \]
\[ = \; {2\,x \; + \; (x+2) \cdot (-1) \over (x+2) \cdot (x-2)\cdot x} \; = \; {2\,x \; + \; (-x-2) \over (x+2) \cdot (x-2)\cdot x} \; = \; {2\,x - x - 2 \over (x+2) \cdot (x-2)\cdot x} \; = \]
\[ = \; {x - 2 \over (x+2) \cdot (x-2)\cdot x} \; = \; {1 \over x \; (x+2)} \]
Att räkna med rationella uttryck: Multiplikation & division
Även här ska vi använda bråkräkningens regler för att multiplicera och dividera rationella uttryck:
Exempel 1
Förenkla uttrycket \( \; \displaystyle \frac{15}{x^2} \cdot \frac{x}{3} \)
- \[ \;\, {15 \over x^2} \cdot {x \over 3} \; = \; {15 \cdot x \over x^2 \cdot 3} \; =\; {{\color{Red} 3} \cdot 5 \cdot {\color{Blue} x} \over {\color{Blue} x} \cdot x \cdot {\color{Red} 3}} \; = \; {5 \over x} \]
Exempel 2
Förenkla uttrycket \( \; \displaystyle \frac{5\,x^2}{12} \cdot \frac{3}{20\,x} \)
- \[ \;\, {5\,x^2 \over 12} \cdot {3 \over 20\,x} \; = \; {5\,x^2 \cdot 3 \over 12 \cdot 20\,x} \; =\; {{\color{Blue} 5 \cdot x} \cdot x \cdot {\color{Red} 3} \over {\color{Red} 3} \cdot 4 \cdot 4 \cdot {\color{Blue} 5 \cdot x}} \; = \; {x \over 16} \]
Exempel 3
Förenkla uttrycket \( \; \displaystyle \frac{x}{x+3} \cdot \frac{6\,x+18}{6\,x} \; \) så långt som möjligt.
Korrekt lösning: \( \;\, \displaystyle{{x \over x+3} \cdot {6\,x+18 \over 6\,x} \; = \; {x \cdot (6\,x+18) \over (x+3) \cdot 6\,x} \; =\; {x \cdot {\color{Red} 6} \cdot {\color{Blue} (x+3)} \over {\color{Blue} (x+3)} \cdot {\color{Red} 6} \cdot x} \; = \; 1} \)
OBS! Vanligt fel: \( \; \displaystyle{{x \over x+3} \cdot {{\color{Red} {6\,x}}+18 \over {\color{Red} {6\,x}}} \; = \; {x \over x+3} \cdot 18 \; = \; {x \cdot 18 \over x+3} \; =\; {18\,x \over x+3}} \)
Varför är det fel att göra så här?
Det är fel att "förkorta" uttrycket \( \; \displaystyle{{\color{Red} {6\,x}}+18 \over {\color{Red} {6\,x}}} \, \; \) med \( \; {\color{Red} {6\,x}} \; \) därför att \( \; {\color{Red} {6\,x}}+18 \; \) är en summa.
Endast om täljaren och nämnaren är produkter kan gemensamma faktorer förkortas.
Felets förklaring:
Låt oss i uttrycket \( \, \displaystyle{{\color{Red} {6\,x}}+18 \over {\color{Red} {6\,x}}} \, \) anta \( \, x = 1\, \). Felaktig "förkortning" ger \( \, \displaystyle{{\color{Red} 6}+18 \over {\color{Red} 6}} \) \( = 18 \) medan rätt svar är \( \, \displaystyle{{6+18 \over 6} = {24 \over 6}} = 4 \).
Därav följer att vi måste bryta ut \( {\color{Red} 6} \) i uttryckets andra faktor, innan vi kan förkorta:
- \[ {6\,x+18 \over 6\,x} \; =\; {{\color{Red} 6} \cdot (x+3) \over {\color{Red} 6} \cdot x} \; =\; {x+3 \over x} \]
Nu får vi också rätt svar om vi i uttrycket ovan sätter in \( \, x = 1 \): \( \quad \displaystyle{{1+3 \over 1} \, = \, 4} \quad \).
Dvs täljaren \( \, 6\,x+18 \, \) som är en summa måste faktoriseras innan vi kan förkorta.
Exempel 4
I första steget har den 2:a kvadreringsregeln använts baklänges för att faktorisera 2:a gradspolynomet: \( \; x^2 - 2\,x + 1 = (x-1)^2 \, \) för att sedan kunna förkorta med \( (x-1)\, \).
Exempel 5
Förenkla uttrycket \( \; \displaystyle \left(\frac{x^2 - 8\,x + 16}{y^3}\right)\, \Big / \,\left({x - 4 \over y^2}\right) \,\, \; \) så långt som möjligt.
\[ \left({x^2 - 8\,x + 16 \over y^3}\right)\, \Bigg / \,\left({x - 4 \over y^2}\right) \, = \, \left({x^2 - 8\,x + 16 \over y^3}\right)\, \cdot \,\left({y^2 \over x - 4}\right) \, = \, \]
\[ \, = \, {(x^2 - 8\,x + 16) \cdot y^2 \over y^3 \cdot (x - 4)} \, = \, \left\{ {\rm 2\!:\!a\;kvadreringsregeln\;baklänges\!:} \;\, x^2 - 8\,x + 16 = (x-4)^2 \right\} \, = \, \]
\[ \, = \, {(x-4)^2 \cdot y^2 \over y^3 \cdot (x - 4)} \, = \, {(x-4) \cdot {\color{Red} {(x-4)}} \cdot {\color{Red} y} \cdot {\color{Red} y} \over y \cdot {\color{Red} y} \cdot {\color{Red} y} \cdot {\color{Red} {(x - 4)}}} \, = {x-4 \over y} \]
Internetlänkar
http://www03.edu.fi/svenska/laromedel/matematik/nollkurs/pass6.html
http://tutorial.math.lamar.edu/Classes/Alg/RationalExpressions.aspx
http://www.youtube.com/watch?v=FZdt73khrxA&feature=channel
http://www.youtube.com/watch?v=hVIol-6vocY&feature=related </big>
Copyright © 2011-2016 Taifun Alishenas. All Rights Reserved.