Skillnad mellan versioner av "Diagnosprov kap 4 och 5 Integraler och Trigonometri"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 20: | Rad 20: | ||
<big> | <big> | ||
[[Image: Diagnosprov_Ma3c_Integraler_Trigonometri_2_920.jpg]] | [[Image: Diagnosprov_Ma3c_Integraler_Trigonometri_2_920.jpg]] | ||
| − | [[Image: | + | [[Image: Diagnosprov_Ma3c_Integraler_Trigonometri_3_920.jpg]] |
<br> | <br> | ||
'''Ledning till fråga 13:''' | '''Ledning till fråga 13:''' | ||
Versionen från 1 april 2017 kl. 16.09
| Diagnosprov kap 4 & 5 som PDF | Lösningar till diagnosprov kap 4/5 | Formelsamling Trigonometri | Formelsamling Integraler | Kap 4 Integraler |
| Kap 5 Trigonometri |
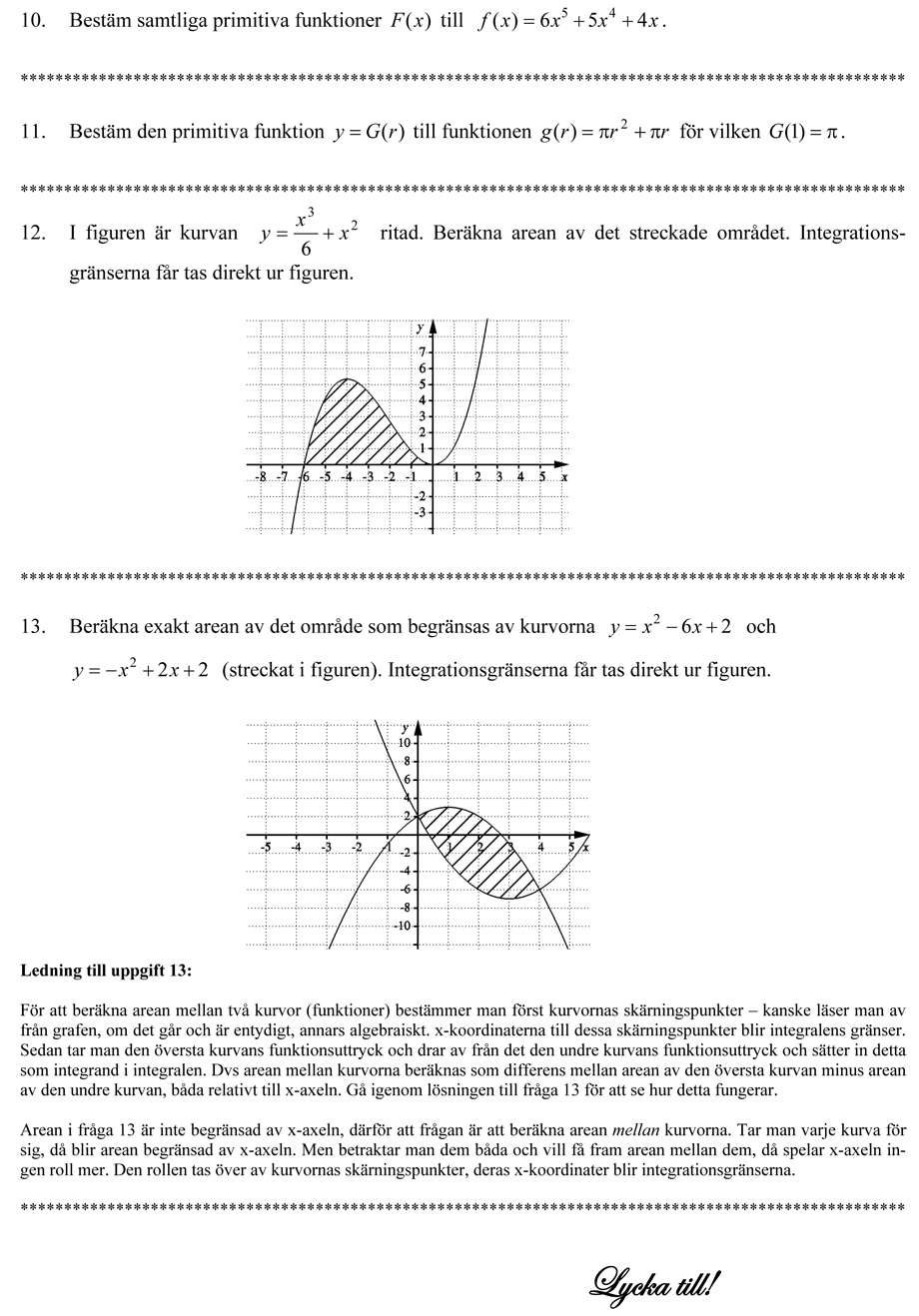
För att beräkna arean mellan två kurvor (funktioner) bestämmer man först kurvornas skärningspunkter – kanske läser man av från grafen, om det går och är entydigt, annars algebraiskt. x-koordinaterna till dessa skärningspunkter blir integralens gränser. Sedan tar man den översta kurvans funktionsuttryck och drar av från det den undre kurvans funktionsuttryck och sätter in detta som integrand i integralen. Dvs arean mellan kurvorna beräknas som differens mellan arean av den översta kurvan minus arean av den undre kurvan, båda relativt till x-axeln. Gå igenom lösningen till fråga 13 för att se hur detta fungerar.
Arean i fråga 13 är inte begränsad av x-axeln, därför att frågan är att beräkna arean mellan kurvorna. Tar man varje kurva för sig, då blir arean begränsad av x-axeln. Men betraktar man dem båda och vill få fram arean mellan dem, då spelar x-axeln ingen roll mer. Den rollen tas över av kurvornas skärningspunkter, deras x-koordinater blir integrationsgränserna.
Copyright © 2011-2017 Taifun Alishenas. All Rights Reserved.