Skillnad mellan versioner av "Diagnosprov kap 4 och 5 Integraler och Trigonometri"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 18: | Rad 18: | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| − | + | ||
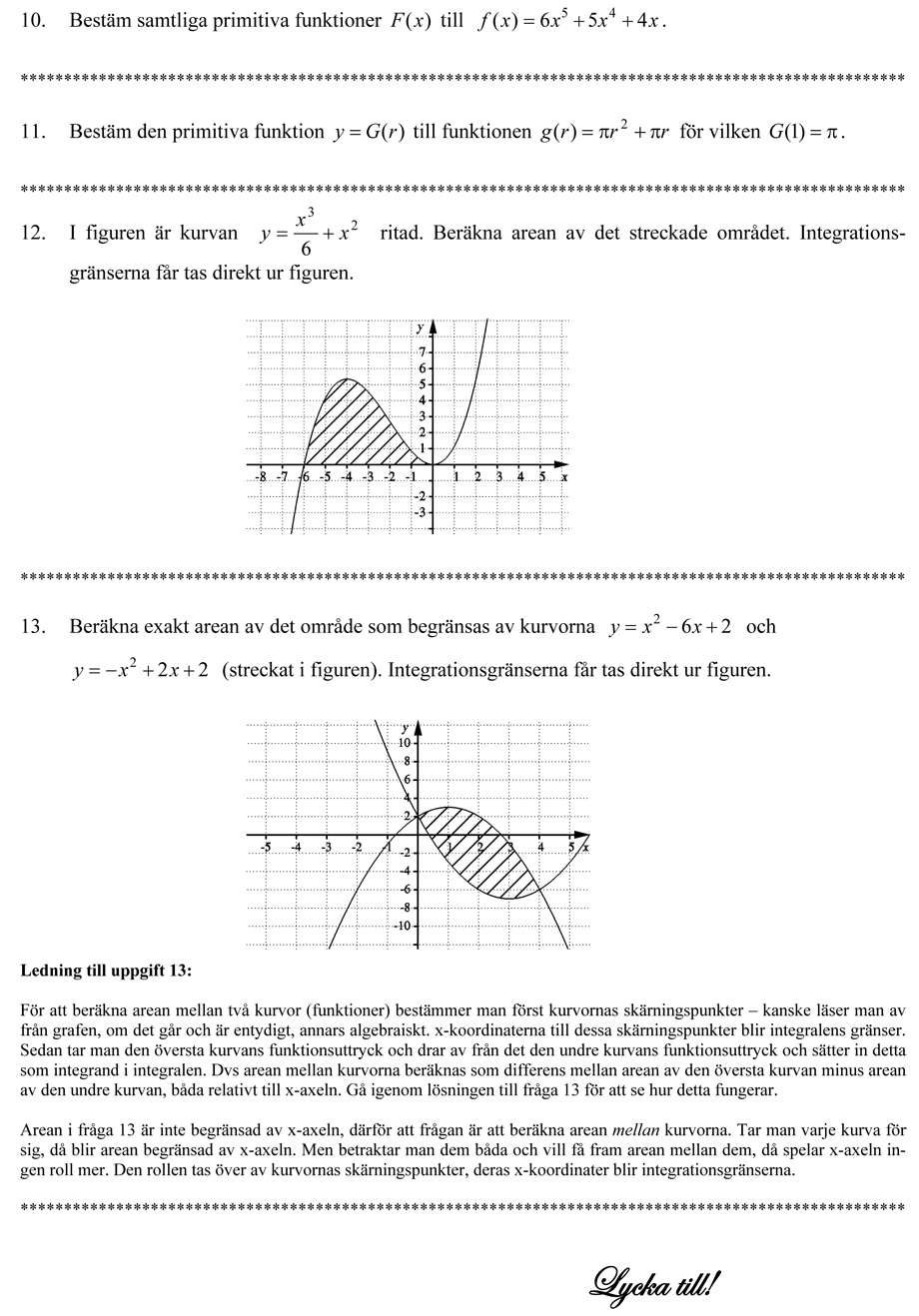
[[Image: Diagnosprov_Ma3c_Integraler_Trigonometri_2_920.jpg]] | [[Image: Diagnosprov_Ma3c_Integraler_Trigonometri_2_920.jpg]] | ||
[[Image: Diagnosprov_Ma3c_Integraler_Trigonometri_3_920.jpg]] | [[Image: Diagnosprov_Ma3c_Integraler_Trigonometri_3_920.jpg]] | ||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ||
Versionen från 1 april 2017 kl. 16.11
| Diagnosprov kap 4 & 5 som PDF | Lösningar till diagnosprov kap 4/5 | Formelsamling Trigonometri | Formelsamling Integraler | Kap 4 Integraler |
| Kap 5 Trigonometri |
Copyright © 2011-2017 Taifun Alishenas. All Rights Reserved.