Skillnad mellan versioner av "2.2 Genomsnittlig förändringshastighet"
Taifun (Diskussion | bidrag) m (→Exempel 2) |
Taifun (Diskussion | bidrag) m (→Exempel 2) |
||
| Rad 85: | Rad 85: | ||
c) Beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet <math> 20 \leq x \leq 30 </math>. | c) Beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet <math> 20 \leq x \leq 30 </math>. | ||
| − | d) När är oljans genomsnittliga utströmningshastighet störst? Ange den så noggrant | + | d) När är oljans (genomsnittliga) utströmningshastighet störst? Ange den så noggrant som möjligt. |
'''Lösning''': | '''Lösning''': | ||
| Rad 111: | Rad 111: | ||
I tidsintervallet <math> 20 \leq x \leq 30 </math> sjunker oljans volym med 180 liter per minut. | I tidsintervallet <math> 20 \leq x \leq 30 </math> sjunker oljans volym med 180 liter per minut. | ||
| + | |||
| + | d) Grafen i a) visar att kurvans lutning är störst i början dvs vid tiden <math> x = 0\, </math> när oljan har mest volym, nämligen 9 000 liter. Därför är även oljans utströmningshastighet störst vid denna tidpunkt. Men denna hastighet är inte längre genomsnittlig (i något intervall) utan momentan. | ||
| + | |||
| + | För att beräkna den momentana och därmed den exakta utströmningshastigheten vid tiden <math> x = 0\, </math> måste man bestämma funktionen <math> y\, </math>:s exakta derivata. För att approximera denna momentana utströmningshastighet så noggrant som möjligt måste vi välja ett så litet tidsintervall som möjligt med <math> x = 0\, </math> som undre intervallgräns. | ||
| + | |||
| + | Låt oss t.ex. beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet <math> 0 \leq x \leq 0,1 </math>: | ||
Versionen från 30 april 2011 kl. 22.10
| Teori | Övningar |
Vad är genomsnittlig förändringshastighet?
Givet:
- Funktionen \( y \, = \, f\,(x) \) i form av en formel, tabell eller graf.
- Något intervall på \( x\, \)-axeln\[ x_1 \,\leq\, x \,\leq\, x_2 \] dvs ett intervall med givna gränser \( x_1\, \) och \( x_2\, \).
Sökt:
- Funktionens genomsnittliga förändringshastighet i detta intervall dvs:
- \[ {\Delta y \over \Delta x} \; = \; {y_2 - y_1 \over x_2 - x_1} \; = \; {f(x_2) \, - \, f(x_1) \over x_2 - x_1} \]
En annan form på den genomsnittliga förändringshastigheten får man om man inför den nya beteckningen \( h\, \) för intervallets längd:
- \[\begin{align} h & = x_2 - x_1 \qquad & | \; + \; x_1 \\ x_1 + h & = x_2 \\ \end{align}\]
Då kan funktionen \( y = f\,(x) \):s genomsnittliga förändringshastighet i intervallet \( x_1 \,\leq\, x \,\leq\, x_1 + h \) definieras som:
- \[ {\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h} \]
Vilket av de två identiska uttrycken ovan man använder beror på sammanhanget. I rent beräkningssammanhang föredras ofta den första formen, medan man i teoretiska resonemang, speciellt när man definierar derivatan exakt eller bevisar deriveringsregler, snarare använder sig av den andra formen.
Kärt barn har många namn: De två uttrycken ovan har ett antal namn som allihopa kan anses vara synonymer:
- Genomsnittlig förändringshastighet
- Förändringskvot
- Ändringskvot
- Differenskvot
Om vi kommer ihåg hur begreppet lutning till en rät linje var definierat i Matte B-kursen, kan vi säga att uttrycket ovan (ta den första formen) är inget annat än lutningen till den räta linje som ersätter kurvan \( y = f\,(x) \) i det betraktade intervallet. Dvs om man bortser från kurvans verkliga (kanske krokiga) förlopp och antar istället att det går en rät linje i det betraktade intervallet kan denna räta linjes lutning beräknas med uttrycket ovan. Den räta linjens lutning kallas då kurvans genomsnittliga förändringshastighet i det betraktade intervallet.
Exempel 1
Givet:
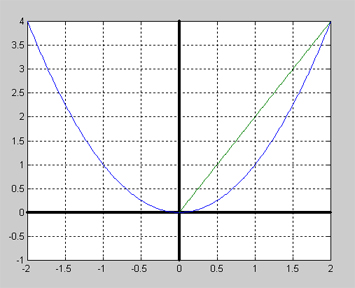
- Funktionen \( y \, = \, x^2 \)
- Intervallet \( 0 \,\leq\, x \,\leq\, 2 \)
Sökt:
- Funktionens genomsnittliga förändringshastighet i detta intervall.
Lösning:
- \[ {\Delta y \over \Delta x} \; = \; {f(2) \, - \, f(0) \over 2 - 0} \; = \; {2^2 \, - \, 0^2 \over 2 - 0} \; = \; {4 \, - \, 0 \over 2} \; = \; {4 \over 2} \; = \; 2 \]
Funktionen \( y = x^2 \, \) växer i intervallet \( 0 \leq x \leq 2 \) med 2 y-enheter per x-enhet. Detta är innebörden av att funktionens genomsnittliga förändringshastighet i detta intervall är 2.
Ersätter man i detta intervall kurvan med en rät linje, är linjens lutning som är 2 identisk med kurvans genomsnittliga förändringshastighet.
Exempel 2
En oljetank läcker genom ett hål i tankens botten. Utströmningen av oljan beskrivs av funktionen:
- \[ y \, = \, 4\,x^2 - 380\,x + 9\,000 \]
där
- \[ y \, = \, \] Oljans volym i liter
- \[ x \, = \, \] Tiden i minuter
a) Rita grafen till funktionen som beskriver utströmningen.
b) Hur stor är oljans genomsnittliga utströmningshastighet i hela tidsintervallet från början tills tanken är tom.
c) Beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet \( 20 \leq x \leq 30 \).
d) När är oljans (genomsnittliga) utströmningshastighet störst? Ange den så noggrant som möjligt.
Lösning:
a)
b) Grafen tyder pår att tanken är tom efter ca. 45 minuter. Den exakta tiden får man genom att lösa 2:a gradsekvationen:
- \[ 4\,x^2 - 380\,x + 9\,000 = 0 \]
Räknarens ekvationslösare visar att \( x = 45\, \) är den exakta tiden. Därför är hela tidsintervallet från början tills tanken är tom \( 0 \leq x \leq 45 \). I detta intervall är oljans genomsnittliga utströmningshastighet:
- \[ {\Delta y \over \Delta x} = {f(45) \, - \, f(0) \over 45 - 0} = {0 \, - \, 9000 \over 45} = {-9000 \over 45} = -200 \]
I hela tidsintervallet \( 0 \leq x \leq 45 \) sjunker oljans volym med 200 liter per minut.
c) I tidsintervallet \( 20 \leq x \leq 30 \) är oljans genomsnittliga utströmningshastighet\[ f\,(30) = 4 \cdot 30^2 - 380 \cdot 30 + 9\,000 = 1200 \]
\( f\,(20) = 4 \cdot 20^2 - 380 \cdot 20 + 9\,000 = 3000 \)
\( {\Delta y \over \Delta x} = {f(30) \, - \, f(20) \over 30 - 20} = {1200 \, - \, 3000 \over 30 - 20} = {-1800 \over 10} = -180 \)
I tidsintervallet \( 20 \leq x \leq 30 \) sjunker oljans volym med 180 liter per minut.
d) Grafen i a) visar att kurvans lutning är störst i början dvs vid tiden \( x = 0\, \) när oljan har mest volym, nämligen 9 000 liter. Därför är även oljans utströmningshastighet störst vid denna tidpunkt. Men denna hastighet är inte längre genomsnittlig (i något intervall) utan momentan.
För att beräkna den momentana och därmed den exakta utströmningshastigheten vid tiden \( x = 0\, \) måste man bestämma funktionen \( y\, \):s exakta derivata. För att approximera denna momentana utströmningshastighet så noggrant som möjligt måste vi välja ett så litet tidsintervall som möjligt med \( x = 0\, \) som undre intervallgräns.
Låt oss t.ex. beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet \( 0 \leq x \leq 0,1 \):