Skillnad mellan versioner av "2.7 Numerisk derivering"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 19: | Rad 19: | ||
Numerisk derivering är en metod för approximativ (ungefärlig) beräkning av derivatan. Med hjälp av numeriska deriveringsformler beräknas ett <strong><span style="color:red">närmevärde</span></strong> för derivatan. | Numerisk derivering är en metod för approximativ (ungefärlig) beräkning av derivatan. Med hjälp av numeriska deriveringsformler beräknas ett <strong><span style="color:red">närmevärde</span></strong> för derivatan. | ||
| − | Frågan uppstår: varför ska vi ta fram ett närmevärde när vi kan få derivatans exakta värde med hjälp av de [[2. | + | Frågan uppstår: varför ska vi ta fram ett närmevärde när vi kan få derivatans exakta värde med hjälp av de [[2.5_Deriveringsregler|<strong><span style="color:blue">deriveringsregler</span></strong>]] vi ställde upp i de två sista avsnitten? Svaret är: Det finns typer av funktioner som inte matchar någon av de deriveringsregler vi lärt oss. Det finns t.o.m. typer av funktioner som inte har någon deriveringsregel alls. Eller det är i praktiken svårt <math>-</math> ibland kanske onödigt <math>-</math> att beräkna derivatan exakt. Men i vilka situationer ska man använda numerisk derivering? |
Vi ska titta på den numeriska deriveringens användningsområden: | Vi ska titta på den numeriska deriveringens användningsområden: | ||
Versionen från 7 november 2014 kl. 07.37
| <-- Förra avsnitt | Teori | Övningar | Diagnosprov kap 2 Derivatan | Lösningar till diagnosprov kap 2 |
Innehåll
Varför numerisk derivering?
Numerisk derivering är en metod för approximativ (ungefärlig) beräkning av derivatan. Med hjälp av numeriska deriveringsformler beräknas ett närmevärde för derivatan.
Frågan uppstår: varför ska vi ta fram ett närmevärde när vi kan få derivatans exakta värde med hjälp av de deriveringsregler vi ställde upp i de två sista avsnitten? Svaret är: Det finns typer av funktioner som inte matchar någon av de deriveringsregler vi lärt oss. Det finns t.o.m. typer av funktioner som inte har någon deriveringsregel alls. Eller det är i praktiken svårt \(-\) ibland kanske onödigt \(-\) att beräkna derivatan exakt. Men i vilka situationer ska man använda numerisk derivering?
Vi ska titta på den numeriska deriveringens användningsområden:
- 1) När vi ska derivera t.ex. följande funktion konstaterar vi att den inte matchar med någon funktionstyp i vår deriveringstabell. Den kan inte deriveras med någon av de deriveringsregler vi känner till hittills:
- \[ f(x) = {1 \over x + 1} \]
- Först i Matte 4-kursen lär man sig den s.k. kvotregeln med vars hjälp en kvot (resultat av en division) av två funktioner kan deriveras.
- Ett annat exempel är \( f(x) = \ln x\, \) som inte heller matchar mot någon funktionstyp i vår deriveringstabell och vars numerisk derivering visas i Exempel 2 längre fram.
- 2) När vi har en funktion vars derivata blir så komlicerad att det tar mer tid att ställa upp den än att genomföra numerisk derivering. Exempel:
- \[ f(x) = {\sin\,3\,x \over 4\,\cos\,x} \]
- \[ f\,'(x) = {12\,\cos\,3\,x \cdot \cos\,x \,+\, 4\,\sin\,3\,x \cdot \sin\,x \over 16\,\cos^2\,x} \]
- För det första är det inte enkelt att ställa upp \( f\,'(x) \). Även detta görs med kvotregeln som vi inte känner till.
- För det andra ser man att det är väsentligt enklare att beräkna t.ex. \( f(2)\, \) än \( f\,'(2) \). I de numeriska deriveringsformlerna ingår nämligen endast beräkningar av \( f(x)\, \), inte av \( f\,'(x) \).
- 3) När vi ska derivera en funktion som saknar algebraisk formel och är endast given i tabellform, dvs numeriskt. Pga avsaknaden av en formel finns det ingen annan möjlighet att derivera den än numerisk derivering. Ett exempel:

- Sådana funktioner förekommer ofta som resultat av mätdata utan någon formel. Ändå uppfyller de definitionen på en funktion, nämligen att vara en
- "Regel som tilldelar varje \( x\, \)-värde endast ett \( y\, \)-värde."
Det finns en uppsjö av numeriska deriveringsformler. Vi behandlar i detta avsnitt de tre enklaste:
- Framåtdifferenskvoten
- Bakåtdifferenskvoten
- Centrala differenskvoten
Framåtdifferenskvoten
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Framåtdifferenskvoten:
\[ f\,'(a) \qquad \approx \qquad {f(a + h) \, - \, f(a) \over h} \qquad {\color{White} x} \]
- Tangentens lutning \( {\color{White} x} \approx \quad {\color{White} x} \) Sekanten F:s lutning
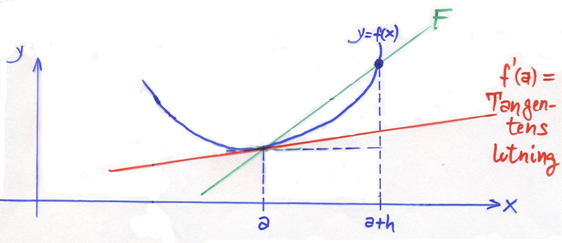
\( h\, \) kallas steglängden. Approximationen är desto bättre ju mindre steglängden är.
Exempel 1
Givet:
- Följande funktion \( f(x)\, \) i tabellform:
\( x\, \) \( f(x)\, \) \( 0,5\, \) \( 1,79744\, \) \( 0,6\, \) \( 2,04424\, \) \( 0,7\, \) \( 2,32751\, \)
Sökt:
- Funktionens derivata i \( x = 0,6\, \) dvs \( f\,'(0,6) \) med framåtdifferenskvoten.
Lösning:
- Steglängden \( h = 0,1\, \) är given i tabellen.
- \[ f\,'(0,6) = {f(0,6 + 0,1) - f(0,6) \over 0,1} = {f(0,7) - f(0,6) \over 0,1} = {2,32751 - 2,04424 \over 0,1} = {0,28327 \over 0,1} = 2,8327 \]
Bakåtdifferenskvoten
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Bakåtdifferenskvoten:
\[ f\,'(a) \qquad \approx \qquad {f(a) \, - \, f(a-h) \over h} \qquad {\color{White} x} \]
- Tangentens lutning \( {\color{White} x} \approx \quad {\color{White} x} \) Sekanten B:s lutning
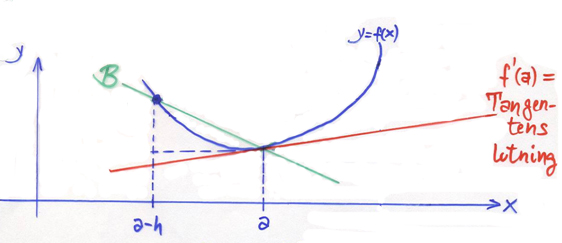
Även här gäller att approximationen är desto bättre ju mindre steglängden \( h\, \) är.
Exempel 2
Givet:
- Funktionen \( f(x) = \ln x\, \)
- Steglängden \( h = 0,01\, \)
Sökt:
- Funktionens derivata i \( x = 1,8\, \) dvs \( f\,'(1,8) \) med bakåtdifferenskvoten .
Lösning:
\[ f\,'(1,8) \approx {f(1,8) - f(1,8 - 0,01) \over 0,01} = {f(1,8) - f(1,79) \over 0,01} = {\ln(1,8) - \ln(1,79) \over 0,01} = 0,5571 \]
Det exakta värdet avrundat till 4 decimaler är \( f\,'(1,8) = 0,5556\, \).
Centrala differenskvoten
Derivatan \( f\,'(a) \) av funktionen \( y = f\,(x) \) i punkten \( x = a\, \) kan approximeras med Centrala differenskvoten:
\[ f\,'(a) \qquad \approx \qquad {f(a + h) \, - \, f(a-h) \over 2\,h} \qquad {\color{White} x} \]
- Tangentens lutning \( {\color{White} x} \approx \quad {\color{White} x} \) Sekanten C:s lutning
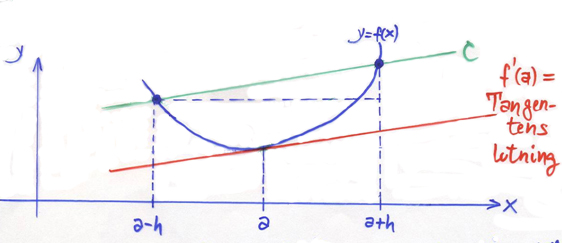
Approximationen är desto bättre ju mindre \( h\, \) är.
Exempel 3
Givet:
- Funktionen \( f(x) = x\,^2 \)
- Steglängden \( h = 0,5\, \)
Sökt:
- Funktionens derivata i \( x = 1\, \) dvs \( f\,'(1) \) med centrala differenskvoten .
Lösning:
- \[ f\,'(1) \approx {f(1 + 0,5) - f(1 - 0,5) \over 2\cdot 0,5} = {f(1,5) - f(0,5) \over 2\cdot 0,5} = {1,5^2 - 0,5^2 \over 1} = 2 \]
Funktionens derivata är \( f\,'(x) = 2\,x \) och därmed det exakta värdet \( f\,'(1) = 2 \cdot 1 = 2 \).
Noggrannhetsbedömning
Är det en slump att den numeriska deriveringen med centrala differenskvoten i Exempel 3 ger exakt värde, fast steglängden är relativt stor?
Svaret är nej: Den centrala differenskvoten deriverar alla 2:a gradsfunktioner (och förstås även alla 1:a gradsfunktioner) exakt oberoende av steglängden. Här följer beviset:
Sats:
- Den centrala differenskvoten ger den exakta derivatan till alla 2:a gradsfunktioner oberoende av steglängden.
- Om \( f(x) \; = \; x^2 \)
- då:
- \[ {f(x + h) \, - \, f(x-h) \over 2\,h} \; = \; 2\,x \]
Bevis:
\[ {f(x + h) - f(x-h) \over 2\,h} = {(x+h)^2 - (x-h)^2 \over 2\,h} = {(x^2 + 2\,x\,h + h^2) - (x^2 - 2\,x\,h + h^2) \over 2\,h} = \]
\[ = {x^2 + 2\,x\,h + h^2 - x^2 + 2\,x\,h - h^2 \over 2\,h} = {4\,x\,h \over 2\,h} = 2\,x = f\,'(x) \]
Det räcker att bevisa satsen för \( f(x) = x^2\, \) som an slags representant för alla 2:a gradsfunktioner, eftersom \( x^2\, \) är den avgörande termen för 2:a gradsfunktioner.
Självfallet går det att bevisa satsen även för \( f(x) = a\,x^2 + b\,x + c \). Det tar bara lite längre att räkna.
Resultatet är det samma: Den centrala differenskvoten deriverar alla 2:a gradsfunktioner exakt. Att detta är oberoende av steglängden visas i beviset ovan genom att \( h\, \) förkortas bort i slutet.
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.