Skillnad mellan versioner av "3.2 Lokala maxima och minima"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 14: | Rad 14: | ||
| − | == | + | == Regel om maxima och minima med andraderivata == |
<span style="color:white">:</span> | <span style="color:white">:</span> | ||
| Rad 100: | Rad 100: | ||
Alltså är nattens lägsta temperatur <math> 1 \, </math> grad Celsius. | Alltså är nattens lägsta temperatur <math> 1 \, </math> grad Celsius. | ||
| + | |||
| + | |||
| + | == Regel om maxima och minima med teckentabell == | ||
| + | |||
| + | <span style="color:white">:</span> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 15px;padding:10px 20px 10px 20px;-webkit-border-radius: 15px;"> | ||
| + | <big>'''Derivatans nollställen och dess teckenbyte avgör för vilka <math>\, x </math> en funktion har maxima och minima''': | ||
| + | |||
| + | |||
| + | Funktionen <math> {\color{White} x} y \, = \, f(x) {\color{White} x} </math> har ett <strong><span style="color:red">maximum</span></strong> i <math> {\color{White} x} x = a {\color{White} x} </math> om derivatan <math> {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} </math> och derivatan byter förtecken från <math> {\color{White} x} - {\color{White} x} </math> till <math> {\color{White} x} + {\color{White} x} </math>. | ||
| + | ---- | ||
| + | Funktionen <math> {\color{White} x} y \, = \, f(x) {\color{White} x} </math> har ett <strong><span style="color:red">minimum</span></strong> i <math> {\color{White} x} x = a {\color{White} x} </math> om derivatan <math> {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} </math> och derivatan byter förtecken från <math> {\color{White} x} + {\color{White} x} </math> till <math> {\color{White} x} - {\color{White} x} </math>. | ||
| + | </big></div> | ||
| + | |||
| + | |||
| + | Vi tar samma exempel som ovan (Vinternattens kallaste tidpunkt), men byter metod: Vi använder inte längre andraderivatan utan en teckentabell som nöjer sig med första derivatan. | ||
Versionen från 20 november 2014 kl. 12.13
| <-- Förra avsnitt | Teori | Övningar | --> Nästa avsnitt |
Innehåll
Regel om maxima och minima med andraderivata
:
Derivatans nollställen och andraderivatans förtecken avgör för vilka \(\, x \) en funktion har maxima och minima:
Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett maximum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och andraderivatan \( {\color{White} x} f\,''(a) \, {\bf {\color{Red} <}} \, 0 {\color{White} x}. \)
Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett minimum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och andraderivatan \( {\color{White} x} f\,''(a) \, {\bf {\color{Red} >}} \, 0 {\color{White} x}. \)
Med andraderivatan menas derivatans derivata. Man får andraderivatan genom att derivera derivatans funktion en gång till.
Med derivatan menas alltid första derivatan. Med maximum menas en funktions största och med minimum en funktions minsta värde.
| Regeln ovan säger i ord:
|
Där derivatan är \( \, 0 \) och andraderivatan är negativ har funktionen ett maximum.
Där derivatan är \( \, 0 \) och andraderivatan är positiv har funktionen ett minimum. |
I exemplet nedan behandlas en funktion vars graf visar ett minimum. En algebraisk metod används för att med regeln ovan hitta detta minimum dvs beräkna det \(\, x \) för vilket funktionen antar sitt minimum. Med detta \(\, x \) beräknas sedan funktionens minsta värde.
Exempel 1 Vinternattens kallaste tidpunkt
Vi återgår till Exempel 1 i förra avsnitt, men byter frågeställning: Vi tittar inte längre på funktionens växande eller avtagande utan på funktionens minsta värde (minimum):
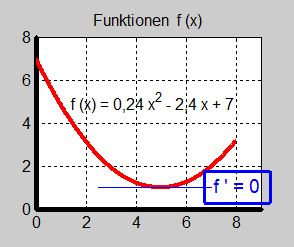
Under en vinternatt varierar temperaturen enligt funktionen \( {\color{White} x} \; y \, = \, f(x) \, = \, 0,24\,x^2\,-\,2,4\,x\,+\,7 {\color{White} x} \; \) med definitionsområdet: \( \quad 0 \leq x \leq 8 \).
där \( y \; = \) temperaturen i grader Celsius och
\( x \; = \) tiden i timmar efter midnatt
a) Bestäm nattens kallaste tidpunkt.
b) Bestäm nattens lägsta temperatur.
Lösning:
a) För att kunna använda reglerna om maxima och minima ställer vi upp första- och andraderivatan:
- \[ f(x) \, = \, 0,24\,x^2 - 2,4\,x + 7 \]
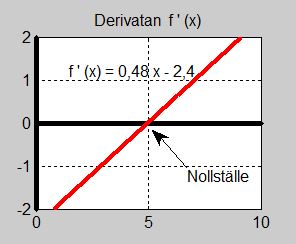
- \[ f'(x) \, = \, 0,48\,x - 2,4 \]
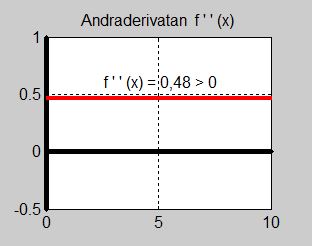
- \[ f''(x) \, = \, 0,48 \]
Graferna till dessa tre funktioner visas ovan.
För att få reda på derivatans nollställe som regeln kräver sätter vi derivatan till \( \, 0 \) och beräknar tidpunkten \( x \, \) då derivatan blir \( \, 0 \):
- \[\begin{array}{rcrcl} f'(x) & = & 0,48\,x - 2,4 & = & 0 \\ & & 0,48\,x & = & 2,4 \\ & & x & = & {2,4 \over 0,48} \\ & & x & = & 5 \end{array}\]
Nu vet vi att derivatan blir \( \, 0 \) i \( x = 5 \, \) dvs tangenten till kurvan \( y = f(x) \, \) är horisontell i \( x = 5 \, \). Men en horisontell tangent kan vara ett maximum eller ett minimum.
För att avgöra om det föreligger ett maximum eller ett minimum kräver regeln andraderivatans förtecken. Därför sätter vi \( x = 5 \, \) in i andraderivatan och kollar om den blir positiv eller negativ:
- \[ f''(5) = 0,48 \,>\, 0 \]
Andraderivatan är positiv (konstant) för alla \( x \, \) och därmed även för \( x = 5 \, \). Därav följer att \( f(x) \, \) har ett minimum i \( x = 5 \, \).
Alltså är nattens kallaste tidpunkt kl \( 5 \, \).
b) Temperaturen vid kl \( 5 \, \) är:
- \[ f(5) = 0,24 \cdot 5^2 - 2,4 \cdot 5 + 7 = 1 \]
Alltså är nattens lägsta temperatur \( 1 \, \) grad Celsius.
Regel om maxima och minima med teckentabell
:
Derivatans nollställen och dess teckenbyte avgör för vilka \(\, x \) en funktion har maxima och minima:
Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett maximum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och derivatan byter förtecken från \( {\color{White} x} - {\color{White} x} \) till \( {\color{White} x} + {\color{White} x} \).
Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett minimum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och derivatan byter förtecken från \( {\color{White} x} + {\color{White} x} \) till \( {\color{White} x} - {\color{White} x} \).
Vi tar samma exempel som ovan (Vinternattens kallaste tidpunkt), men byter metod: Vi använder inte längre andraderivatan utan en teckentabell som nöjer sig med första derivatan.