Skillnad mellan versioner av "3.4 Kurvkonstruktioner"
Från Mathonline
Taifun (Diskussion | bidrag) m (→Globala maxima och minima) |
Taifun (Diskussion | bidrag) m (→Globala maxima och minima) |
||
| Rad 36: | Rad 36: | ||
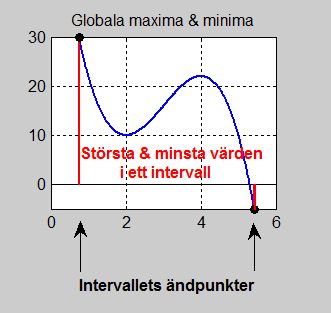
På bilden till vänster är funktionens största värde <math> \, 30 \, </math> och dess minsta | På bilden till vänster är funktionens största värde <math> \, 30 \, </math> och dess minsta | ||
| − | värde <math> \, -5 \, </math> (OBS! <math> \, y</math>-värden). | + | värde <math> \, -5 \, </math> (OBS! <math> \, y</math>-värden). De visas med <big><big><big>•</big></big></big> . |
| − | + | ||
| − | + | ||
Versionen från 15 januari 2015 kl. 13.15
| <-- Förra avsnitt | Teori | Övningar | --> Nästa avsnitt |
Innehåll
Fortfarande förutsätts att alla funktioner \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) vi behandlar här är kontinuerliga i alla punkter av det betraktade området.
Globala maxima och minima
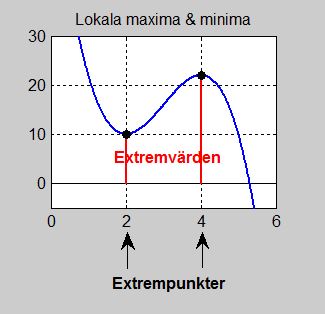
I avsnittet om Lokala maxima och minima hade vi tittat på sådana punkter som hade maximala och minimala \( \, y\)-värden i sin närmaste omgivning, därför "lokala", se bilden till höger.
I detta avsnitt ska vi betrakta sådana punkter som har största och minsta \( \, y\)-värden i ett intervall, därför "globala", se bilden till vänster.
I praktiken hittar man en funktions globala extrema genom att:
- Hitta funktionens lokala extrema med någon av de regler vi lärde oss i förra avsnitt (andraderivatan eller teckenstudium).
- Beräkna de lokala extremvärdena.
- Beräkna funktionsvärdena i definitionsintervallets ändpunkter.
- Jämföra de lokala extremvärdena med värdena i definitionsintervallets ändpunkter.
Globalt extremum saknas
En problematik som kan dyka upp när man är ute efter globala extrema är att de inte existerar.