Skillnad mellan versioner av "3.4 Kurvkonstruktioner"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 10: | Rad 10: | ||
[[Media: Lektion 32 Kurvkonstruktioner Ruta.pdf|<strong><span style="color:blue">Lektion 32 Kurvkonstruktioner</span></strong>]] | [[Media: Lektion 32 Kurvkonstruktioner Ruta.pdf|<strong><span style="color:blue">Lektion 32 Kurvkonstruktioner</span></strong>]] | ||
| + | __NOTOC__ <!-- __TOC__ --> | ||
| + | <div class="tolv"> <!-- tolv1 --> | ||
| + | Fortfarande förutsätts att alla funktioner <math> {\color{White} x} y \, = \, f(x) {\color{White} x} </math> vi behandlar här är [[1.5_Kontinuerliga_och_diskreta_funktioner|<strong><span style="color:blue">kontinuerliga</span></strong>]] i alla punkter av det betraktade området. | ||
| + | </div> <!-- tolv1 --> | ||
| − | + | == <b><span style="color:#931136">Översikt över punkter som kan identifieras med derivator <math>-</math> en sammanfattning av de två förra avsnitten</span></b> == | |
| + | [[Image: Oversikt Punkter_62_Ph.jpg]] | ||
| − | |||
| − | + | <Big><Big> Med Min och Max i översikten ovan menas lokal minimi- och maximipunkt.</Big></Big> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | == | + | == <b><span style="color:#931136">Största och minsta värden: globala maxima och minima</span></b> == |
I avsnittet om [[3.2_Lokala_maxima_och_minima|<strong><span style="color:blue">Lokala maxima och minima</span></strong>]] hade vi tittat på sådana punkter som hade maximala och minimala <math> \, y</math>-värden i sin närmaste omgivning, därför "lokala", se bilden till höger. | I avsnittet om [[3.2_Lokala_maxima_och_minima|<strong><span style="color:blue">Lokala maxima och minima</span></strong>]] hade vi tittat på sådana punkter som hade maximala och minimala <math> \, y</math>-värden i sin närmaste omgivning, därför "lokala", se bilden till höger. | ||
| Rad 61: | Rad 62: | ||
| + | <div class="exempel12"> <!-- exempel12 --> | ||
I praktiken hittar man en funktions globala extrema genom att: | I praktiken hittar man en funktions globala extrema genom att: | ||
| − | # Hitta funktionens lokala extrema med någon av de regler vi lärde oss i förra avsnitt ([[3. | + | # Hitta funktionens lokala extrema med någon av de regler vi lärde oss i förra avsnitt ([[3.2_Lokala_maxima_och_minima#Regler_om_maxima_och_minima_med_andraderivata|<strong><span style="color:blue">andraderivatan</span></strong>]] eller [[3.2_Lokala_maxima_och_minima#Regler_om_maxima_och_minima_med_teckenstudium|<strong><span style="color:blue">teckenstudium</span></strong>]]). |
# Beräkna de lokala extremvärdena. | # Beräkna de lokala extremvärdena. | ||
# Beräkna funktionsvärdena i definitionsintervallets ändpunkter. | # Beräkna funktionsvärdena i definitionsintervallets ändpunkter. | ||
# Jämföra de lokala extremvärdena med värdena i definitionsintervallets ändpunkter. | # Jämföra de lokala extremvärdena med värdena i definitionsintervallets ändpunkter. | ||
| + | </div> <!-- exempel12 --> | ||
| − | == | + | == <b><span style="color:#931136">När saknas globalt extremum?</span></b> == |
| − | + | <div class="tolv"> <!-- tolv2 --> | |
En funktion behöver inte nödvändigtvis ha extrema, varken lokala eller globala. | En funktion behöver inte nödvändigtvis ha extrema, varken lokala eller globala. | ||
| − | Detta kan hända | + | Detta kan hända när man letar efter globala extrema där man förväntar dem, t.ex. i definitionsintervallets ändpunkter. Det ser ut så <math>-</math> t.ex. i grafen <math>-</math> som om funktionen antog sina största (eller minsta) värden i intervallets ändpunkter. Att det inte behöver vara så visar följande exempel: |
| + | </div> <!-- tolv2 --> | ||
| + | |||
| + | <div class="exempel"> <!-- exempel2 --> | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td> | ||
'''Exempel:''' | '''Exempel:''' | ||
| Rad 81: | Rad 90: | ||
<math> y \, = \, f(x) \, = \, x^2 \quad </math> Definitionsmängden<span style="color:black">:</span> <math> \quad -2 < x < 2 </math> | <math> y \, = \, f(x) \, = \, x^2 \quad </math> Definitionsmängden<span style="color:black">:</span> <math> \quad -2 < x < 2 </math> | ||
| − | |||
| − | |||
| − | |||
Av någon anledning är intervallets ändpunkter inte inkluderade i definitionsmängden. | Av någon anledning är intervallets ändpunkter inte inkluderade i definitionsmängden. | ||
| Rad 108: | Rad 114: | ||
-webkit-border-radius: 10px;"><strong>Globalt maximum saknas.</strong></div> | -webkit-border-radius: 10px;"><strong>Globalt maximum saknas.</strong></div> | ||
</td> | </td> | ||
| − | <td> [[Image: Globala extrema saknas.jpg]]</td> | + | <td> [[Image: Globala extrema saknas.jpg]]</td> |
</tr> | </tr> | ||
</table> | </table> | ||
| + | </div> <!-- exempel2 --> | ||
| + | |||
| + | |||
| + | <div class="tolv"> <!-- tolv3 --> | ||
Att globalt maximum saknas har inte med funktionens egenskaper att göra utan snarare med intervallets där <math> f(x) </math> är definierad. | Att globalt maximum saknas har inte med funktionens egenskaper att göra utan snarare med intervallets där <math> f(x) </math> är definierad. | ||
| − | + | På matematiska säger man: Definitionsintervallet <math> \; -2 < x < 2 \; </math> är <strong><span style="color:red">öppet</span></strong>, dvs ändarna tillhör inte intervallet. | |
Hade <math> f(x) </math> däremot varit definierad t.ex. i det "slutna" intervallet<span style="color:black">:</span> <math> -2 \leq x \leq 2 \;\; </math> hade <math> \; f(2) \, = \, f(-2) \, = \, 4 \; </math> varit funktionens globala maximum. | Hade <math> f(x) </math> däremot varit definierad t.ex. i det "slutna" intervallet<span style="color:black">:</span> <math> -2 \leq x \leq 2 \;\; </math> hade <math> \; f(2) \, = \, f(-2) \, = \, 4 \; </math> varit funktionens globala maximum. | ||
I praktiken behöver man inte leta efter globala extrema i definitionsintervallets ändpunkter om funktionen är definierad i ett öppet intervall. | I praktiken behöver man inte leta efter globala extrema i definitionsintervallets ändpunkter om funktionen är definierad i ett öppet intervall. | ||
| + | </div> <!-- tolv3 --> | ||
| − | == Exempel på en fullständig kurvkonstruktion == | + | <div class="exempel"> |
| − | + | == <b><span style="color:#931136">Exempel på en fullständig kurvkonstruktion</span></b> == | |
| + | <big> | ||
Funktionen<span style="color:black">:</span> | Funktionen<span style="color:black">:</span> | ||
| Rad 135: | Rad 147: | ||
d) Kontrollera dina resultat genom att rita grafen till <math> \, f(x) \, </math> med grafräknaren. | d) Kontrollera dina resultat genom att rita grafen till <math> \, f(x) \, </math> med grafräknaren. | ||
| − | ---- | + | </big> |
| + | </div> <!-- exempel --> | ||
| + | |||
| − | + | '''Lösning: a)''' | |
'''Steg 1''' Derivera <math> \, f(x) \, </math> två gånger: | '''Steg 1''' Derivera <math> \, f(x) \, </math> två gånger: | ||
| Rad 190: | Rad 204: | ||
| − | b) Beräkna funktionsvärdena i definitionsintervallets ändpunkter <math> \, 1 \, </math> och <math> \, 7 </math> och jämför dem med de lokala extrempunkternas <math> y</math>-koordinater<span style="color:black">:</span> | + | '''b)''' Beräkna funktionsvärdena i definitionsintervallets ändpunkter <math> \, 1 \, </math> och <math> \, 7 </math> och jämför dem med de lokala extrempunkternas <math> y</math>-koordinater<span style="color:black">:</span> |
:::<math> f(x) \, = \, x^3 - 12\,x^2 + 45\,x - 44 </math> | :::<math> f(x) \, = \, x^3 - 12\,x^2 + 45\,x - 44 </math> | ||
| Rad 210: | Rad 224: | ||
| − | c) Information från a) om lokala och från b) om globala extrema ger följande skisser: | + | '''c)''' Information från a) om lokala och från b) om globala extrema ger följande skisser: |
:[[Image: Fullstandig_kurvkonstruktion_1_80.jpg]] | :[[Image: Fullstandig_kurvkonstruktion_1_80.jpg]] | ||
| Rad 222: | Rad 236: | ||
| − | d) Grafräknaren ger: | + | '''d)''' Grafräknaren ger: |
:[[Image: Fullstandig_kurvkonstruktion_3_80.jpg]] | :[[Image: Fullstandig_kurvkonstruktion_3_80.jpg]] | ||
| Rad 233: | Rad 247: | ||
| − | [[Matte:Copyrights|Copyright]] © 2011-2015 | + | [[Matte:Copyrights|Copyright]] © 2011-2015 Math Online Sweden AB. All Rights Reserved. |
Versionen från 3 juli 2015 kl. 14.51
| <-- Förra avsnitt | Genomgång | Övningar | --> Nästa avsnitt |
Fortfarande förutsätts att alla funktioner \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) vi behandlar här är kontinuerliga i alla punkter av det betraktade området.
Översikt över punkter som kan identifieras med derivator \(-\) en sammanfattning av de två förra avsnitten
Fil:Oversikt Punkter 62 Ph.jpg
Med Min och Max i översikten ovan menas lokal minimi- och maximipunkt.
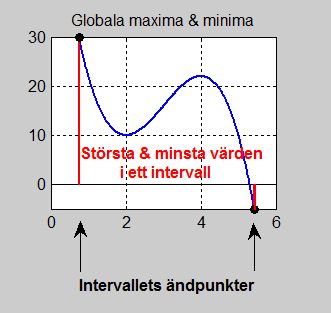
Största och minsta värden: globala maxima och minima
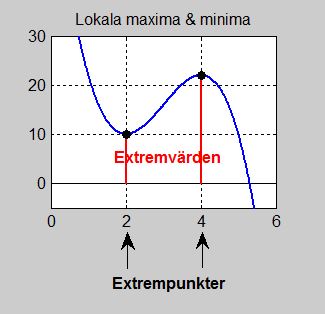
I avsnittet om Lokala maxima och minima hade vi tittat på sådana punkter som hade maximala och minimala \( \, y\)-värden i sin närmaste omgivning, därför "lokala", se bilden till höger.
I detta avsnitt ska vi betrakta sådana punkter som har största och minsta \( \, y\)-värden i ett intervall, därför "globala", se bilden till vänster.
 |
Globala maxima och minima är en funktions största och minsta värden
globalt dvs i ett intervall, närmare bestämt: Med globala maxima och globala minima menas punkter som har största resp. minsta \( \, y\)-värden i funktionens hela definitionsområde. På bilden till vänster visas de med • . Funktionens största värde är \( \, 30 \, \) och dess minsta värde är \( \, -5 \, \) (OBS! \( \, y\)-värden).
minima eller i intervallets ändpunkter.
att de ev. är identiska med funktionens lokala extrema. I ett mindre intervall blir exemplets lokala extrema, även globala. |
 |
I praktiken hittar man en funktions globala extrema genom att:
- Hitta funktionens lokala extrema med någon av de regler vi lärde oss i förra avsnitt (andraderivatan eller teckenstudium).
- Beräkna de lokala extremvärdena.
- Beräkna funktionsvärdena i definitionsintervallets ändpunkter.
- Jämföra de lokala extremvärdena med värdena i definitionsintervallets ändpunkter.
När saknas globalt extremum?
En funktion behöver inte nödvändigtvis ha extrema, varken lokala eller globala.
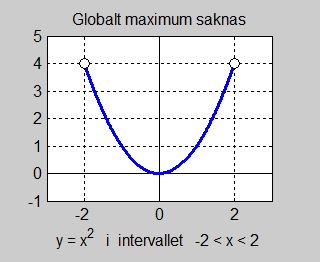
Detta kan hända när man letar efter globala extrema där man förväntar dem, t.ex. i definitionsintervallets ändpunkter. Det ser ut så \(-\) t.ex. i grafen \(-\) som om funktionen antog sina största (eller minsta) värden i intervallets ändpunkter. Att det inte behöver vara så visar följande exempel:
|
Exempel: Följande funktion är definierad i det angivna intervallet: \( y \, = \, f(x) \, = \, x^2 \quad \) Definitionsmängden: \( \quad -2 < x < 2 \) Av någon anledning är intervallets ändpunkter inte inkluderade i definitionsmängden. Dvs \( f(x) \) är inte definierad för \( \, x = 2 \), inte heller för \( \, x = -2 \). Grafen till höger visar detta genom de ihåliga ringarna i kurvans ändpunkter. \( f(x) \) har i \( x = 0 \) ett lokalt minimum som är även funktionens globala minimum. Däremot kan man inte ange något globalt maximum för \( f(x) \), av följande skäl: Om man t.ex. påstår att \( f(1,99) \) är funktionens största värde, är \( f(1,999) \) ännu större. Om man påstår att \( f(1,999) \) är största värdet, är \( f(1,9999) \) ännu större osv. Denna process har ingen ända och gäller även för \( f(-1,99\ldots) \). Varken \( f(2) \) eller \( f(-2) \) kan vara globala maxima, för båda är inte definierade. Slutligen kan man inte hitta något största värde:Globalt maximum saknas.
|
 |
Att globalt maximum saknas har inte med funktionens egenskaper att göra utan snarare med intervallets där \( f(x) \) är definierad.
På matematiska säger man: Definitionsintervallet \( \; -2 < x < 2 \; \) är öppet, dvs ändarna tillhör inte intervallet.
Hade \( f(x) \) däremot varit definierad t.ex. i det "slutna" intervallet: \( -2 \leq x \leq 2 \;\; \) hade \( \; f(2) \, = \, f(-2) \, = \, 4 \; \) varit funktionens globala maximum.
I praktiken behöver man inte leta efter globala extrema i definitionsintervallets ändpunkter om funktionen är definierad i ett öppet intervall.
Exempel på en fullständig kurvkonstruktion
Funktionen:
\( f(x) \, = \, x^3 \, - \, 12\,x^2 \, + \, 45\,x \, - \, 44 \qquad \) är definierad i intervallet \( \qquad 1 \leq x \leq 7 \)
a) Undersök algebraiskt om \( \,f(x) \, \) har några lokala maximi-, minimi- eller terasspunkter. Om ja, ange deras koordinater.
b) Bestäm funktionens största och minsta värden i definitionsintervallet.
c) Skissa för hand det ungefärliga förloppet till \( \, f(x) \, \) utgående från information från a) och b).
d) Kontrollera dina resultat genom att rita grafen till \( \, f(x) \, \) med grafräknaren.
Lösning: a)
Steg 1 Derivera \( \, f(x) \, \) två gånger:
- \[\begin{array}{rcl} f(x) & = & x^3 - 12\,x^2 + 45\,x - 44 \\ f'(x) & = & 3\,x^2 - 24\,x + 45 \\ f''(x) & = & 6\,x - 24 \end{array}\]
Steg 2 Sätt derivatan till \( \, 0 \):
- \[\begin{array}{rcl} 3\,x^2 - 24\,x + 45 & = & 0 \end{array}\]
Steg 3 Lös ekvationen som uppstår (beräkna derivatans nollställen):
- \[\begin{array}{rcl} 3\,x^2 - 24\,x + 45 & = & 0 \\ x^2 - 8\,x + 15 & = & 0 \\ \end{array}\]
- \[ \begin{array}{rcl} {\rm Vieta:} \quad x_1 \cdot x_2 & = & 15 \\ x_1 + x_2 & = & -(-8) = 8 \\ &\Downarrow& \\ x_1 & = & 3 \\ x_2 & = & 5 \end{array}\]
- Dessa är \( x\)-koordinater till eventuella lokala maximi-, minimi- eller terasspunkter.
Steg 4 Sätt in derivatans nollställen i andraderivatan:
\( {\color{White} x} \qquad \underline{x_1 = 3} \, \):
- \[ f''(x) \, = \, 6\,x - 24 \]
- \[ f''(3) \, = \, 6\cdot 3 - 24 = -6 < 0 \quad \Longrightarrow \quad x_1 = 3 \quad {\rm lokalt\;maximum.} \]
\( {\color{White} x} \qquad \underline{x_2 = 5} \, \):
- \[ f''(5) \, = \, 6\cdot 5 - 24 = 6 > 0 \quad \Longrightarrow \quad x_2 = 5 \quad {\rm lokalt\;minimum.} \]
- \[ f''(3) \neq 0 \quad {\rm och} \quad f''(5) \neq 0 \quad \Longrightarrow \quad f(x) \, {\rm har\;inga\;terasspunkter.} \]
Steg 5 Beräkna de lokala extrempunkternas \( y\)-koordinater:
- \[ f(x) \, = \, x^3 - 12\,x^2 + 45\,x - 44 \]
- \[ f(3) \, = \, 3^3 - 12\cdot 3^2 + 45\cdot 3 - 44 = 10 \quad \Longrightarrow \quad (3, 10) \quad {\rm är\;lokal\;maximipunkt.} \]
- \[ f(5) \, = \, 5^3 - 12\cdot 5^2 + 45\cdot 5 - 44 = 6 \quad \Longrightarrow \quad (5, 6) \quad {\rm är\;lokal\;minimipunkt.} \]
b) Beräkna funktionsvärdena i definitionsintervallets ändpunkter \( \, 1 \, \) och \( \, 7 \) och jämför dem med de lokala extrempunkternas \( y\)-koordinater:
- \[ f(x) \, = \, x^3 - 12\,x^2 + 45\,x - 44 \]
- \[ f(1) \, = \, 1^3 - 12\cdot 1^2 + 45\cdot 1 - 44 = -10 \]
- \[ f(7) \, = \, 7^3 - 12\cdot 7^2 + 45\cdot 7 - 44 = 26 \]
- Lokala minimivärdet var \( \, 6 \, \), se a).
- \[ -10 \, < \, 6 \quad \Longrightarrow \quad -10 \quad {\rm är\;funktionens\;minsta\;värde.} \]
- Lokala maximivärdet var \( \, 10 \, \), se a).
- \[ 26 \, > \, 10 \quad \Longrightarrow \quad 26 \quad {\rm är\;funktionens\;största\;värde.} \]
- De globala extremvärdena \( \, -10 \, \) och \( \, 26 \) antas av funktionen i definitionsintervallets ändpunkter därför att intervallet \( \, 1 \leq x \leq 7 \, \) är slutet.
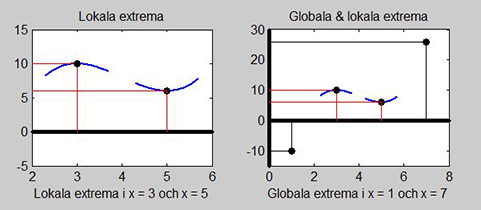
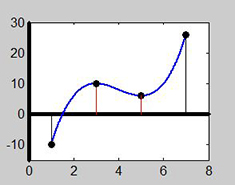
c) Information från a) om lokala och från b) om globala extrema ger följande skisser:
- Förutsätts kontinuitet hos \( \, f(x) -\) vilket vi kan göra pga att \( f(x) \) är en polynomfunktion \(-\) kan vi förbinda kurvsnuttarna från den högra bilden till följande kontinuerlig skiss:
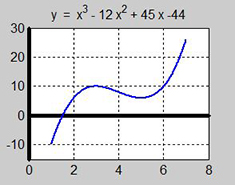
d) Grafräknaren ger:
Copyright © 2011-2015 Math Online Sweden AB. All Rights Reserved.
