Skillnad mellan versioner av "2.2 Genomsnittlig förändringshastighet"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 70: | Rad 70: | ||
::::<math> {\Delta y \over \Delta x} = {y\, {\rm:s\;ändring} \over x\, {\rm:s\;ändring}} \; = \; {f(2) \, - \, f(0) \over 2 - 0} \; = \; {2^2 \, - \, 0^2 \over 2 - 0} \; = \; {4 \, - \, 0 \over 2} \; = \; {4 \over 2} \; = \; {\color{Red} 2} </math> | ::::<math> {\Delta y \over \Delta x} = {y\, {\rm:s\;ändring} \over x\, {\rm:s\;ändring}} \; = \; {f(2) \, - \, f(0) \over 2 - 0} \; = \; {2^2 \, - \, 0^2 \over 2 - 0} \; = \; {4 \, - \, 0 \over 2} \; = \; {4 \over 2} \; = \; {\color{Red} 2} </math> | ||
| − | I intervallet <math> \, 0 \leq x \leq 2 </math> | + | I intervallet <math> \, 0 \leq x \leq 2 </math> växer funktionen <math> y = x^2 \, </math> med <math> \, {\color{Red} 2} \; y </math>-enheter per <math> \, x</math>-enhet. |
| − | + | ||
| − | + | ||
| + | Detta innebär att funktionens genomsnittliga förändringshastighet i intervallet är <math> \, {\color{Red} 2} </math>. | ||
| + | </div> <!-- exempel2 --> | ||
</td> | </td> | ||
<td> [[Image: Ex1a.jpg]]</td> | <td> [[Image: Ex1a.jpg]]</td> | ||
| Rad 79: | Rad 79: | ||
</table> | </table> | ||
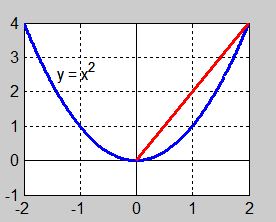
| − | + | I intervallet <math> \, 0 \leq x \leq 2 </math> ersätts kurvan <math> \, y = x^2 \, </math> av en <strong><span style="color:red">rät linje</span></strong> som kallas för kurvans <strong><span style="color:red">sekant</span></strong>. | |
| − | + | Sekantens <strong><span style="color:red">lutning</span></strong> är kurvans <strong><span style="color:red">genomsnittliga förändringshastighet</span></strong> i det betraktade <math> \,x</math>-intervallet. | |
| − | </ | + | |
Versionen från 10 oktober 2015 kl. 15.12
| <-- Förra avsnitt | Genomgång | Övningar | Nästa avsnitt --> |
Lektion 17: Genomsnittlig förändringshastighet
Exempel 1 Marginalskatt
Martins månadslön höjs från \( \, 23\;000 \, \) kr till \( \, 24\;200 \, \) kr.
I Skatteverkets skattetabell för 2015 (tabell 29, kolumn 2) hittar vi \( \, 5\;297 \, \) kr skatt för den gamla och \( \, 5\;676 \, \) kr skatt för den nya lönen.
Beräkna skattens genomsnittliga förändringshastighet som kallas för marginalskatt .
Lösning:
Skatten ökar med lönen. Den är beroende av lönen. Dvs skatten är en funktion av lönen.
Med följande beteckningar blir skatten \( \, y \, \) en diskret funktion av lönen \( \, x\, \) som är definierad i tabellform:
| \( \qquad\quad x \, = \, {\rm Månadslönen\;i\;kr} \)
\( \qquad\quad y \, = \, {\rm Skatten\;i\;kr} \) |
\( \qquad\qquad \) |
|
Förhållandet (kvoten) mellan skattehöjning och lönehöjning kallas för marginalskatt:
- \[ {\Delta y \over \Delta x} = {y\, {\rm:s\;ändring} \over x\, {\rm:s\;ändring}} = {{\rm Skattehöjningen} \over {\rm Lönehöjningen}} = {5\,676 - 5\,297 \over 24\,200 - 23\,000} \; = \; {379 \over 1200} \; = \; {\color{Red} {0,316}} \; = \; 31,6 \, \%\]
Man säger: marginalskatten är \( \, 31,6 \, \% \), vilket i ekonomiska termer betyder att Martin måste betala \(31,6\,\) öre i skatt för varje mer intjänad krona.
I matematiska termer har vi beräknat funktionen \( \, y\):s genomsnittliga förändringshastighet i det betraktade \( \, x\)-intervallet \(-\) vilket ger marginalskatten.
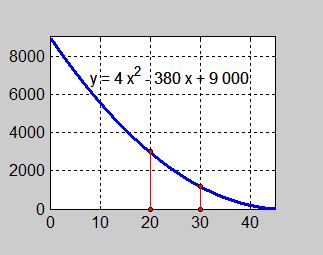
Vi ersätter nu den diskreta skattefunktionen i tabellform med en kontinuerlig funktion som är given med ett uttryck:
Exempel 2 Kvadratisk funktion
Givet: Funktionen \( \, y \, = \, f(x) \, = \, x^2 \)
Sökt: Funktionens genomsnittliga förändringshastighet i intervallet \( \, 0 \leq x \leq 2 \). Lösning:
I intervallet \( \, 0 \leq x \leq 2 \) växer funktionen \( y = x^2 \, \) med \( \, {\color{Red} 2} \; y \)-enheter per \( \, x\)-enhet. Detta innebär att funktionens genomsnittliga förändringshastighet i intervallet är \( \, {\color{Red} 2} \). </div> |
<td>