Skillnad mellan versioner av "2.4 Derivatans definition"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 80: | Rad 80: | ||
| − | Tidigare [[2.2_Genomsnittlig_förändringshastighet#Exempel_3_Oljetank|<strong><span style="color:blue">(Exempel 3 d)</span></strong>]] hade vi fått | + | Tidigare [[2.2_Genomsnittlig_förändringshastighet#Exempel_3_Oljetank|<strong><span style="color:blue">(Exempel 3 d)</span></strong>]] hade vi fått <math> -\,379,6\, </math> för den genomsnittliga utströmningshastighet i intervallet <math> 0 \,\leq\, x \,\leq\, 0,1 </math>, vilket är ett närmevärde för derivatan, som nu visar sig vara ganska bra. Närmevärdet hade blivit ännu precisare om vi hade valt t.ex. intervallet <math> 0 \,\leq\, x \,\leq\, 0,01 </math> eller <math> 0 \,\leq\, x \,\leq\, 0,001 </math> osv. Det exakta värdet <math> -\,380 \, </math> får man om man i intervallet <math> 0 \,\leq\, x \,\leq\, h </math> låter <math> h \to 0 </math>. |
I exemplet ovan är oljans momentana utströmningshastighet derivatans <strong><span style="color:red">fysikaliska tolkning</span></strong>. | I exemplet ovan är oljans momentana utströmningshastighet derivatans <strong><span style="color:red">fysikaliska tolkning</span></strong>. | ||
Versionen från 9 november 2015 kl. 10.12
| <-- Förra avsnitt | Genomgång | Övningar | Nästa avsnitt --> |
Lektion 18 Derivatans definition
Derivatan i en punkt
Exempel Oljetank
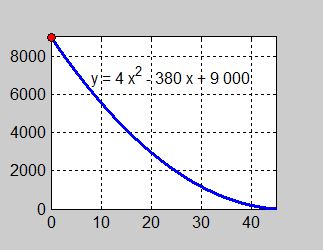
| En oljetank läcker genom ett hål i tankens botten (Exempel 3 i förra avsnitt).
Oljans utströmning beskrivs av funktionen:
där \( \quad\; x \, = \, {\rm Tiden\;i\;minuter} \)
a) Beräkna oljans genomsnittliga utströmningshastighet i intervallet \( \, 0 \,\leq\, x \,\leq\, h \quad \) \( \;\;\, \) som ett uttryck i \( \, h > 0 \, \) (något positivt tal). b) Beräkna oljans momentana utströmningshastighet i punkten \( \, x = 0 \) genom att \( \;\;\, \) i uttrycket från a) låta \( \, h \, \) gå mot \( \, 0 \). |
 |
Lösning:
a) Den allmänna definitionen till genomsnittlig förändringshastighet är:
- \[ {\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h} \qquad {\rm i\;\;intervallet } \qquad x_1 \,\leq\, x \,\leq\, x_1 + h \]
I exemplet Oljetank är \( \,x_1 = 0 \). Då har vi:
- \[ {\Delta y \over \Delta x} \; = \; {f(0 + h) \, - \, f(0) \over h} \; = \; {f(h) \, - \, f(0) \over h} \qquad {\rm i\;\;intervallet } \qquad 0 \,\leq\, x \,\leq\, h \]
För \( \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, \) får vi \( \, f\,(h) \, = \, 4\,h^2 - 380\,h + 9\,000 \, \) och \( \, f\,(0) \, = \, 9\,000 \).
Då blir oljans genomsnittliga utströmningshastighet i intervallet \( 0 \,\leq\, x \,\leq\, h \, \):
- \[ {\Delta y \over \Delta x} \,=\, {f(h) \, - \, f(0) \over h} \,=\, {4\,h^2 - 380\,h + 9\,000 \,-\, 9\,000 \over h} \,=\, {4\,h^2 - 380\,h \over h} \,=\, {{\color{Red} h}\,(4\,h - 380) \over {\color{Red} h}} \,=\, 4\,h - 380 \]
b) Nu låter vi i uttrycket \( 4\,h - 380 \) för den genomsnittliga utströmningshastigheten \( \, h\, \) gå mot \( 0\, \) för att få oljans momentana utströmningshastighet i \( \, x = 0\, \).
Dvs vi beräknar gränsvärdet:
- \[ \qquad \displaystyle \lim_{h \to 0}\, {(4\,h - 380)} \,=\, -\,380 \]
\( -\,380\, \) är oljans momentana utströmningshastighet i \( \, x = 0 \, \). Dvs vid denna tidpunkt sjunker oljan med exakt \( 380\, \) liter per minut.
Ett annat ord för den momentana utströmningshastigheten är derivatan. Vi fick den genom att först (a) ställa upp den genomsnittliga förändringshastigheten i intervallet \( \, 0 \,\leq\, x \,\leq\, h \, \) som ett uttryck i \( \, h \, \) och sedan (b) beräkna uttryckets gränsvärde för \( \, h \to 0 \). Resultatet kan sammanfattas så här:
Funktionen \( \, f\,(x) \, \) har i punkten \( \, x = 0 \, \) derivatan \( \quad f\,{\color{Red} '}\,(0) \,=\, -\,380 \quad \).
\( f\,{\color{Red} '}\,(0) \;\; {\rm läses\;så\;här:\;" } f \; {\rm {\color{Red} {prim}}\;av\; } 0 \; {\rm " }. \)
Tidigare (Exempel 3 d) hade vi fått \( -\,379,6\, \) för den genomsnittliga utströmningshastighet i intervallet \( 0 \,\leq\, x \,\leq\, 0,1 \), vilket är ett närmevärde för derivatan, som nu visar sig vara ganska bra. Närmevärdet hade blivit ännu precisare om vi hade valt t.ex. intervallet \( 0 \,\leq\, x \,\leq\, 0,01 \) eller \( 0 \,\leq\, x \,\leq\, 0,001 \) osv. Det exakta värdet \( -\,380 \, \) får man om man i intervallet \( 0 \,\leq\, x \,\leq\, h \) låter \( h \to 0 \).
I exemplet ovan är oljans momentana utströmningshastighet derivatans fysikaliska tolkning.
Men derivatan har även en intuitiv geometrisk tolkning:
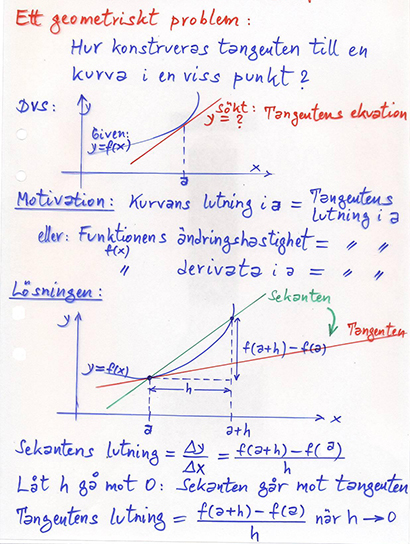
Från sekanten till tangenten
Vi ställer frågan efter kurvan \( \, y = f\,(x)\):s lutning i en given punkt \( \, x = a \, \), som är identisk med tangentens lutning i denna punkt. Med denna lutning samt punkten kan vi ställa upp tangentens ekvation.
Tangentens lutning får vi genom att först beräkna sekantens lutning och sedan låta sekanten gå över till tangenten.
Derivatan som ett gränsvärde (ett tal)
Derivatan som funktion
Både det fysikaliska Exemplet Oljetank och den geometriska tolkningen Från sekanten till tangenten definierar derivatan lokalt som ett värde dvs ett tal.
Men hur blir det om punkten \( \, a \) på \( \, x\)-axeln inte längre är konstant utan variabel? I så fall borde man tillämpa den lokala definitionen av derivatan på varenda punkt \( \, a \) och på så sätt få en massa värden för derivatan i varenda punkt \( \, a \). Tänker man sig att alla dessa derivatvärden är tilldelade sina respektive \( \, x\)-värden, bildar denna tilldelning en ny funktion som är den ursprungliga funktionens derivata, fast inte längre som ett tal utan som ett funktionsuttryck. På så sätt har vi fått derivatan som en funktion.
Låt oss verifiera detta genom att vidareutveckla vårt sista exempel ovan \( y = f\,(x) = 5\,x^2 \). Nu ska vi inte längre beräkna \( f\,'\,(4)\) utan ställa upp den nya funktionen \( y\,' = f\,'\,(x) \) dvs funktionen \( f\,(x) = 5\,x^2\):s derivata:
En annan notation för derivatan av en funktion \( y = f(x)\, \) som anknyter till \( \displaystyle {\Delta y \over \Delta x} \), är \( \displaystyle {dy \over dx} \) vilket vi dock inte kommer att använda så ofta.
Allmän definition
Slutligen kan vi sammanfatta:
\( \displaystyle f\,'\,(x) \; = \; \lim_{h \to 0}\,\,{f(x + h) \, - \, f(x) \over h} \quad {\rm är\;funktionen } \; y = f\,(x){\rm :s \;\, {\color{Red} {derivata}}\;.} \)
- \( {\color{White} x} f\,'\,(x) \;\; {\rm läses\;" } f \; {\rm prim\;av\; } x \; {\rm " }. \)
Exempel Oljetank (utvidgat)
En oljetank läcker genom ett hål i tankens botten. Utströmningen av oljan beskrivs av funktionen:
- \[ y \, = \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \]
Ställ upp utströmningsfunktionens derivata med hjälp av derivatans definition. Rita grafen till den nya funktionen.
Lösning:
Först ställer vi upp de uttryck som ingår i derivatans definition och förenklar dem:
\[ \begin{array}{lcl} f(x + h) & = & 4\,(x+h)^2 - 380\,(x+h) + 9\,000 = 4\,(x^2 + 2\,x\,h + h^2) - 380\,x - 380\,h + 9\,000 = \\ & = & 4\,x^2 + 8\,x\,h + 4\,h^2 - 380\,x - 380\,h + 9\,000 \\ f(x + h) - f(x) & = & 4\,x^2 + 8\,x\,h + 4\,h^2 - 380\,x - 380\,h + 9\,000 - (4\,x^2 - 380\,x + 9\,000) = \\ & = & 4\,x^2 + 8\,x\,h + 4\,h^2 - 380\,x - 380\,h + 9\,000 - 4\,x^2 + 380\,x - 9\,000 \;\;\, =\\ & = & 8\,x\,h + 4\,h^2 - 380\,h \, = \, h\,(8\,x + 4\,h - 380) \\ {f(x + h) - f(x) \over h} & = & {h\,(8\,x + 4\,h - 380) \over h} \, = \, 8\,x + 4\,h - 380 \end{array}\]
| Nu sätter vi in det förenklade uttrycket ovan i derivatans definition och beräknar gränsvärdet:
\[ f\,'\,(x) \; = \; \lim_{h \to 0}\,\,{f(x + h) \, - \, f(x) \over h} \,=\, \lim_{h \to 0}\,{(8\,x + 4\,h - 380)} \,=\, 8\,x - 380 \] \( f\,'\,(x) = 8\,x - 380 \) är derivatan till oljans utströmningsfunktion \( y = f\,(x) \).
Att derivatan är en linjär funktion och dess graf en rät linje är ingen tillfällighet utan ett exempel på regeln: Derivatan av andragradsfunktioner är linjära.
|
Fil:Oljetank derivata.jpg |
Ett annat exempel på denna regel hade vi sett när vi i kapitlets inledande Aktivitet (Lösning, punkt 6) approximerade derivatan och ritade grafen till hastighetsfunktionen till Yulias hopp från 10 m-torn.
I efterhand kan vi nu verifiera det i Exempel Oljetank beräknade värdet av \( f\,(x)\):s derivata i punkten \( \, x = 0 \) genom att sätta in \( \, x = 0 \) i derivatans funktion \( f\,'\,(x) = 8\,x - 380 \):
- \[ f\,'\,(0) \,=\, 8 \cdot 0 - 380 \,=\, 0 - 380 \,=\, -\,380 \]
Vid tiden \( x = 0\, \) sjönk oljan med \( 380\, \) liter per minut som var den största utströmningshastigheten när oljan hade mest volym och utövade det största trycket på hålet.
Internetlänkar
http://www.youtube.com/watch?v=OyKmc2bPWe0
http://www.youtube.com/watch?v=8of_svLfcjk
http://www.youtube.com/watch?v=OY8CeLUxE64&feature=related
http://www.youtube.com/watch?v=2wH-g60EJ18&feature=related
http://www.larcentrum.org/Safir/MA1203W/htm/m03_deriv1/m03_deriv_definition.htm
http://www.naturvetenskap.org/index.php?option=com_content&view=article&id=129&Itemid=132
Copyright © 2011-2015 Taifun Alishenas. All Rights Reserved.