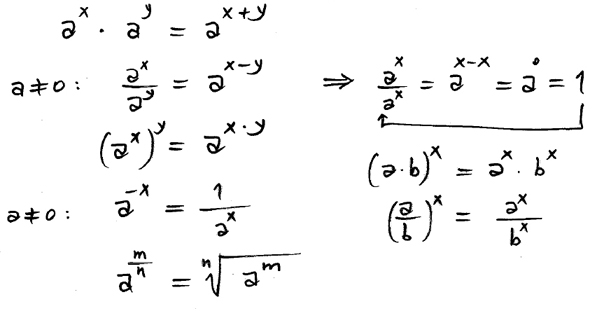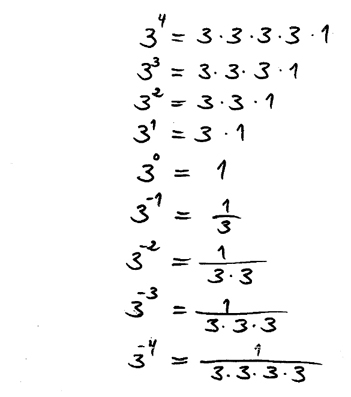Skillnad mellan versioner av "1.5 Potenslagarna"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 17: | Rad 17: | ||
Potenslagarna ovan gäller även för exponenter <math> x\, </math> som är negativa eller bråktal, även om vi inledningsvis definierade potensen <math> a^x\, </math> endast för positiva heltal <math> x\, </math>. | Potenslagarna ovan gäller även för exponenter <math> x\, </math> som är negativa eller bråktal, även om vi inledningsvis definierade potensen <math> a^x\, </math> endast för positiva heltal <math> x\, </math>. | ||
| − | '''Påstående''': | + | '''Påstående (Nollte potens)''': |
| + | |||
| + | :::::<math> a^0 \; = \; 1 </math> | ||
| + | |||
| + | '''Bevis''': | ||
| + | |||
| + | Påståendet kan bevisas genom att använda potenslagen för division av potenser med samma bas: | ||
| + | |||
| + | :::::<math> a^0 \; = \; a^{x-x} \; = \; {a^x \over a^x} \; = \; 1 </math> | ||
| + | |||
| + | '''Påstående (Negativ exponent)''': | ||
:::::<math> a^{-x} \; = \; {1 \over a^x} </math> | :::::<math> a^{-x} \; = \; {1 \over a^x} </math> | ||
| Rad 23: | Rad 33: | ||
'''Bevis''': | '''Bevis''': | ||
| − | Påståendet kan bevisas | + | Påståendet kan bevisas genom att använda potenslagen för division av potenser med samma bas samt lagen om nollte potensen: |
:::::<math> a^{-x} \; = \; a^{0-x} \; = \; {a^0 \over a^x} \; = \; {1 \over a^x} </math> | :::::<math> a^{-x} \; = \; a^{0-x} \; = \; {a^0 \over a^x} \; = \; {1 \over a^x} </math> | ||
Versionen från 6 mars 2011 kl. 14.25
Ett uttryck av formen \( a^x\, \) kallas potens. \( a\, \) heter basen och \( x\, \) exponenten.
Om \( x\, \) är ett positivt heltal kan \( a^x\, \) definieras som en förkortning för upprepad multiplikation av a:
- \[ a^x = \underbrace{a \cdot a \cdot a \cdot \quad \ \cdots \quad \cdot a}_{x} \]
Dvs a multiplicerat med sig själv x gånger. T.ex.:
- \[ a^2 = a \cdot a \]
- \[ a^3 = a \cdot a \cdot a \]
Följande lagar gäller för potenser:
Potenslagarna ovan gäller även för exponenter \( x\, \) som är negativa eller bråktal, även om vi inledningsvis definierade potensen \( a^x\, \) endast för positiva heltal \( x\, \).
Påstående (Nollte potens):
- \[ a^0 \; = \; 1 \]
Bevis:
Påståendet kan bevisas genom att använda potenslagen för division av potenser med samma bas:
- \[ a^0 \; = \; a^{x-x} \; = \; {a^x \over a^x} \; = \; 1 \]
Påstående (Negativ exponent):
- \[ a^{-x} \; = \; {1 \over a^x} \]
Bevis:
Påståendet kan bevisas genom att använda potenslagen för division av potenser med samma bas samt lagen om nollte potensen:
- \[ a^{-x} \; = \; a^{0-x} \; = \; {a^0 \over a^x} \; = \; {1 \over a^x} \]