Skillnad mellan versioner av "Kapitel 4 Integraler"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 116: | Rad 116: | ||
En fallskärmshoppare faller fritt utan att öppna fallskärmen. | En fallskärmshoppare faller fritt utan att öppna fallskärmen. | ||
| − | Hastigheten | + | Hastigheten ökar enligt <math> \, v(t) = 80 \, (1 \, - \, 0,88\,^t) \, </math> där <math> \, t = \, </math> tiden i sek. |
Hur långt har hopparen fallit när <math> \, v = 40 \, </math> m/s? | Hur långt har hopparen fallit när <math> \, v = 40 \, </math> m/s? | ||
Versionen från 7 mars 2016 kl. 15.43
Utdrag ur planeringen:
4.1 Primitiva funktioner
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 175
| \( \quad \) | 
|
\( \qquad \) |
Integration är den inversa operationen till derivering. \( \quad \) Primitiv funktion = "Anti"derivata
Derivata Integral Fysikalisk tolkning: Hastighet Sträcka Geometrisk tolkning: Kurvans lutning Area under kurvan Matematisk tolkning: Limes av differenskvot Limes av oändlig summa
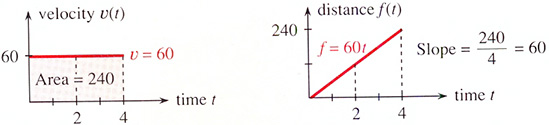
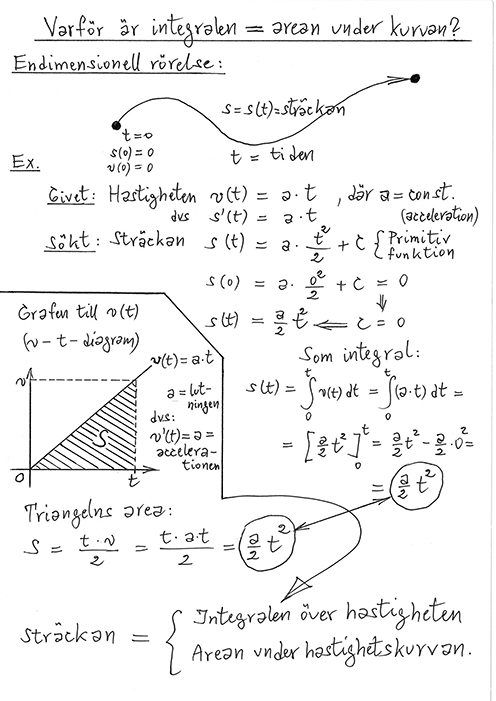
Ex. på "Area under kurvan" : \( \quad \) Rörelse med konstant hastighet 60 km/h
OBS! Area under kurvan är det inversa till kurvans lutning (eng. slope), när det gäller integration vs. derivering.
Sammanfattning: Givet: \( \quad f\,(x) \) Sökt: \( \quad \) Primitiv funktion \( \; F\,(x) \quad \) så att \( \quad F\,'\,(x) = f\,(x) \) |
Ex.: \( f\,(x) \; = \; x\,^3 + 5 \) \( F(x) = \frac{1}{4} x\,^4 + 5 x + C \, , \; C={\rm const.} \) |
\( \;\qquad\; C \; \) kallas för integrationskonstanten och bestäms av villkor (krav) som ställs på \( \, F(x) \, \). \( \quad {\bf {\color{Red} {\downarrow}}} \quad \)
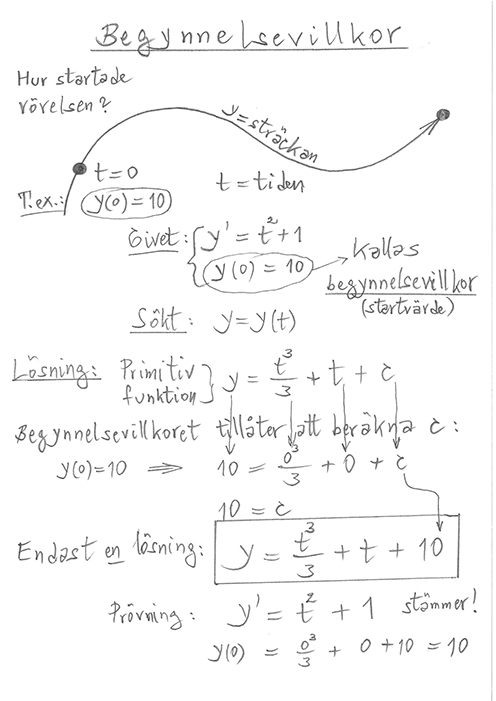
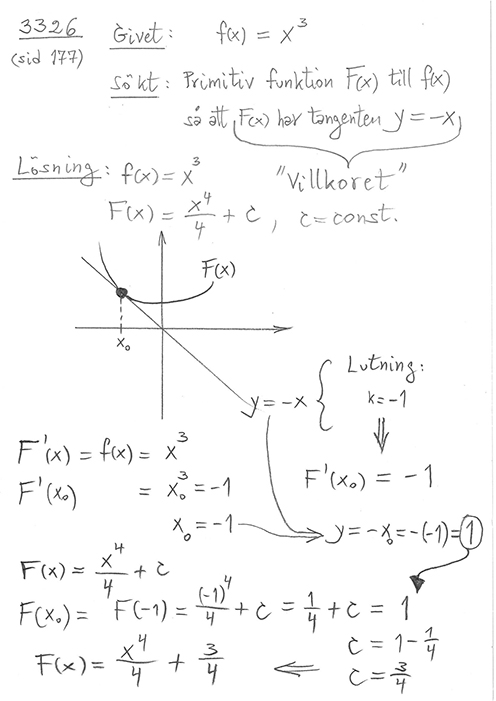
4.2 Primitiva funktioner med villkor
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 177
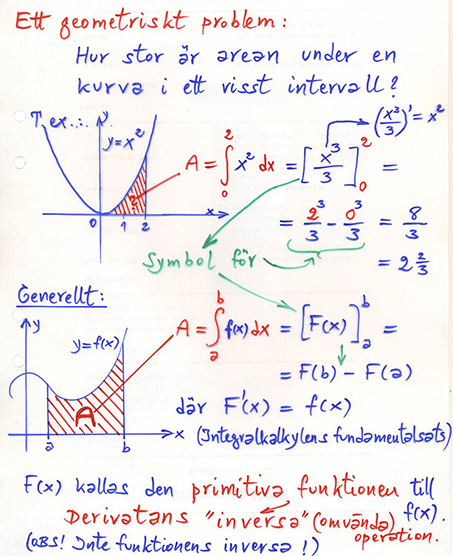
4.3 Integral som area under kurvan
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 180
4.4a Integral som Limes av oändlig summa
4.4b Integralberäkning med primitiv funktion
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 185
4.5 Användning av integraler
Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 188-90
3438 (3c-boken, sid 190):
En fallskärmshoppare faller fritt utan att öppna fallskärmen.
Hastigheten ökar enligt \( \, v(t) = 80 \, (1 \, - \, 0,88\,^t) \, \) där \( \, t = \, \) tiden i sek.
Hur långt har hopparen fallit när \( \, v = 40 \, \) m/s?
Copyright © 2011-2016 Math Online Sweden AB. All Rights Reserved.