Skillnad mellan versioner av "1.2 Faktorisering av polynom"

\[ {\rm {\color{Red} {OBS!\quad Vanlig\;fel\;åtgärd:}}} \quad\; (x-3) \cdot (x-4) \; = \; x^2 - 4\,x - 3\,x + 3 \cdot 4 \; = \; x^2 \, - \, 7\,x \, + \, 12 \; = \; 0 \]

\[ \qquad\quad\; {\rm Rätt\;åtgärd: \qquad\quad\; Räkna\;inte!\quad Tänk\;istället\;sä\;här:} \]

För att \( \, (x-3) \cdot (x-4) \, \) ska vara \( 0 \), måste antingen \( \, (x-3) \, \) eller \( \, (x-4) \, \) vara \( \, 0 \; \): \( \quad a \cdot b = 0 \;\; \Rightarrow \;\; a = 0 \; \) eller \( \; b = 0 \)

För att \( \, (x-3) \, \) eller \( \, (x-4) \, \) ska vara \( \, 0 \,\) måste \( \, x \, \) antingen vara \( \, 3 \, \) eller \( \, 4 \).

Alltså har ekvationen de två lösningarna:

\(\qquad\begin{align} x_1 & = 3 \\ x_2 & = 4 \end{align} \)

Nollproduktmetoden ger oss ekvationens lösningar utan att vi behöver räkna!

Den felaktiga åtgärden ovan är formellt matematiskt inte fel, men är ineffektiv och förstör faktorformen.

Faktorformen är den struktur som gör nollproduktmetoden och därmed den effektiva lösningen möjlig.

Ett polynom i faktorform visar sina nollställen istället för koefficienterna.

Men hur får man faktorformen om man har polynomet som en summa av termer? Man måste bestämma nollställena:

Faktorisering av 2:a gradspolynom (normalform)

Uppgiften: Faktorisera polynomet \( \, x^2 - 7\,x + 12 \).

Lösningen: Vi beräknar polynomets nollställen:

\[ x^2 - 7\,x + 12 = 0 \]

För att snabbt lösa denna 2:a gradsekvation som ett led i faktoriseringsprocessen

använder vi Vietas formler:

\[ \begin{align} x_1 + x_2 & = -p = -(-7) = 7 \\ x_1 \cdot x_2 & = \;\;\; q = 12 \end{align}\]

Dvs vi behöver hitta två tal vars produkt är \( \, 12 \, \) och vars summa är \( \, 7 \, \).

Med lite provande kommer man fram till:

\[\begin{align} x_1 & = 3 \\ x_2 & = 4 \end{align}\]

eftersom \( \, 3 + 4 = 7 \, \) och \( \, 3 \cdot 4 = 12 \). Därmed är polynomets faktorisering:

\[ x^2 - 7\,x + 12 \; = \; \underline{(x - 3) \, \cdot \, (x - 4)} \]

Självklart hade man kunnat använda även p-q-formeln för att lösa 2:a gradsekvationen. Då hade det sett ut så här:

\[\begin{array}{rcl} x^2 - 7\,x + 12 & = & 0 \\ x_{1,2} & = & 3,5 \pm \sqrt{12,25 - 12} \\ x_{1,2} & = & 3,5 \pm \sqrt{0,25} \\ x_{1,2} & = & 3,5 \pm 0,5 \\ x_1 & = & 3 \\ x_2 & = & 4 \end{array}\]

Man ser att Vieta inte bara är en enklare och snabbare metod än p-q-formeln utan även minimerar risken för felräkning.

Faktorformen (produkten) är resultat av faktorisering (processen). Exemplets polynom är av grad \( \, 2\), medan dess ingredienser dvs faktorerna \( \, (x-3) \, \) och \( \, (x-4) \, \) är polynom av grad \( \, 1\). Detta kan jämföras med faktoriseringen \( \, 12 \, = \, 3 \cdot 4 \), där faktorerna \( \, 3 \, \) och \( \, 4 \, \) är mindre än \( \, 12 \, \). Man har splittrat upp talet \( \, 12 \,\) i sina beståndsdelar \( \, 3 \, \) och \( \, 4 \), precis som man splittrar upp polynomet \( \, x^2 - 7\,x + 12 \, \) i sina beståndsdelar \( \, (x-3)\, \) och \( \, (x-4) \).

Faktorisering är relevant av olika skäl: För det första tillåter faktorformen förkortning och därmed förenkling av komplexa algebraiska uttryck. För det andra avslöjar faktorformen polynomets nollställen.

Det vi genomförde för vårt exempel kan generaliseras till alla 2:gradspolynom, åtminstone sådana som är givna i normalform:

Sats:

Faktorisering med 2 nollställen

Om 2:a gradspolynomet \( x^2 + p\,x + q \) har nollställena \( x_1\, \) och \( x_2\, \) så gäller:

\[ x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) \]

För att bevisa satsen ovan kan man t.ex.

sätta in p-q-formeln för \( x_1\, \) och \( x_2\, \),
utveckla produkten på högerledet och
genomföra jämförelse av koefficienter.

Se beviset i lösningen till övning 13.

Det finns motsvarande satser om polynom av högre grad än 2, se Algebrans fundamentalsats.

Slutsats:

För att faktorisera ett 2:a gradspolynom måste vi beräkna dess nollställen \( x_1\, \) och \( x_2\, \).

Sedan blir faktoriseringen: \( \qquad (x-x_1) \cdot (x-x_2) \)

Rotens olika betydelser

Ordet rot har i matematiken olika betydelser i olika sammanhang:

Räkneoperationen rotdragning med rottecknet \( {\color{White}{y=}}\!\!\!\!\!\!\!\!\sqrt{\color{White}x} \) som symbol, t.ex. roten ur \( 4\, \) är \( 2\, \) osv.
Lösningen av en ekvation. Rot är synonym till en ekvations lösning. T.ex. är \( x_1 = 2\, \) och \( x_2 = -2\, \) rötter dvs lösningar till ekvationen \( x^2 = 4\, \).
Nollstället till ett polynom. Rot är synonym till ett polynoms nollställe. I exemplet ovan är \( x_1 = 2\, \) och \( x_2 = -2\, \) rötter dvs nollställen till polynomet \( x^2 - 4\, \).

Sammanhanget avgör vilken betydelse som gäller just i den aktuella kontexten.

Dubbelrot

När vi nu i fortsättningen pratar om en dubbelrot menar vi två lösningar till en ekvation som sammanfaller, vilket även kan uppfattas som endast en lösning.

Sats:

Faktorisering med 1 nollställe

Om 2:gradspolynomet \( x^2 + p\,x + q \) endast har ett nollställe \( x_1\, \) så gäller:

\[ x^2 + p\,x + q = (x-x_1)^2 \]

Ett sådant nollställe kallas för dubbelrot till ekvationen \( x^2 + p\,x + q = 0 \).

Exempel

Polynomet \( x^2 - 6\,x + 9 \) har dubbelroten \( x = 3\, \) eftersom \( x^2 - 6\,x + 9 \, = \, (x-3)\,^2 \), se exemplet från repetitionen om Vieta.

Vi ritar grafen till polynomfunktionen och undersöker på vilket sätt kurvan "skär" \( \, x\)-axeln.

Grafen till polynomfunktionen \( \; y = x^2 - 6\,x + 9 \; {\rm :} \quad\quad \)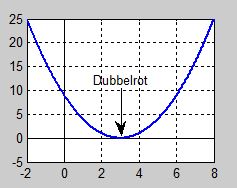

Grafen visar att kurvan inte skär utan bara berör \(\,x\)-axeln vid \( x = 3\, \). Dvs det finns endast en gemensam punkt mellan kurvan och \(\,x\)-axeln.

Dubbelrötter ligger på gränsen mellan att skära (två lösningar) och inte skära \(\,x\)-axeln (ingen lösning alls). Matematiskt uttrycker sig detta i faktoriseringens form:

\[ x^2 - 6\,x + 9 = (x-3) \cdot (x-3) = (x-3)\,^2 \]

Det intressanta med dubelrötter är att vi endast har en lösning \( x = 3\, \) till 2:a gradsekvationen \( x^2 - 6 x + 9 = 0\, \). Fast, om vi tittar på faktorformen \( (x - 3) \cdot (x - 3) = 0 \) kan man lika bra säga att vi har två identiska lösningar eller två som sammanfaller - ett filosofiskt dilemma som man matematiskt brukar lösa upp genom att kalla lösningen för en dubbelrot.

Andra viktiga egenskaper av dubbelrötter kommer vi att lära känna senare när vi i kapitel 2 behandlar derivering.

Internetlänkar

http://tutorial.math.lamar.edu/Classes/Alg/Factoring.aspx

http://mathworld.wolfram.com/PolynomialFactorization.html

http://www.mathsisfun.com/algebra/fundamental-theorem-algebra.html

http://www.sosmath.com/algebra/factor/fac04/fac04.html

http://www.lboro.ac.uk/research/helm/C_HELM_backup_24nov03/helm_website/documents/wb03_blk3.pdf

@@ Rad 156: / Rad 156: @@
 </big>
-<big><b><span style="color:#931136">Slutsats:</span></b></big></big>
+<big><big><b><span style="color:#931136">Slutsats:</span></b></big>
 <div class="ovnE">
 För att faktorisera ett 2:a gradspolynom måste vi beräkna dess nollställen <math> x_1\, </math> och <math> x_2\, </math>.
 Sedan blir faktoriseringen<span style="color:black">:</span> <math> \qquad (x-x_1) \cdot (x-x_2) </math>
-</div>
+</div></big>

Skillnad mellan versioner av "1.2 Faktorisering av polynom"

Versionen från 6 september 2017 kl. 21.17

Polynom i faktorform

Exempel

Nollproduktmetoden

Faktorisering av 2:a gradspolynom (normalform)

Faktorisering med 2 nollställen

Rotens olika betydelser

Dubbelrot

Faktorisering med 1 nollställe

Exempel

Internetlänkar

Navigeringsmeny

Personliga verktyg

Matematik 3c

Sök