Skillnad mellan versioner av "Repetition: 10-logaritmer"

Versionen från 15 september 2017 kl. 12.03

<< Förra avsnitt

Genomgång

Quiz

Övningar

Nästa avsnitt >>

Genomgång+

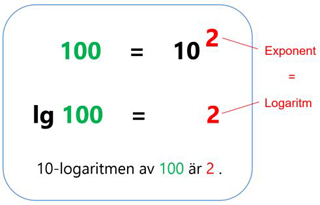
Logaritm = exponent

10-logaritm = exponent till basen \( 10 \).

\(\lg\) är symbolen för 10-logaritmen.

\(\lg 100 \, \) = tal som basen \(10\) ska upp-

höjas till, för att ge \(100\). Det talet är \({\color{Red} 2}\).

Generellt:

Definition:

\(\lg a \, \) = tal som basen \(10\) ska upphö-

\( \qquad\;\;\; \) jas till, för att ge \( \, a \, \).

Exempel på 10-logaritmer

\(\lg 125 \, \) = tal som basen \(10\) ska upp-

\( \qquad\quad\;\;\; \) höjas till, för att ge \(125\).

Räknaren: \( \boxed{\text{LOG}}\) \((125) = \) \( {\color{Red} {2,09691\ldots}} \)

Potensform: \( \;\;\; 125 \; = \; 10\,^{\color{Red} {2,09691\ldots}} \)

\( \qquad\qquad\qquad\quad\;\,\, \Updownarrow \)

Log-form: \( \;\; \lg\,125 \; \)\( \; = \; {\color{Red} {2,09691\ldots}} \)

\(\lg\,0,1\) = \(\lg\,(\frac{1}{10})\) = tal som basen \(10\)

ska upphöjas till, för att ge \(\frac{1}{10}\).

Potensform: \( \quad\;\;\; \frac{1}{10} \; = \; 10\,^{\color{Red} {-1}} \)

\( \qquad\qquad\qquad\qquad\, \Updownarrow \)

Log-form: \( \;\;\;\; \lg\,0,1 \; \)\( \; = \; {\color{Red} {-1}} \)

10-logaritmens definitionsmängd

\(\lg x \, \) är definierad endast för \( \, x>0 \, \).

För \( \, x \leq 0 \, \) är \( \, \lg x \, \) inte definierad.

Exempel:

\( \boxed{\text{LOG}}\) \(({\color{Red} {-1}}) \quad \rightarrow \quad {\color{Red} {\text{ERROR}}} \)

\( \boxed{\text{LOG}}\) \(({\color{Red} {\;0\;}}) \quad\, \rightarrow \quad {\color{Red} {\text{ERROR}}} \)

Inversegenskapen

\( \, y \, = \, \lg\,x \, \) är den inversa (motsatta)

funktionen till \( \, y \, = \, 10\,^x \, \), dvs:

\( \lg\,(10^{\,{\color{Red} x}}) = {\color{Red} x} \quad {\rm och\; } \quad 10^{\,\lg{\color{Red} x}} = {\color{Red} x} \)

\( \boxed{\text{LOG}} \, \) och \( \, 10 \) \( \boxed{\text{ ^ }} \, \) tar ut varandra.

Exempel:

\( \boxed{\text{LOG}}\) \(({\color{Red} {1,5}}) \quad = \quad \cdots\cdots \)

\( 10 \) \( \boxed{\text{ ^ }} \; \boxed{\text{ANS}}\) \( \;\;\; = \quad\;\, {\color{Red} {1,5}} \)

\( \;\; \boxed{\text{ANS}} \) är räknarens sist visade svar.

\( 10 \) \( \boxed{\text{ ^ }}\) \({\color{Red} {2,5}} \quad\;\;\, = \quad \) \( \cdots\cdots \)

\( \boxed{\text{LOG}} \, \left(\,\boxed{\text{ANS}}\,\right)\) \( = \quad\;\, {\color{Red} {2,5}} \)

Exponentialekvationer av typ \( \; 10\,^x \, = \, b \)

\(\begin{array}{rcll} 10^{\,x} & = & 68 & | \; \lg\,(\,\cdot\,) \\ {\color{Red} {\lg}}\,({\color{Red} {10}}^{\,x}) & = & \lg\,68 & \\ x & = & \lg\,68 & \\ x & = & 1,8325089\ldots & \\ \end{array}\)

Kontroll: \( \qquad 10^{\,1,832508913} \, = \, 68 \)

I rad 1 logaritmeras ekvationens båda led.

I rad 2➛3 ger inversegenskapen: \( {\color{Red} {\lg}}({\color{Red} {10}}^{\,x}) = x \)

Generellt:

Exponentialekvationen \( \;\;\; 10\,^x \, = \, b \)

har lösningen: \( \qquad\qquad\quad x \, = \, \lg\,b \)

@@ Rad 6: / Rad 6: @@
 {{Not selected tab|[[3.4 Quiz till 10-logaritmer, ver 2|Quiz]]}}
 {{Not selected tab|[[3.4 Övningar till 10-logaritmer|Övningar]]}}
-{{Not selected tab|     }}
+{{Not selected tab|[[Logaritmlagarna|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 | style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 |}
@@ Rad 15: / Rad 15: @@
 {{Not selected tab|     }}
 {{Not selected tab|     }}
-{{Not selected tab|[[Logaritmlagarna|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
+{{Not selected tab|     }}
 | style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 |}