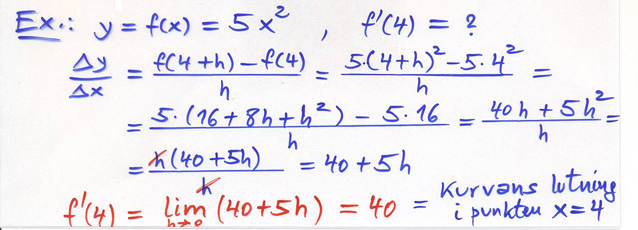Skillnad mellan versioner av "2.4 Derivatans definition"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 149: | Rad 149: | ||
<big> <span style="color:blue"><u>Ex.:</u> <math> \quad y \, = \, f(x) \, = \, 5\,x^2 \quad </math> som ovan, <u>men:</u> <math> \qquad f\,'({\color{Red} x}) \, = \, {\rm ?} \qquad \color{Red} x \, = \, \color{Red}{\rm variabel} </math> </span> </big> | <big> <span style="color:blue"><u>Ex.:</u> <math> \quad y \, = \, f(x) \, = \, 5\,x^2 \quad </math> som ovan, <u>men:</u> <math> \qquad f\,'({\color{Red} x}) \, = \, {\rm ?} \qquad \color{Red} x \, = \, \color{Red}{\rm variabel} </math> </span> </big> | ||
| − | <div style="border:1px solid black;display:inline-table;margin-left: | + | <div style="border:1px solid black;display:inline-table;margin-left: 50px;"> [[Image: DerivatDef3_50a.jpg]] </div> |
Exempel på att derivatan av en andragradsfunktion (parabel) är en linjär funktion (rät linje). | Exempel på att derivatan av en andragradsfunktion (parabel) är en linjär funktion (rät linje). | ||
| − | Ett annat exempel på detta hade vi redan sett i [[2.1_Lösning_till_Aktiviteten_Introduktion_till_derivata|<b><span style="color:blue">Lösningen till Aktiviteten (punkt 6)</span></b>]] | + | Ett annat exempel på detta hade vi redan sett i [[2.1_Lösning_till_Aktiviteten_Introduktion_till_derivata|<b><span style="color:blue">Lösningen till Aktiviteten (punkt 6)</span></b>]]. Se generell [[2.4_Derivatans_definition#Sats:|<b><span style="color:blue">sats</span></b>]] nedan. |
</small></div> | </small></div> | ||
Versionen från 5 november 2017 kl. 12.40
| << Förra avsnitt | Genomgång | Övningar | Nästa avsnitt >> |
Lektion 15 Derivatans definition I
Lektion 16 Derivatans definition II
Från genomsnittlig till momentan förändringshastighet
Exempel OljetankEn oljetank läcker genom ett hål i tankens botten enligt:
där \( \; \quad \! x \, = \, {\rm Tiden\;i\;minuter} \)
Beräkna ett bra närmevärde till oljans utströmningshastighet när den är störst, t.ex. genom att beräkna oljans genomsnitt- liga utströmningshastighet i det lilla intervallet \( \, \color{Red} {0 \,\leq\, x \,\leq\, 0,1} \, \). |
 |
Lösning:
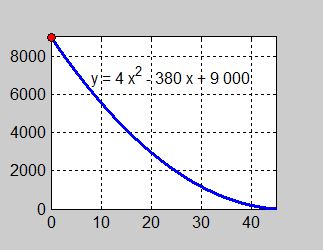
Oljans utströmningshastighet är störst när volymen och därmed trycket på hålet är störst, dvs i början.
Även grafen visar att kurvans lutning är brantast vid tiden \( \, x = 0\, \) när oljan har den största volymen \( \, 9\,000 \) liter.
Men vi kan inte beräkna utströmningshastigheten vid tiden \( \, x = 0 \, \) därför att \( x = 0 \) inte är något intervall utan en punkt.
Hastigheten vid tidpunkten \( \, x = 0 \, \) kallas för ögonblicklig eller momentan förändringshighet.
Vi kan närma oss den genom att beräkna den genomsnittliga utströmningshastigheten i det lilla intervallet \( \, \color{Red} {0 \,\leq\, x \,\leq\, 0,1} \, \):
\( f\,(\color{Red} 0) = 4 \cdot \color{Red} 0\,^2 - 380 \cdot \color{Red} 0 + 9\,000 = 9\,000 \qquad\qquad\qquad\qquad\qquad x_1 \, = \, 0\)
\( f\,(\color{Red} {0,1}) = 4 \cdot \color{Red} {0,1}\,^2 - 380 \cdot \color{Red} {0,1} + 9\,000 = 8962,04 \qquad\qquad\qquad h \, = \, 0,1\)
\( \displaystyle {\Delta y \over \Delta x} = \boxed{\displaystyle \frac{f(x_1 + h) \, - \, f(x_1)}{h}} = {f(0 + 0,1) - f(0) \over 0,1} = {f(0,1) - f(0) \over 0,1} = {8962,04 - 9000 \over 0,1} = {-37,96 \over 0,1} = \color{Red} {-379,6} \)
I intervallet \( \, \color{Red} {0 \leq x \leq 0,1} \, \) sjunker oljans volym med \( \, 379,6\, \) liter per minut.
- Faktiskt är \( \, \color{Red} {-379,6} \, \) inget dåligt närmevärde, för det exakta värdet kommer att visa sig vara \( \, \color{Red} {-380} \, \), se nedan: Lösning 2).
- För att få det exakta värdet använder vi limes och låter intervallets längd gå mot \( \, 0\, \): \( \quad \color{Red} {\boxed{h \to 0}} \)
Derivatan i en punkt = Derivatan som ett tal
Exempel Oljetank (se ovan)
1) Ställ upp oljans genomsnittliga utströmningshastighet i intervallet \( \, \color{Red}{0 \,\leq\, x \,\leq\, h} \, \) som ett uttryck i \( \, h \, \).
2) Beräkna oljans momentana utströmningshastighet i punkten \( \, x = 0 \) genom att i uttrycket ovan låta \( \, h \, \) gå mot \( \, 0 \).
Lösning:
1) Den allmänna definitionen av genomsnittlig förändringshastighet är:
- \[ {\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h} \qquad {\rm i\;\;intervallet } \qquad x_1 \,\leq\, x \,\leq\, x_1 + h \]
- I exemplet Oljetank har vi \( \, x_1 = 0 \). Därför:
- \[ {\Delta y \over \Delta x} \; = \; {f(0 + h) \, - \, f(0) \over h} \; = \; {f(h) \, - \, f(0) \over h} \qquad {\rm i\;\;intervallet } \qquad \color{Red}{0 \,\leq\, x \,\leq\, h} \]
- För \( \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, \) får vi \( \, f\,(h) \, = \, 4\,h^2 - 380\,h + 9\,000 \, \) och \( \, f\,(0) \, = \, 9\,000 \).
- Då blir oljans genomsnittliga utströmningshastighet i intervallet \( 0 \,\leq\, x \,\leq\, h \, \):
- \[ {\Delta y \over \Delta x} \,=\, {f(h) \, - \, f(0) \over h} \,=\, {4\,h^2 - 380\,h + 9\,000 \,-\, 9\,000 \over h} \,=\, {4\,h^2 - 380\,h \over h} \,=\, {\color{Red} h\,(4\,h - 380) \over \color{Red} h} \,=\, \color{Red}{4\,h - 380} \]
2) Nu låter vi i uttrycket \( 4\,h - 380 \) för den genomsnittliga utströmningshastigheten \( \, h\, \) gå mot \( 0 \)
- för att få oljans momentana utströmningshastighet i \( \, x = 0\, \). Dvs vi beräknar gränsvärdet:
- \[ \qquad \displaystyle \lim_{h \to 0}\, {(\color{Red}{4\,h - 380})} \,=\, -\,380 \]
\( \quad -\,380\, \) är oljans momentana utströmningshastighet i \( \, x = 0 \, \). Dvs vid denna tidpunkt sjunker oljan med exakt \( \, 380\, \) liter per minut.
- Ett annat ord för den momentana utströmningshastigheten är derivatan:
Funktionen \( \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, \) har i punkten \( \, x = 0 \; \) derivatan \( \; -\,380 \; \).
Man skriver: \( \; f\,{\color{Red} '}(0) \,=\, -\,380 \; \) och läser: "\( \, f \) prim av \( \, 0 \, \) är \( \; -\,380 \; \)" , där \( {\color{Red} '} \; \) är symbolen för derivatan.
\( f\,{\color{Red} '}(0) \, \) är derivatan av \( \, f\,(x) \, \) i punkten \( \, x = 0 \; \) och är talet \( \; -\,380 \; \) .
\( f\,{\color{Red} '}(a) \, \) är derivatan av \( \, f\,(x) \, \) i punkten \( \, x = a = {\rm const.} \; \) och är \( \; \displaystyle \lim_{h \to 0}\,{f(a + h) \, - \, f(a) \over h} \; \) .
Sammanfattning:
Vi får derivatan av \( \, f(x) \, \) i punkten \( \, x = a\, \) genom att ta två steg:
1) Att ställa upp den genomsnittliga förändringshastigheten \( \, \displaystyle{{\color{Red} {\Delta y \over \Delta x}}} \, \) för \( \, f(x) \, \) i intervallet \( \, a \,\leq\, x \,\leq\, h \, \) som ett uttryck i \( \, h \, \).
2) Att beräkna detta uttrycks gränsvärde för \( \, h \to 0 \, \): \( \qquad\qquad\qquad\qquad\qquad {\color{Red} {\boxed{ \displaystyle{ \lim_{h \to 0} \, \frac{\Delta y}{\Delta x} \; = \; f\,'(a) } } } } \, \)
Ett enklare exempel
I de två exemplen ovan beräknade vi derivatan i en punkt, i \( \, x = 0 \, \) i det första och i \( \, x = 4 \, \) i det andra exemplet. Resultatet blev ett tal.
Nu ska vi betrakta denna punkt inte längre som en konstant utan som en variabel \( \, x \, \). Resultatet kommer då att bli en ny funktion av \( \, x \).
Man tillämpar derivatans definition i en punkt på varenda punkt på \( \, x\)-axeln. Tänker man sig alla dessa derivatvärden tilldelade sina respektive \( \, x\)-värden, bildar denna tilldelning en ny funktion som är den ursprungliga funktionens derivata, fast inte längre som ett tal utan som ett uttryck i \( \, x \).
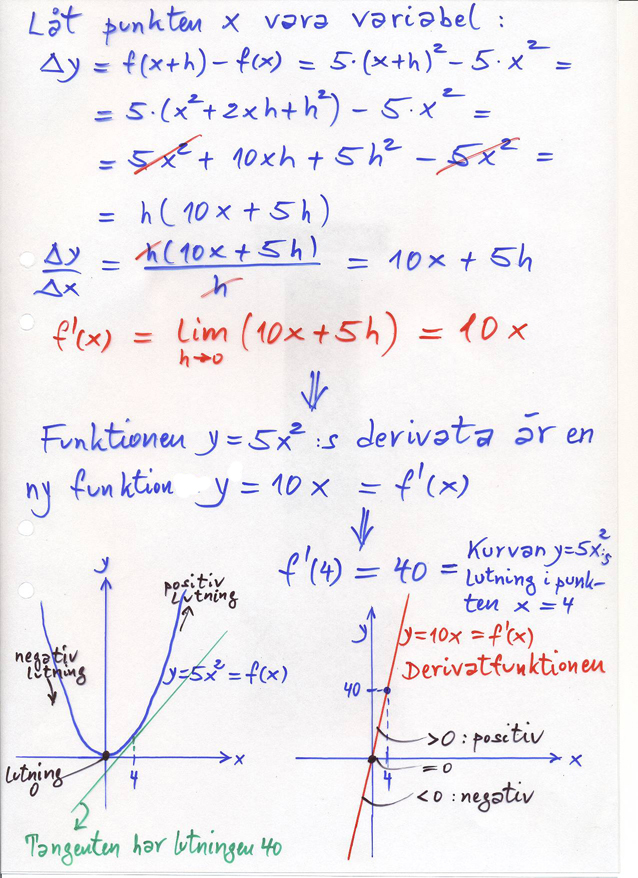
Derivatan som en ny funktion
Ex.: \( \quad y \, = \, f(x) \, = \, 5\,x^2 \quad \) som ovan, men: \( \qquad f\,'({\color{Red} x}) \, = \, {\rm ?} \qquad \color{Red} x \, = \, \color{Red}{\rm variabel} \)
Exempel på att derivatan av en andragradsfunktion (parabel) är en linjär funktion (rät linje).
Ett annat exempel på detta hade vi redan sett i Lösningen till Aktiviteten (punkt 6). Se generell sats nedan.
Derivatans allmänna definition
Derivatan av funktionen \( \, y = f\,(x) \, \) är \( \, \displaystyle f\,{\color{Red} '}(x) \; = \; \lim_{h \to 0}\,\,{f(x + h) \, - \, f(x) \over h} \, \), där
\( {\color{Red} '} \; \) är symbolen för derivatan. \( \;\, f\,{\color{Red} '}(x) \; \) är en ny funktion och läses: "\( f \) prim av \( \, x \, \)" .
Som man ser är uttrycket i limes, funktionens genomsnittliga förändringshastighet \( \, \displaystyle{\Delta y \over \Delta x} \, \) i intervallet mellan \( \, x \, \) och \( \, h \).
Exempel Oljetank (utvidgat)
Utströmningen av olja genom ett hål i oljetankens botten beskrivs av funktionen:
- \[ y \, = \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \]
a) Ställ upp funktionens genomsnittliga förändringshastighet \( \, \displaystyle{\Delta y \over \Delta x} \, \) som ett uttryck i \( \, x \, \) och \( \, h \).
b) Ange derivatan av \( \, f\,(x) \, \) som en ny funktion av \( \, x \, \) genom att i \( \, \displaystyle{\Delta y \over \Delta x} \, \) låta \( \, h \, \) gå mot \( \, 0 \).
- Rita grafen till derivatans funktion
Lösning:
a) Vi ställer upp de deluttryck som ingår i \( \, \displaystyle{\Delta y \over \Delta x} \, = \, {f(x + h) \, - \, f(x) \over h} \, \) och förenklar dem:
- \[ \begin{array}{lcl} f(x + h) & = & 4\,(x+h)^2 - 380\,(x+h) + 9\,000 = 4\,(x^2 + 2\,x\,h + h^2) - 380\,x - 380\,h + 9\,000 = \\ & = & 4\,x^2 + 8\,x\,h + 4\,h^2 - 380\,x - 380\,h + 9\,000 \\ f(x + h) - f(x) & = & 4\,x^2 + 8\,x\,h + 4\,h^2 - 380\,x - 380\,h + 9\,000 - (4\,x^2 - 380\,x + 9\,000) = \\ & = & 4\,x^2 + 8\,x\,h + 4\,h^2 - 380\,x - 380\,h + 9\,000 - 4\,x^2 + 380\,x - 9\,000 \;\;\, =\\ & = & 8\,x\,h + 4\,h^2 - 380\,h \, = \, h\,(8\,x + 4\,h - 380) \\ \displaystyle \frac{f(x + h) - f(x)}{h} & = & \displaystyle \frac{h\,(8\,x + 4\,h - 380)}{h} \, = \, 8\,x + 4\,h - 380 \end{array}\]
b) Nu beräknar vi gränsvärdet:
Vi kan sammanfatta: Funktionen \( \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, \) har derivatan \( \qquad\qquad\; f\,'\,(x) = 8\,x - 380 \; \) Derivatan av 2:a gradsfunktionen är en linjär funktion vilket även bekräftas av graferna. |
Fil:Oljetank derivataa.jpg |
För tredje gången får vi en bekräftelse på följande sats som kommer att bevisas generellt i nästa avsnitt:
Sats:
Derivatan av en andragradsfunktion är en linjär funktion.
Det första exemplet på denna sats fanns i (den genomsnittliga) hastighetsfunktionens graf till Yulias hopp från 10 m-torn, se Lösning till Aktiviteten (punkt 6).
Det andra exemplet var när vi i Derivatan som en ny funktion algebraiskt bestämde derivatan \( \, y\,' = \, 10\,x \, \) av funktionen \( \, y \, = \, 5\,x^2 \, \).
Dessutom kan vi verifiera \( f\,'(0)\):s värde som vi inledningsvis beräknade i Exempel Oljetank genom att i derivatans funktion \( f\,'(x) = 8 x - 380 \) sätta in \( \, x = 0 \) :
- \[ f\,'(0) \, = \, 8 \cdot 0 - 380 \,=\, 0 - 380 \,=\, -\,380 \]
I avsnitt 2.2, Exempel 3 d) hade vi fått \( -\,379,6\, \) för den genomsnittliga hastigheten i intervallet \( \, 0 \,\leq\, x \,\leq\, 0,1 \, \) som ett närmevärde för derivatan i \( \, x = 0 \).
Detta närmevärde hade blivit ännu precisare om vi hade valt t.ex. intervallet \( \, 0 \,\leq\, x \,\leq\, 0,01 \, \) eller \( \, 0 \,\leq\, x \,\leq\, 0,001 \, \) osv.
Det exakta värdet \( -\,380 \, \) fås genom att i intervallet \( \, 0 \,\leq\, x \,\leq\, h \, \) låta \( \, h \to 0 \).
I exemplet Oljetank är oljans utströmningshastighet derivatans fysikaliska tolkning. Men derivatan har även en geometrisk tolkning:
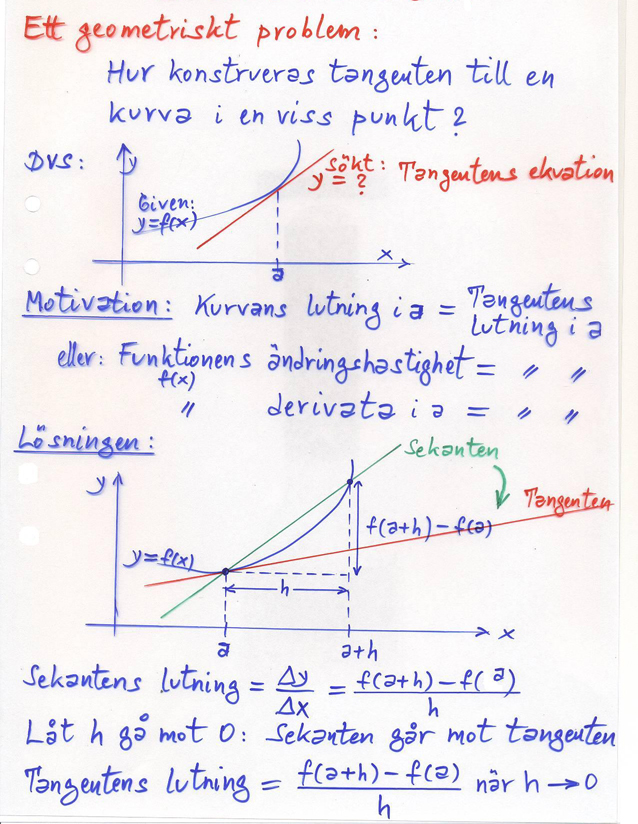
Från sekanten till tangenten
En rät linje som skär en kurva i två punkter kallas för sekant. En rät linje som "berör" kurvan i en punkt kallas för tangent.
Lutningen till en kurva \( \, y = f\,(x)\) i en viss punkt \( \, x = a \, \) definieras som tangentens lutning i denna punkt.
Denna lutning fås genom att först beräkna sekantens lutning och sedan låta sekanten gå över till tangenten \(-\) en gränsprocess.
Sedan kan vi med tangentens lutning samt punkten \( \, (a,\,f(a)) \, \) ställa upp tangentens ekvation.
Resultat:
Tangentens lutning i punkten \( \, x = a \, \) är derivatan av \( \, f\,(x) \, \) i denna punkt:
\( \qquad\qquad\qquad\quad \displaystyle f\,'(a) \, \; = \; \lim_{h \to 0}\,{f(a + h) \, - \, f(a) \over h} \)
Tangentens ekvation
Hur man, efter att ha bestämt tangentens lutning med hjälp av derivatan, ställer upp tangentens ekvation, är en Matte 2-uppgift som kan läsas t.ex. i Lösning till Aktiviteten, punkt 8-10: Geometrisk tolkning.
Internetlänkar
http://www.youtube.com/watch?v=OyKmc2bPWe0
http://www.youtube.com/watch?v=8of_svLfcjk
http://www.youtube.com/watch?v=OY8CeLUxE64&feature=related
http://www.youtube.com/watch?v=2wH-g60EJ18&feature=related
http://www.larcentrum.org/Safir/MA1203W/htm/m03_deriv1/m03_deriv_definition.htm
http://www.naturvetenskap.org/index.php?option=com_content&view=article&id=129&Itemid=132
Copyright © 2011-2017 Taifun Alishenas. All Rights Reserved.
