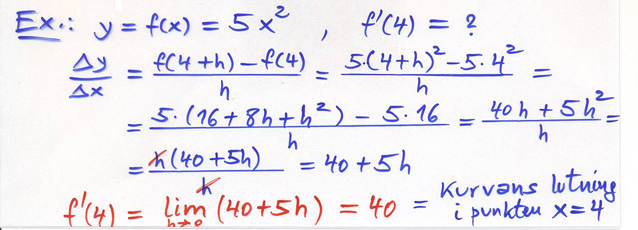Skillnad mellan versioner av "2.4 Derivatans definition"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 260: | Rad 260: | ||
<b><span style="color:red">Kurvans lutning</span></b> i en viss punkt <math> \, x = a \, </math> definieras som <b><span style="color:red">tangentens lutning</span></b> i denna punkt. | <b><span style="color:red">Kurvans lutning</span></b> i en viss punkt <math> \, x = a \, </math> definieras som <b><span style="color:red">tangentens lutning</span></b> i denna punkt. | ||
| − | Historiskt har utvecklingen av <b><span style="color:red">Analysen</span></b> <math>-</math> den gren av matematiken som handlar om | + | Historiskt har utvecklingen av <b><span style="color:red">Analysen</span></b> <math>-</math> den gren av matematiken som handlar om derivator och integraler och som [https://sv.wikipedia.org/wiki/Isaac_Newton <b><span style="color:blue">Newton</span></b>] och [https://sv.wikipedia.org/wiki/Gottfried_Wilhelm_von_Leibniz <b><span style="color:blue">Leibniz</span></b>] på 1700-talet la grunden till <math>-</math> inspirerats av följande frågeställning: |
<div class="ovnA"> | <div class="ovnA"> | ||
Versionen från 16 februari 2019 kl. 16.26
Innehåll
| << Förra avsnitt | Genomgång | Övningar | Nästa avsnitt >> |
Från genomsnittlig till momentan förändringshastighet
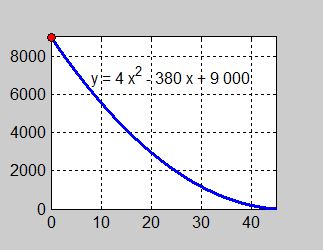
Exempel Oljetank (forts.)En oljetank läcker genom ett hål i tankens botten enligt:
där \( \; \quad \! x \, = \, {\rm Tiden\;i\;minuter} \)
Beräkna ett bra närmevärde till oljans utströmningshastighet när den är störst, t.ex. genom att beräkna oljans genomsnitt- liga utströmningshastighet i det lilla intervallet \( \, \color{Red} {0 \,\leq\, x \,\leq\, 0,1} \, \). |
 |
Lösning:
- Oljans utströmningshastighet är störst när volymen och därmed trycket på hålet är störst, dvs i början.
- Även grafen visar att kurvans lutning är brantast vid tiden \( \, x = 0\, \) när oljan har den största volymen \( \, 9\,000 \) liter.
Hastigheten vid en viss tidpunkt, t.ex. \( \, x = 0 \, \), kallas för ögonblicklig eller momentan förändringshighet.
- Den momentana utströmningshastigheten vid tidpunkten \( \, x = 0 \, \) kan vi inte beräkna än, därför att \( x = 0 \) är en punkt, inget intervall.
- Däremot kan vi närma oss den genom att beräkna den genomsnittliga utströmningshastigheten i det lilla intervallet \( \, \color{Red} {0 \,\leq\, x \,\leq\, 0,1} \, \):
- \[ f\,(\color{Red} 0) = 4 \cdot \color{Red} 0\,^2 - 380 \cdot \color{Red} 0 + 9\,000 = 9\,000 \qquad\qquad\qquad\qquad\qquad x_1 \, = \, 0\]
- \[ f\,(\color{Red} {0,1}) = 4 \cdot \color{Red} {0,1}\,^2 - 380 \cdot \color{Red} {0,1} + 9\,000 = 8962,04 \qquad\qquad\qquad h \, = \, 0,1\]
- \[ \displaystyle {\Delta y \over \Delta x} = \boxed{\displaystyle \frac{f(x_1 + h) \, - \, f(x_1)}{h}} = {f(0 + 0,1) - f(0) \over 0,1} = {f(0,1) - f(0) \over 0,1} = {8962,04 - 9000 \over 0,1} = {-37,96 \over 0,1} = \color{Red} {-379,6} \]
- I intervallet \( \, \color{Red} {0 \leq x \leq 0,1} \, \) sjunker oljans volym med \( \, 379,6\, \) liter per minut.
- Faktiskt är \( \, \color{Red} {-379,6} \, \) inget dåligt närmevärde, för det exakta värdet kommer att visa sig vara \( \, \color{Red} {-380} \, \), se nedan: Lösning 2).
- Ett ännu bättre närmevärde skulle vi få om vi valde en ännu mindre intervallängd, t.ex. \( \, h = 0,01 \, \) osv. : Jobbigt förfarande!
- För att få det exakta värdet använder vi limes och låter intervallängden gå mot \( \, 0\, \): \( \quad \color{Red} {\boxed{h \to 0}} \)
Derivatan i en punkt = Derivatan som ett tal
Exempel Oljetank (se ovan)
1) Ställ upp oljans genomsnittliga utströmningshastighet i intervallet \( \, \color{Red}{0 \,\leq\, x \,\leq\, h} \, \) som ett uttryck i \( \, h \, \).
2) Beräkna oljans momentana utströmningshastighet i punkten \( \, x = 0 \) genom att i uttrycket ovan låta \( \, h \, \) gå mot \( \, 0 \).
Lösning:
1) Den allmänna definitionen av genomsnittlig förändringshastighet är:
- \[ {\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h} \qquad {\rm i\;\;intervallet } \qquad x_1 \,\leq\, x \,\leq\, x_1 + h \]
- I exemplet Oljetank har vi \( \, x_1 = 0 \). Därför:
- \[ {\Delta y \over \Delta x} \; = \; {f(0 + h) \, - \, f(0) \over h} \; = \; {f(h) \, - \, f(0) \over h} \qquad {\rm i\;\;intervallet } \qquad \color{Red}{0 \,\leq\, x \,\leq\, h} \]
- För \( \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, \) får vi \( \, f\,(h) \, = \, 4\,h^2 - 380\,h + 9\,000 \, \) och \( \, f\,(0) \, = \, 9\,000 \).
- Då blir oljans genomsnittliga utströmningshastighet i intervallet \( 0 \,\leq\, x \,\leq\, h \, \):
- \[ {\Delta y \over \Delta x} \,=\, {f(h) \, - \, f(0) \over h} \,=\, {4\,h^2 - 380\,h + 9\,000 \,-\, 9\,000 \over h} \,=\, {4\,h^2 - 380\,h \over h} \,=\, {\color{Red} h\,(4\,h - 380) \over \color{Red} h} \,=\, \color{Red}{4\,h - 380} \]
2) Nu låter vi i uttrycket \( 4\,h - 380 \) för den genomsnittliga utströmningshastigheten \( \, h\, \) gå mot \( 0 \)
- för att få oljans momentana utströmningshastighet i \( \, x = 0\, \). Dvs vi beräknar gränsvärdet:
- \[ \qquad \displaystyle \lim_{h \to 0}\, {(\color{Red}{4\,h - 380})} \,=\, -\,380 \]
\( \quad -\,380\, \) är oljans momentana utströmningshastighet i \( \, x = 0 \, \). Dvs vid denna tidpunkt sjunker oljan med exakt \( \, 380\, \) liter per minut.
- Ett annat ord för den momentana utströmningshastigheten är derivatan:
Funktionen \( \, f\,(x) \, = \, 4\,x^2 - 380\,x + 9\,000 \, \) har i punkten \( \, x = 0 \; \) derivatan \( \; -\,380 \; \).
Man skriver: \( \; f\,\color{Red} '(0) \,=\, -\,380 \; \) och läser "\( \, f \) prim av \( \, 0 \, \) är \( \; -\,380 \; \)" , där \( \color{Red} ' \; \) är symbolen för derivatan.
Derivatan av \( \, f\,(x) \, \) i punkten \( \, x = \color{Red} 0 \; \) är \( \; \displaystyle f\,{\color{Red} '}(\color{Red} 0) \, = \, \lim_{h \to 0}\,{f(\color{Red} 0 + h) \, - \, f(\color{Red} 0) \over h} \; = \; \color{Red} {-\,380} \) .
Generellt:
Derivatan av \( \, f\,(x) \, \) i punkten \( \, x = \color{Red} a = {\rm const.} \; \) är \( \; \displaystyle f\,{\color{Red} '}(\color{Red} a) \, = \, \lim_{h \to 0}\,{f(\color{Red} a + h) \, - \, f(\color{Red} a) \over h} \; = \; \) ett tal.
Ett enklare exempel
I de två exemplen ovan beräknade vi derivatan i en punkt, i \( \, x = 0 \, \) i det första och i \( \, x = 4 \, \) i det andra exemplet. Resultatet blev ett tal.
Sammanfattning:
Vi får derivatan av \( \, f(x) \, \) i punkten \( \, x = a = {\rm const.} \, \) genom att ta två steg:
1) Att ställa upp den genomsnittliga förändringshastigheten \( \;\, \displaystyle \frac{\Delta y}{\Delta x} = \frac{f(a + h) \, - \, f(a)}{h} \;\, \) i intervallet \( \, a \,\leq\, x \,\leq\, a+h \, \) som ett uttryck i \( \, h \, \).
2) Att beräkna detta uttrycks gränsvärde för \( \, h \to 0 \, \): \( \qquad\qquad\quad \displaystyle \lim_{h \to 0} \, {f(a + h) \, - \, f(a) \over h} \; = \; \color{Red} {f\,'(a)} \, \)
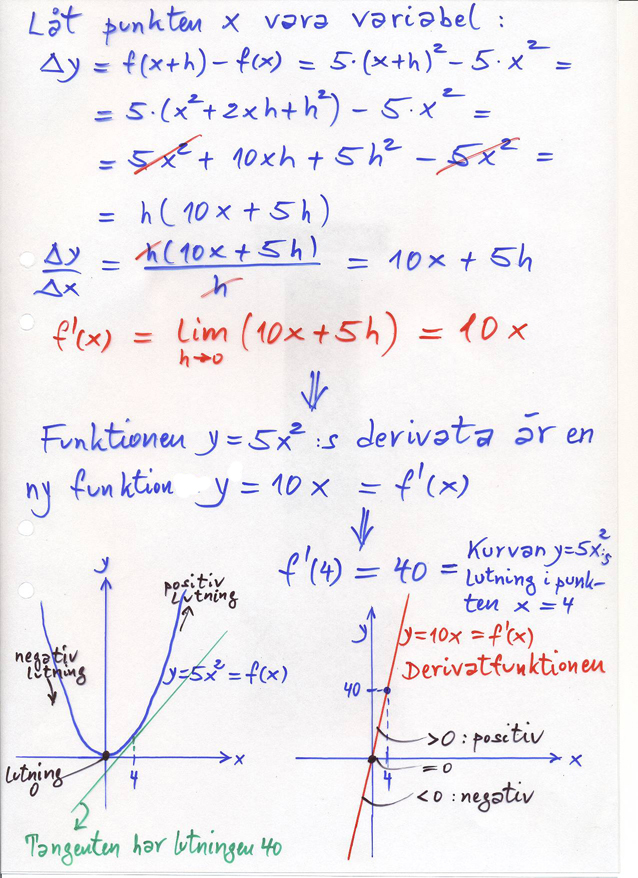
Nu ska vi betrakta punkten \( \, x = a \, \) inte längre som konstant utan som variabel. Dvs vi tillämpar derivatans definition på varenda punkt på \( \, x\)-axeln.
Tänker man sig alla dessa derivatvärden tilldelade sina respektive \( \, x\)-värden, blir resultatet en ny funktion av \( \, x \, \) som är den ursprungliga funktionens derivata.
Derivatan som en ny funktion
Ex.: \( \quad y \, = \, f(x) \, = \, 5\,x^2 \quad \) som ovan, men: \( \qquad\quad f\,'({\color{Red} x}) \, = \, {\rm ?} \qquad \color{Red} x \, = \, \color{Red}{\rm variabel} \)
Exempel på att derivatan av en andragradsfunktion (parabel) är en linjär funktion (rät linje).
Ett annat exempel på detta hade vi redan sett i Lösningen till Aktiviteten (punkt 6). Se generell sats nedan.
Derivatans allmänna definition
Derivatan av funktionen \( \, y = f\,(x) \, \) är \( \, \displaystyle f\,\color{Red} '(\color{Red} x) \; = \; \lim_{h \to 0}\,\,{f(\color{Red} x + h) \, - \, f(\color{Red} x) \over h} \, = \, \) en ny funktion,
där \( \, {\color{Red} '} \; \) är symbolen för derivatan. \( \;\, f\,{\color{Red} '}(x) \; \) läses "\( f \) prim av \( \, x \, \)" .
Som man ser är uttrycket i limes, funktionens genomsnittliga förändringshastighet \( \, \displaystyle{\Delta y \over \Delta x} \, \) i intervallet mellan \( \, x \, \) och \( \, x+h \).
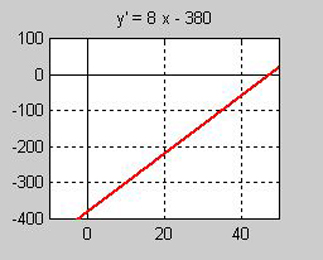
Exempel Oljetank (utvidgat)Utströmningen av olja genom ett hål i oljetankens botten beskrivs av funktionen:
a) Ställ upp funktionens genomsnittliga förändringshastighet \( \, \displaystyle{\Delta y \over \Delta x} \, \) som
b) Ange derivatan av \( \, f\,(x) \, \) som en ny funktion av \( \, x \, \) genom att i \( \, \displaystyle{\Delta y \over \Delta x} \, \)
|
\( \qquad\quad \) |  |
Lösning:
a) Vi ställer upp de deluttryck som ingår i \( \, \displaystyle{\Delta y \over \Delta x} \, = \, {f(x + h) \, - \, f(x) \over h} \, \) och förenklar dem:
- \[ \begin{array}{lcl} f(x + h) & = & 4\,(x+h)^2 - 380\,(x+h) + 9\,000 = 4\,(x^2 + 2\,x\,h + h^2) - 380\,x - 380\,h + 9\,000 = \\ & = & 4\,x^2 + 8\,x\,h + 4\,h^2 - 380\,x - 380\,h + 9\,000 \\ f(x + h) - f(x) & = & 4\,x^2 + 8\,x\,h + 4\,h^2 - 380\,x - 380\,h + 9\,000 - (4\,x^2 - 380\,x + 9\,000) = \\ & = & 4\,x^2 + 8\,x\,h + 4\,h^2 - 380\,x - 380\,h + 9\,000 - 4\,x^2 + 380\,x - 9\,000 \;\;\, =\\ & = & 8\,x\,h + 4\,h^2 - 380\,h \, = \, h\,(8\,x + 4\,h - 380) \\ \displaystyle \frac{f(x + h) - f(x)}{h} & = & \displaystyle \frac{h\,(8\,x + 4\,h - 380)}{h} \, = \, 8\,x + 4\,h - 380 \end{array}\]
Nu kan vi verifiera \( f\,'(0)\):s värde som vi inledningsvis beräknade i Exempel Oljetank genom att i derivatans funktion \( f\,'(x) = 8 x - 380 \) sätta in \( \, x = 0 \) :
- \[ f\,'(0) \, = \, 8 \cdot 0 - 380 \,=\, 0 - 380 \,=\, -\,380 \]
I avsnitt 2.2, Exempel 3 d) hade vi fått \( -\,379,6\, \) för den genomsnittliga hastigheten i intervallet \( \, 0 \,\leq\, x \,\leq\, 0,1 \, \) som ett närmevärde för derivatan i \( \, x = 0 \).
Dessutom får vi för tredje gången en bekräftelse på följande sats:
Sats:
Derivatan av en andragradsfunktion är en linjär funktion.
Bevis: Se nästa avsnitt.
Det första exemplet på denna sats fanns i (den genomsnittliga) hastighetsfunktionens graf till Yulias hopp från 10 m-torn, se Lösning till Aktiviteten (punkt 6).
Det andra exemplet var när vi i Derivatan som en ny funktion algebraiskt bestämde derivatan \( \, y\,' = \, 10\,x \, \) av funktionen \( \, y \, = \, 5\,x^2 \, \).
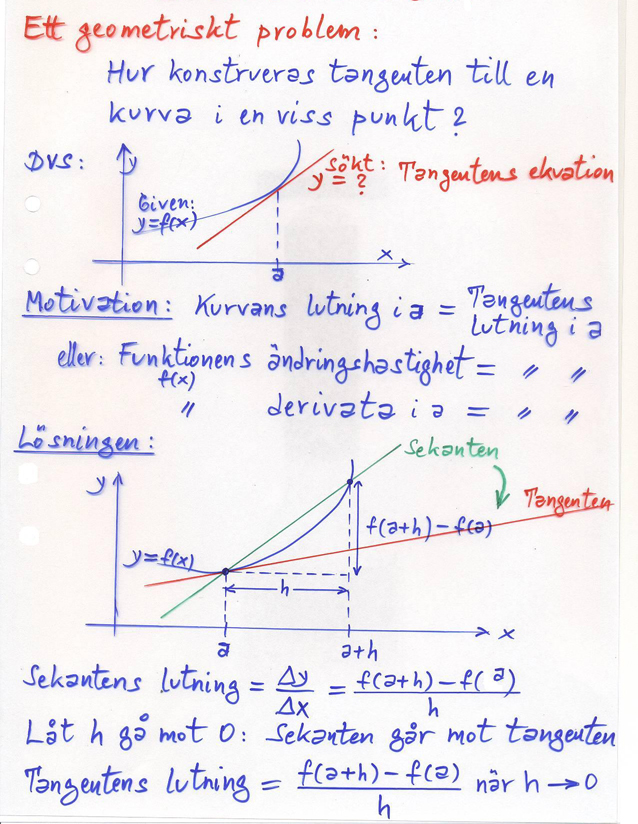
Från sekanten till tangenten
I exemplet Oljetank är oljans utströmningshastighet derivatans fysikaliska tolkning. Men derivatan har även en geometrisk tolkning:
En rät linje som skär en kurva i två punkter kallas för sekant. En rät linje som "berör" kurvan i en punkt kallas för tangent.
Kurvans lutning i en viss punkt \( \, x = a \, \) definieras som tangentens lutning i denna punkt.
Historiskt har utvecklingen av Analysen \(-\) den gren av matematiken som handlar om derivator och integraler och som Newton och Leibniz på 1700-talet la grunden till \(-\) inspirerats av följande frågeställning:
Resultat:
Tangentens lutning i punkten \( \, x = a \, \) är derivatan av \( \, f\,(x) \, \) i denna punkt:
\( \qquad\qquad\qquad\quad \displaystyle f\,'(a) \, \; = \; \lim_{h \to 0}\,{f(a + h) \, - \, f(a) \over h} \)
Som man ser fås tangentens lutning genom att först beräkna sekantens lutning och sedan låta sekanten gå över till tangenten \(-\) en gränsprocess.
Sedan kan vi med tangentens lutning samt punkten \( \, (a,\,f(a)) \, \) ställa upp tangentens ekvation.
Tangentens ekvation
Hur man, efter att ha bestämt tangentens lutning med hjälp av derivatan, ställer upp tangentens ekvation, är en Matte 2-uppgift som kan läsas t.ex. i
Internetlänkar
http://www.youtube.com/watch?v=OyKmc2bPWe0
http://www.youtube.com/watch?v=8of_svLfcjk
http://www.youtube.com/watch?v=OY8CeLUxE64&feature=related
http://www.youtube.com/watch?v=2wH-g60EJ18&feature=related
http://www.larcentrum.org/Safir/MA1203W/htm/m03_deriv1/m03_deriv_definition.htm
http://www.naturvetenskap.org/index.php?option=com_content&view=article&id=129&Itemid=132
Copyright © 2011-2018 Math Online Sweden AB. All Rights Reserved.