Skillnad mellan versioner av "2.2 Genomsnittlig förändringshastighet"
Taifun (Diskussion | bidrag) m (→Vad är genomsnittlig förändringshastighet?) |
Taifun (Diskussion | bidrag) m (→Vad är genomsnittlig förändringshastighet?) |
||
| Rad 21: | Rad 21: | ||
::Funktionens genomsnittliga förändringshastighet i detta intervall dvs: | ::Funktionens genomsnittliga förändringshastighet i detta intervall dvs: | ||
| − | :::<math> {\Delta y \over \Delta x} \; = \; {y_2 - y_1 \over x_2 - x_1} \; = \; {f(x_2) \, - \, f(x_1) \over x_2 - x_1} \; = \; </math> Förändring över intervallet <math> / </math> Intervallets längd </big> | + | :::<math> {\Delta y \over \Delta x} \; = \; {y_2 - y_1 \over x_2 - x_1} \; = \; {f(x_2) \, - \, f(x_1) \over x_2 - x_1} \; = \; </math> Förändring över intervallet <math> \big / </math> Intervallets längd </big> |
En annan form på den genomsnittliga förändringshastigheten får man om man inför den nya beteckningen <math> h\, </math> för intervallets längd: | En annan form på den genomsnittliga förändringshastigheten får man om man inför den nya beteckningen <math> h\, </math> för intervallets längd: | ||
Versionen från 8 januari 2012 kl. 19.24
| Teori | Övningar |
Vad är genomsnittlig förändringshastighet?
Givet:
- Funktionen \( y \, = \, f\,(x) \) i form av en formel, tabell eller graf.
- Något intervall på \( x\, \)-axeln med givna gränser \( x_1\, \) och \( x_2\, \) dvs\[ x_1 \,\leq\, x \,\leq\, x_2 \]
Sökt:
- Funktionens genomsnittliga förändringshastighet i detta intervall dvs:
- \[ {\Delta y \over \Delta x} \; = \; {y_2 - y_1 \over x_2 - x_1} \; = \; {f(x_2) \, - \, f(x_1) \over x_2 - x_1} \; = \; \] Förändring över intervallet \( \big / \) Intervallets längd
En annan form på den genomsnittliga förändringshastigheten får man om man inför den nya beteckningen \( h\, \) för intervallets längd:
- \[\begin{align} h & = x_2 - x_1 \qquad & | \; + \, x_1 \\ x_1 + h & = x_2 \\ \end{align}\]
Då kan funktionen \( y = f\,(x) \):s genomsnittliga förändringshastighet i intervallet \( x_1 \,\leq\, x \,\leq\, x_1 + h \) definieras som:
- \[ {\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h} \]
Vilket av de två identiska uttrycken ovan man använder beror på sammanhanget. I rent beräkningssammanhang föredras ofta den första formen, medan man i teoretiska resonemang, speciellt när man definierar derivatan exakt eller bevisar deriveringsregler, snarare använder sig av den andra formen.
Kärt barn har många namn: De två uttrycken ovan har ett antal namn som allihopa kan anses vara synonymer:
- Genomsnittlig förändringshastighet
- Förändringskvot
- Ändringskvot
- Differenskvot
Om vi kommer ihåg hur begreppet lutning till en rät linje var definierat i Matte B-kursen, kan vi säga att uttrycket ovan (ta den första formen) är inget annat än lutningen till den räta linje som ersätter kurvan \( y = f\,(x) \) i det betraktade intervallet. Dvs om man bortser från kurvans verkliga (kanske krokiga) förlopp och antar istället att det går en rät linje i det betraktade intervallet kan denna räta linjes lutning beräknas med uttrycket ovan. Den räta linjens lutning kallas då kurvans genomsnittliga förändringshastighet i det betraktade intervallet.
Exempel 1
Givet:
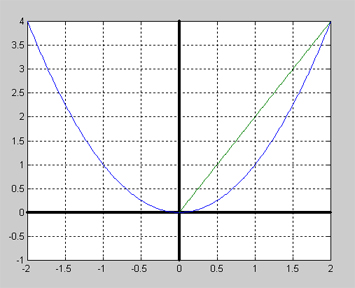
- Funktionen \( y \, = \, x^2 \)
- Intervallet \( 0 \,\leq\, x \,\leq\, 2 \)
Sökt:
- Funktionens genomsnittliga förändringshastighet i detta intervall.
Lösning:
- \[ {\Delta y \over \Delta x} \; = \; {f(2) \, - \, f(0) \over 2 - 0} \; = \; {2^2 \, - \, 0^2 \over 2 - 0} \; = \; {4 \, - \, 0 \over 2} \; = \; {4 \over 2} \; = \; 2 \]
Funktionen \( y = x^2 \, \) växer i hela intervallet \( 0 \leq x \leq 2 \) (dvs i genomsnitt) med 2 y-enheter per x-enhet. Detta är innebörden av att funktionens genomsnittliga förändringshastighet i intervallet \( 0 \leq x \leq 2 \) är 2.
Ersätter man i detta intervall kurvan med en rät linje, är det i själva verket linjens lutning som är 2. Denna lutning är identisk med kurvans genomsnittliga förändringshastighet i det betraktade intervallet.
Exempel 2
En oljetank läcker genom ett hål i tankens botten. Utströmningen av oljan beskrivs av funktionen:
- \[ y \, = \, 4\,x^2 - 380\,x + 9\,000 \]
där
- \[ x \, = \, \] Tiden i minuter
- \[ y \, = \, \] Oljans volym i liter
a) Rita grafen till funktionen som beskriver utströmningen.
b) Hur stor är oljans genomsnittliga utströmningshastighet i hela tidsintervallet från början tills tanken är tom.
c) Beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet \( 20 \leq x \leq 30 \).
d) När är oljans (genomsnittliga) utströmningshastighet störst? Ange den så noggrant som möjligt.
Lösning:
a)
b) Grafen tyder pår att tanken är tom efter ca. 45 minuter. Den exakta tiden får man genom att lösa 2:a gradsekvationen:
- \[ 4\,x^2 - 380\,x + 9\,000 = 0 \]
Räknarens ekvationslösare visar att \( x = 45\, \) är den exakta tiden. Därför är hela tidsintervallet från början tills tanken är tom \( 0 \leq x \leq 45 \). I detta intervall är oljans genomsnittliga utströmningshastighet\[ {\Delta y \over \Delta x} = {f(45) \, - \, f(0) \over 45 - 0} = {0 \, - \, 9000 \over 45} = {-9000 \over 45} = -200 \]
I hela tidsintervallet \( 0 \leq x \leq 45 \) sjunker oljans volym med 200 liter per minut.
c) I tidsintervallet \( 20 \leq x \leq 30 \) är oljans genomsnittliga utströmningshastighet:
\[ f\,(30) = 4 \cdot 30^2 - 380 \cdot 30 + 9\,000 = 1200 \]
\[ f\,(20) = 4 \cdot 20^2 - 380 \cdot 20 + 9\,000 = 3000 \]
\[ {\Delta y \over \Delta x} = {f(30) \, - \, f(20) \over 30 - 20} = {1200 \, - \, 3000 \over 30 - 20} = {-1800 \over 10} = -180 \]
I tidsintervallet \( 20 \leq x \leq 30 \) sjunker oljans volym med 180 liter per minut.
d) Grafen i a) visar att kurvans lutning är störst i början dvs vid tiden \( x = 0\, \) när oljan har mest volym, nämligen 9 000 liter. Därför är även oljans utströmningshastighet störst vid denna tidpunkt. Men denna hastighet är inte längre genomsnittlig i något intervall utan ögonblicklig vid en viss tidpunkt eller momentan.
För att beräkna den momentana och därmed den exakta utströmningshastigheten vid tiden \( x = 0\, \) måste man bestämma funktionen \( y\, \):s exakta derivata, vilket vi inte lärt oss ännu.
För att approximera den momentana utströmningshastigheten vid tiden \( x = 0\, \) så noggrant som möjligt måste vi välja ett så litet tidsintervall som möjligt med \( x = 0\, \) som undre intervallgräns.
Låt oss t.ex. beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet \( 0 \leq x \leq 0,1 \):
\[ f\,(0,1) = 4 \cdot 0,1^2 - 380 \cdot 0,1 + 9\,000 = 8962,04 \]
\[ {\Delta y \over \Delta x} = {f(0,1) \, - \, f(0) \over 0,1 - 0} = {8962,04 \, - \, 9000 \over 0,1} = {-37,96 \over 0,1} = -379,6 \]
I tidsintervallet \( 0 \leq x \leq 0,1 \) sjunker oljans volym med \( 379,6\, \) liter per minut.
Faktiskt är denna approximation inget dåligt närmevärde för den momentana utströmningshastigheten vid tiden \( x = 0\, \), för det exakta värdet är \( -380\, \). I nästa avsnitt kommer vi att lära oss hur man får reda på det.
Internetlänkar
http://ingforum.haninge.kth.se/matCD/F%F6rel%E4sning01.pdf
http://www.iceclimbers.net/fil/matematik_c/12.genomsnittlig_forandringshastighet.pdf
Copyright © 2010-2012 Taifun Alishenas. All Rights Reserved.