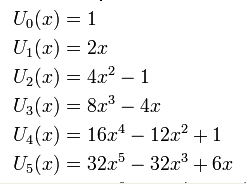Skillnad mellan versioner av "1.1 Polynom"
Taifun (Diskussion | bidrag) m (→Allmän definition) |
Taifun (Diskussion | bidrag) m (→Allmän definition) |
||
| Rad 143: | Rad 143: | ||
:: <math>a_0 = 9\,</math> | :: <math>a_0 = 9\,</math> | ||
| − | <b>Konvention:</b> Som redan sades inledningsvis brukar man, för att höja läsligheten och hålla sig till en bra struktur, börja med den | + | <b>Konvention:</b> Som redan sades inledningsvis brukar man, för att höja läsligheten och hålla sig till en bra struktur, börja med den term som har den högsta x-potensen, skriva termerna i avtagande exponentordning och avsluta med den konstanta termen, även om det ur ren beräkningssynpunkt är irrelevant i vilken ordning man skriver ett polynoms termer. |
== Polynomfunktioner == | == Polynomfunktioner == | ||
Versionen från 22 juni 2014 kl. 12.33
| Teori | Övningar |
Kapitel 1 Algebra och funktioner
Innehåll
Exempel på polynom
Uttrycken nedan kallas polynom:
\[ 4\,x + 12 \]
\[ 3\,x^2 + 5\,x - 16 \]
\[ 8\,x^3 + 4\,x^2 - 7\,x + 6\]
\[ 3\,x^4 - 8\,x^3 + 12\,x^2 - 54\,x + 9 \]
För läslighetens och strukturens skull brukar man inleda ett polynom med den högsta x-potensen och fortsätta i fallande ordning efter exponenterna.
Uppgift: Utveckla följande uttryck till ett polynom\[ 6\,x^3 - 4\,x^2\,(3\,x + 8) + 2\,x\,(5 + 9\,x) \]
Lösning: Vi löser upp parenteserna, sammanfogar de termer som går att sammanfoga och ordnar x-potenserna i fallande ordning\[ 6\,x^3 - 4\,x^2\,(3\,x + 8) + 2\,x\,(5 + 9\,x) = \,6\,x^3 -\,12\,x^3\,-\,32\,x^2 +\,10\,x\,+\,18\,x^2 = \underline{-6\,x^3 - 14\,x^2 +\,10\,x} \]
Grad
Den högst förekommande x-potensen i ett polynom dvs den största exponenten till x bland polynomets alla termer kallas polynomets grad.
Polynomet \( x^4 - 29\;x^2 + 100 \) har graden 4 eftersom den högst förekommande x-potensen har exponenten 4.
I de inledande exemplen ovan har polynomen graderna 1, 2, 3 och 4 i den ordning de är angivna.
Koefficienter
Talen framför x-potenserna kallas polynomets koefficienter.
Polynomet \( 4\,x + 12 \) har koefficienterna \(4\,\) och \(12\,\).
Polynomet \( 3\,x^2 + 5\,x - 16 \) har koefficienterna \(3, 5\,\) och \(-16\,\).
Ett polynoms värde
Eftersom ett polynom är en speciell form av ett uttryck är ett polynoms värde inget annat än uttryckets värde. Ett polynom har inget givet värde för sig utan får ett värde för något specificerat värde för \(x\,\).
Uppgift: Följande polynom är givet\[ 8\,x^3 - 4\,x \]
Beräkna polynomets värde för \( x = 0,5\, \).
Lösning: Vi sätter in \( 0,5\,\) för \(x\,\) i polynomets alla termer och beräknar polynomets värde\[ 8 \cdot 0,5^3 - 4 \cdot 0,5 = 8 \cdot 0,125 - 2 = 1 - 2 = -1 \,\]
Det givna polynomets värde för \( x = 0,5\, \) är \( -1\,\). För andra värden på \(x\,\) kommer polynomet att ha andra värden.
Att räkna med polynom
Man räknar med polynom precis på samma sätt som man gör det med uttryck därför att polynom är en speciell form av uttryck. Man kan addera, subtrahera och multiplicera polynom med varandra. Resultatet blir ett nytt polynom.
Summan, differensen och produkten av polynom är alltid ett polynom.
Ex.: Två polynom är givna\[ 6\,x^2 + 2\,x - 3 \]
- \[ -6\,x^2 - 3\,x + 4 \]
Bilda deras summa, differens och produkt.
Summa = resultat av addition:
\( (6\,x^2\,+\,2\,x\,-\,3)\,+\,(-6\,x^2\,-\,3\,x\,+\,4) = 6\,x^2\,+\,2\,x\,-\,3\,-\,6\,x^2\,-\,3\,x\,+\,4 = -\,x\,+\,1 \)
Differens = resultat av subtraktion:
\( (6\,x^2\,+\,2\,x\,-\,3)\,-\,(-6\,x^2\,-\,3\,x\,+\,4) = 6\,x^2\,+\,2\,x\,-\,3\,+\,6\,x^2\,+\,3\,x\,-\,4 = 12\,x^2\,+\,5\,x\,-\,7 \)
Produkt = resultat av multiplikation:
\( (6\,x^2\,+\,2\,x\,-\,3)\,\cdot\,(-6\,x^2\,-\,3\,x\,+\,4) = -36\,x^4\,-\,18\,x^3\,+\,24\,x^2\,-\,12\,x^3\,-\,6\,x^2\,+\,8\,x\,+\,18\,x^2\,+\,9\,x\,-\,12 = \)
\( = -36\,x^4\,-\,30\,x^3\,+\,36\,x^2\,+\,17\,x\,-\,12 \)
Det man gör här hela tiden är att först lösa upp parenteserna och sedan sammanfoga de termer som går att sammanfoga, det är de termer som har samma exponent. Att lösa upp parenteserna innebär i additionsexemplet att ta bort parenteserna utan åtgärd. Vid subtraktion däremot måste man vända om alla förtecken i den parentes som minustecknet står framför, allt enligt algebrans lagar för \( + \) och \( - \) . Vid multiplikation multipliceras varje term i den första parentesen in i den andra parentesen, dvs med alla termer i den, allt enligt algebrans distributivlag.
Som man ser blir alla resultat polynom. Vid addition och subtraktion blir resultatens grad samma eller mindre än utgångspolynomen. I additionsexemplet blir graden mindre eftersom de kvadratiska termerna tar ut varandra. Multiplikationen däremot förstorar graden. I vårt exempel är faktorerna 2:a gradspolynom medan deras produkt blir av graden 4. Generellt gäller det att produktpolynomets grad blir m + n om faktorernas grader är m och n, vilket är en konsekvens av första potenslagen.
Kvoten (resultatet av division) av två polynom är i regel inget polynom.
Till skillnad från addition, subtraktion och multiplikation av två (eller flera) polynom som alltid ger ett polynom, ger division av två polynom i regel inte ett polynom. Det enklaste exemplet är uttrycket:
- \[ 1 \over x \]
Detta uttryck kan å ena sidan uppfattas som kvoten (resultatet av division) mellan polynomet 1 (av graden 0) och polynomet x (av graden 1). Å andra sidan är \( 1/x \) enligt potenslagarna identiskt med:
- \[ x^{-1}\, \]
Försöker man att identifiera detta som en term ser man att exponenten är negativ. Men ett polynoms termer måste ha exponenter till x som är positiva eller 0, se definitionen för term. Därför är uttrycket ovan inget polynom - ett exempel på att kvoten av två polynom i regel inte är polynom. Division av polynom leder oss till en ny klass av uttryck som \(1 \over x\,\) eller \(x^{-1}\,\) är ett exempel på.
Denna nya klass av uttryck kallas rationella uttryck och kommer att behandlas senare i avsnitt 1.3.
Allmän definition
Ordet poly betyder på latin många och nom betyder term. Så polynom är närmare bestämt en summa av många termer. Ett exempel på term är följande:
- \[ 8 \cdot x^3 \]
dvs en konstant gånger en x-potens. Generellt ser en term ut så här:
- \[ a \cdot x^n \]
Som en summa av många sådana termer är ett polynom en speciell form av ett uttryck. Generellt har ett polynom av grad \(n\,\) följande form:
- \[ a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + \quad \ldots \quad + a_1 \cdot x + a_0 \]
där \(n\,\) måste vara ett positivt heltal eller 0. Dvs \(n\,\) och därmed alla termers exponenter får varken vara negativa eller bråk (decimaltal).
Observera att uttrycket inte är ett polynom om någon term har en x-potens med negativ exponent eller ett bråk som exponent. Därför är t.ex. \( 1 \over x \) eller \( \sqrt x \) inga polynom, för \( {1 \over x} = x^{-1}\, \) och \( \sqrt x = x^{1\over2} \). Inte heller sådana uttryck som innehåller \( 1 \over x \) eller \( \sqrt x \), kan vara polynom.
Koefficienterna \(a_n\,\) är godtyckliga kända konstanter, medan \(x\,\) är en variabel som kan anta vilka värden som helst. \( a_0\, \) kallas den konstanta termen.
Det nedsänkta \(_n\,\)-et i \(a_n\,\) är en del av beteckningen och kallas index. Indicerade beteckningar använder man här för att associera koefficienten till x-potensens exponent.
Exempel: 5:e gradspolynomet
- \[ x^5 + 3\,x^4 - 8\,x^3 + 12\,x^2 - 54\,x + 9 \]
har koefficienterna:
- \[a_5 = 1\,\]
- \[a_4 = 3\,\]
- \[a_3 = -8\,\]
- \[a_2 = 12\,\]
- \[a_1 = -54\,\]
- \[a_0 = 9\,\]
Konvention: Som redan sades inledningsvis brukar man, för att höja läsligheten och hålla sig till en bra struktur, börja med den term som har den högsta x-potensen, skriva termerna i avtagande exponentordning och avsluta med den konstanta termen, även om det ur ren beräkningssynpunkt är irrelevant i vilken ordning man skriver ett polynoms termer.
Polynomfunktioner
När ett polynom tilldelas en annan variabel, säg \( y\, \) ger det upphov till en speciell typ av funktion, kallad polynomfunktion. Närmare bestämt är polynomfunktioner en generalisering samt utvidgning av de funktionstyper vi sysslat hittills med. I Matte 1c-kursen hade vi bara linjära eller 1:a gradsfunktioner av typ:
- \[ y = 4\,x + 12 \]
Till höger om likhetstecknet står ett polynom där \( x\, \) förekommer som 1:a gradspotens dvs med exponenten 1. Därför kallas \( 4 x\, \) polynomets linjära term. Dess koefficient är \( 4\, \). \( 12\, \) är polynomets konstanta term. Grafen till denna 1:a gradsfunktion är en rät linje. I Matte 2c-kursen gick vi ett steg vidare och sysslade med 2:a gradsfunktioner av typ:
- \[ y = 3\,x^2 + 5\,x - 16 \]
Här är 2 den högsta exponenten till \( x\, \). \( 3\, \) är koefficienten till den kvadratiska termen \( 3 x^2\, \), \( 5\, \) är koefficienten till den linjära termen \( 5 x\, \) och \( -16\, \) är koefficienten till den konstanta termen \( -16 x^0\, \). Grafen till denna 2:a gradsfunktion är en parabel. Redan dessa funktioner är polynomfunktioner utan att vi kallade dem så, därför att de är summor av termer som uppfyller de villkor som vi införde för n - nämligen att vara ett positivt heltal eller 0. Dvs vi har i Matte 1c och 2c sysslat med polynomfunktioner där n var 0, 1 eller 2, men inte högre. Om du undrar varför även konstanterna -16 och 12 i exemplen ovan kan anses som "termer" i den inledningsvis definierade bemärkelsen, kom ihåg att man kan skriva -16 som:
- \[ -16 \cdot x^0 \]
Att man kan göra så beror på att \( x^0 = 1\, \) enligt potenslagarna. Samma sak gäller för \( 12\, \) som också är en term därför att \( 12\, \) är lika med \( 12 x^0\, \). Därmed har vi identifierat både \( 4 x + 12\, \) och \( 3 x^2 + 5 x - 16\, \) som polynom.
I Matte 3c-kursen ska vi nu lära oss att hantera även polynom av högre grad än 2. Vi tar som exempel följande 4:e gradspolynomfunktion\[ y = x^4 - 29\;x^2 + 100 \] vars graf ser ut så här:
Som man ser är grafen mer komplicerad än parabeln. Den har mer minima och maxima och mer nollställen som inte av en tillfällighet är identiska med lösningarna till 4:e gradsekvationen \( x^4 - 29\;x^2 = -100 \). Vi gjorde om denna ekvation till funktionen ovan så att ekvationens lösningar blev funktionens nollställen.
Ett polynoms nollställen
När polynomets värde blir 0 kallar man de x för vilka polynomets värde blir 0, polynomets nollställen. Till skillnad från polynomets värde där vi satt in ett tal för x och fick ett värde för polynomet, måste vi nu vända på steken och sätta polynomet till ett värde, närmare bestämt till värdet 0 och beräkna x. Det är en mycket svårare uppgift eftersom vi måste lösa en ekvation som i regel är av högre grad. Vi är ju ute efter de x för vilka ett polynom av en viss grad blir 0. Dessa x är polynomets nollställen. Därför kan ett polynom ha flera nollställen medan ett polynoms värde är alltid unikt.
Exempel:
Bestäm alla nollställen till polynomet \( 5\,x^2 -\,20\,x \).
Att beräkna polynomets nollställen innebär att sätta polynomet till 0 och lösa följande ekvation\[ 5\,x^2 -\,20\,x = 0 \]
Eftersom vänsterledet saknar konstant term kan man bryta ut x som är den gemensamma faktorn i båda termer för att sedan kunna använda nollproduktmetoden\[\begin{align} 5\,x^2 -\,20\,x & = 0 \\ x\,(5\,x -\,20) & = 0 \\ x_1 & = 0 \\ 5\,x_2 -\,20 & = 0 \\ x_2 & = 4 \\ \end{align}\]
Polynomets nollställen är alltså \( x_1 = 0\, \) och \( x_2 = 4\, \).
En familj av polynom
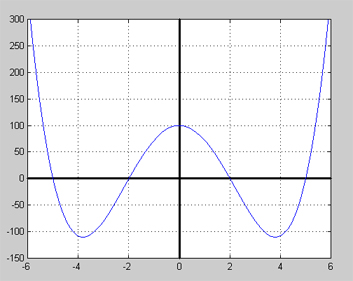
Ett polynoms grad är ett mått på dess kompexitet. Ett exempel på hur kompexiteten växer med graden (från 0 till 5) är följande sex polynom vars grafer är ritade i samma koordinatsystem:
Fil:Chebyshev Polyn 2nd 60.jpg
Man ser att kurvorna får fler maxima/minima ju högre deras grad är. Dessa polynom heter Chebyshevpolynom av 2:a slag efter den ryske matematikern Chebyshev som presenterade dem 1854. Att vi kallar dem för en familj av polynom beror på att de är relaterade till varandra med följande formel:
- \[ U_n(x) = 2\,x\,\cdot\,U_{n-1}(x)\,-\,U_{n-2}(x) \qquad\qquad n = 2, 3, ... \]
- \[ U_0(x) = 1, \quad U_1(x) = 2\,x \]
Om vi tittar på tabellen ovan ser man att polynomen \( U_n(x) \) bildar en följd där varje polynom har ett nummer n, kallat index (subscript som är skrivet nedsänkt). Formeln ovan ger oss möjligheten att ta fram Chebyshevpolynomen successivt, dvs vi kan ställa upp ett polynom med hjälp av de två föregående. I princip kan man ställa upp alla Chebyshevpolynom med denna formel utgående från de två första som är givna. Låt oss börja med att ställa upp det tredje (OBS! n = 2) med hjälp av de två första (n = 0 och 1)\[ \displaystyle U_0(x) = \underline{1} \]
\( U_1(x) = \underline{2\,x} \)
För n = 2 ger formeln ovan\[ U_2(x) = 2\,x\,\cdot\,U_1(x)\,-\,U_0(x) = 2\,x\,\cdot\,2\,x\,-\,1 = \underline{4\,x^2\,-\,1} \]
Sedan kan vi få fram \( U_3(x) \) genom att att sätta in n = 3 i formeln ovan\[ U_3(x) = 2\,x\,\cdot\;U_2(x)\,-\,U_1(x) = 2\,x\,\cdot\,(4\,x^2\,-\,1)\,-\,2\,x = 8\,x^3\,-\,2\,x\,-\,2\,x = \underline{8\,x^3\,-\,4\,x} \]
För n = 4 ger formeln ovan \( U_4(x) \) osv.\[ U_4(x) = 2\,x\,\cdot\,U_3(x)\,-\,U_2(x) = 2\,x\,\cdot\,(8\,x^3\,-\,4\,x)\,-\,(4\,x^2\,-\,1) = 16\,x^4\,-\,8\,x^2\,-\,4\,x^2\,+\,1 = \underline{16\,x^4\,-\,12\,x^2\,+\,1} \]
Så här kan man fortsätta för att få fram alla Chebyshevpolynom. Eftersom formeln som används bygger på att beräkna ett polynom från de två föregående kallar man den för polymens rekursionsformel, ett begrepp som används i samband med följder och summor (kap 5). Man kan säga att följden av Chebyshevpolynomen definieras av rekursionsformeln ovan.
Jämförelse av koefficienter
Med likhet mellan polynom menar man en algebraisk identitet mellan polynomen. Två polynom av samma grad:
- \[ P(x) = a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + \quad \ldots \quad + a_1 \cdot x + a_0 \]
och
- \[ Q(x) = b_n \cdot x^n + b_{n-1} \cdot x^{n-1} + \quad \ldots \quad + b_1 \cdot x + b_0 \]
är lika med varandra om alla deras motsvarande koefficienter, dvs de som tillhör termer av samma grad, överensstämmer, närmare bestämt om:
- \[ a_n = b_n, \quad a_{n-1} = b_{n-1}, \quad \ldots \quad a_1 = b_1, \quad a_0 = b_0 \]
Exempel 1
Två polynom är givna\[ P(x) = a \cdot x + 2\,a + b \]
\( Q(x) = 2\,x + 1\!\, \).
För vilka värden på \( a\, \) och \( b\, \) är de två polymen lika med varandra?
Vi skriver \( P(x),\, \) och \( Q(x)\, \) så att vi lättare kan se motsvarande koefficienter\[ P(x) = a \cdot x^1 + (2\,a + b) \cdot x^0 \]
\( Q(x) = 2 \cdot x^1 + \quad\;\; 1 \quad\;\; \cdot x^0 \)
Jämförelse av koefficienterna till \( x^1\, \) leder till\[ a = 2\,\]
Jämförelse av koefficienterna till \( x^0 \,\) leder till\[ 2\,a + b = 1\!\,\]
Sätter man in \( a = 2\, \) i denna relation får man \( b = -3\, \).
Polynomen \( P(x)\, \) och \( Q(x)\, \) är lika med varandra för\[ a = 2\, \]
\( b = -3\, \)
Metoden kallas jämförelse av koefficienter och är ett viktigt verktyg för att lösa högre gradsekvationer genom att faktorisera högre gradspolynom, se övningarna 10 och 11.
Exempel 2
Problem: Följande 3:e gradspolynom är givet\[ P(x) = x^3 + 4\,x^2 + x - 26 \]
Hitta ett 2:a gradspolynom \( Q(x)\, \) så att:
- \[ Q(x)\cdot (x-2) = P(x) \]
Svar: \( Q(x) = x^2 + 6 \, x + 13 \)
Lösning:
Det 2:a gradspolynomet \( Q(x)\, \) kan skrivas så här\[ Q(x) = a\,x^2 + b\,x + c \]
Vi bestämmer koefficienterna \( a\, , \, b\, \) och \( c\, \) så att \( Q(x)\cdot (x-2) = P(x) \)
\(\begin{align} Q(x) \cdot (x - 2) & = (a\,x^2 + b\,x + c)\cdot (x - 2) = a\,x^3 - 2\,a\,x^2 + b\,x^2 - 2\,b\,x + c\,x - 2\,c = \\ & = a\,x^3 + (b - 2\,a)\,x^2 + (c - 2\,b)\,x - 2\,c = \\ & = a \cdot x^3 + (b - 2\,a) \cdot x^2 + (c - 2\,b) \cdot x - 2\,c \cdot x^0 \\ P(x) & = 1 \cdot x^3 + \quad\;\; 4 \quad\;\; \cdot x^2 + \quad\;\; 1 \quad\;\; \cdot x - 26 \cdot x^0 \end{align} \)
Jämförelse av koefficienterna till \( x^3 \)-termen ger:
- \[\begin{align} a & = 1 \end{align} \]
Jämförelse av koefficienterna till \( x^2 \)-termen ger:
- \[\begin{align} b - 2\, a & = 4 \\ b - 2\cdot 1 & = 4 \\ b - 2 & = 4 \\ b & = 6 \\ \end{align} \]
Jämförelse av koefficienterna till \( x^1 \)-termen ger:
- \[\begin{align} c - 2\, b & = 1 \\ c - 2\cdot 6 & = 1 \\ c - 12 & = 1 \\ c & = 13 \\ \end{align} \]
Jämförelse av koefficienterna till \( x^0 \)-termen bekräftar värdet på c:
- \[\begin{align} - 2\,c & = - 26 \\ c & = 13 \\ \end{align} \]
Vi får \( a = 1\, , \, b = 6\, \) och \( c = 13\, \) och därmed\[ Q(x) = x^2 + 6 \, x + 13 \]
Internetlänkar
http://www.mathsisfun.com/algebra/polynomials.html
http://www.youtube.com/watch?v=IDpnNnjFB1c
http://www.coolmath.com/algebra/algebra-practice-polynomials.html
http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut6_poly.htm
http://tutorial.math.lamar.edu/Classes/Alg/Polynomials.aspx
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.