3.3 Terasspunkter

<-- Förra avsnitt

Teori

Övningar

--> Nästa avsnitt

Lektion 31 Kurvkonstruktion med derivata I

Lektion 32 Kurvkonstruktion med derivata II

Terasspunkter

I förra avsnitt lärde vi oss två metoder för att hitta en funktions extrempunkter dvs maxima eller minima:

• Funktionens derivata \( \, = \, 0 \, \) och andraderivatan \( \, < \, 0 \, \) eller \( \, > \, 0 \, \) dvs \( \, \neq \, 0 \, \).

• Funktionens derivata \( \, = \, 0 \, \) och derivatan byter tecken kring sitt nollställe.

Båda metoder uteslöt följande alternativ:

• Både funktionens derivata och andraderivata \( \, = \, 0 \, \).

• Funktionens derivata \( \, = \, 0 \, \) och derivatan inte byter tecken kring sitt nollställe.

Dessa alternativ tar vi upp nu: Vad händer om funktionens derivata och andraderivata är \( \, 0 \, \) eller om derivatan är \( \, 0 \, \) och bibehåller sitt tecken kring nollstället?

Ett sådant fall föreligger i följande enkelt exempel:

\[\begin{array}{rcl} f(x) & = & x^3 \\ f'(x) & = & 3\,x^2 \\ f''(x) & = & 6\,x \end{array}\]

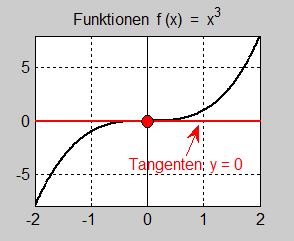
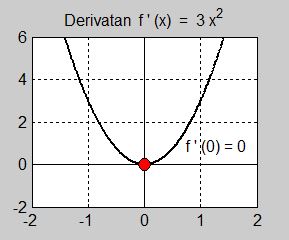
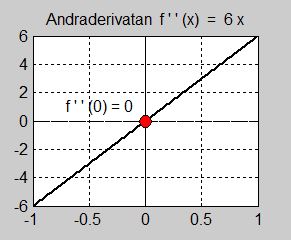
Vi ska undersöka funktionen \( \, f(x) = x^3 \, \) i och kring punkten \( \, x = 0 \, \) genom att titta på följande grafer:

            

Funktionens graf till vänster visar att det inte föreligger en extrempunkt i \( x = 0 \), varken ett maximum eller ett minimum. Det handlar snarare om en typ av kritisk punkt som är ny för oss. Kritiskt, därför att \(-\) precis som hos extrempunkter \(-\) tangenten till kurvan i denna punkt är horisontell dvs har lutningen \( \, 0 \, \). Denna nya typ av kritisk punkt kallas terasspunkt.

Bilden i mitten visar att derivatan har ett nollställe i \( \, x = 0 \, \). Det speciella med detta nollställe är att kurvan inte skär \( \, x\)-axeln utan bara berör den. Med andra ord, \( \, x = 0 \, \) är en dubbelrot till andragradsfunktionen \( \, f'(x) = 3\,x^2 \, \). Detta gör att derivatan inte byter tecken kring \( \, x = 0 \, \) utan är positiv både till vänster om och till höger om nollstället. Att derivatan är positiv innebär i sin tur att själva funktionen \( \, f(x) = x^3 \, \) är växande både till vänster om och till höger om \( \, x = 0 \, \) \(-\) ett kännetecken för terasspunkter.

Bilden till höger visar att även andraderivatan har ett nollställe i \( \, x = 0 \, \). Till skillnad från derivatans nollställe är detta nollställe av enkel typ, vilket framgår av att grafen verkligen skär \( \, x\)-axeln dvs byter tecken kring \( \, x = 0 \, \). I självaste punkten \( \, x = 0 \, \) är andraderivatan varken positiv eller negativ, varav följer att \( \, x = 0 \, \) inte är någon extrempunkt för funktionen \( \, f(x) = x^3 -\) ytterliare ett kännetecken för terasspunkter.

Vi har inte ritat grafen till tredjederivatan \( \, f'''(x) = 6 \), men den är \( \neq 0 \, \) vilket \(-\) och det är det nya hos terasspunkter \(-\) är ett nödvändigt villkor för att funktionen har en terasspunkt i \( \, x = 0 \, \). Därmed lämnar vi vårt enkla exempel och kommer till det allmänna fallet:

Regler om terasspunkter

Tre kriterier behövs för att få reda på en funktions terasspunkt: ett om derivatans nollställen, det andra om andraderivatans nollställen och det tredje om att tredjederivatan inte får vara \( \, 0 \, \). Alla tre måste vara uppfyllda. Generellt gäller nämligen:

:

Derivatans och andraderivatans nollställen samt att tredjederivatan \( \, \neq 0 \, \) avgör för vilka \(\, x \) en funktion har terasspunkter:

Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har en terasspunkt i \( {\color{White} x} x = a {\color{White} x} \) om \( {\color{White} x} f\,'(a) \, = \, f\,''(a) \, = \, 0 {\color{White} x} \) och \( {\color{White} x} f\,'''(a) \, {\bf {\color{Red} \neq}} \, 0 {\color{White} x}. \)

---

Om \( {\color{White} x} f\,'(a) \, = \, f\,''(a) \, = \, 0 {\color{White} x} \) och \( {\color{White} x} f\,'''(a) \, {\bf {\color{Red} =}} \, 0 {\color{White} x} \) har funktionen ingen terasspunkt i \( {\color{White} x} x = a {\color{White} x} \). Endast ett teckenstudium kan avgöra den kritiska punktens typ.

Reglerna ovan säger i ord:

Där derivatan är \( \, 0 \) och andraderivatan är negativ har funktionen ett maximum. Där derivatan är \( \, 0 \) och andraderivatan är positiv har funktionen ett minimum. Där både derivatan och andraderivatan är \( \, 0 \) föreligger varken ett maximum eller ett minimum. Vad som gäller då behandlas i nästa avsnitt.