Kapitel 4 Integraler

Utdrag ur planeringen:

Fil:Planering Integraler Rubrik.jpg

Fil:Planering Integralera.jpg

4.1 Primitiva funktioner

Genomgång: \( \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \) Övningar: Boken, sid 175

\( \quad \)

Hastighetsmätaren deriverar.

Trippmätaren integrerar.

Fil:0 Diff vs Integr 260.jpg

\( \qquad \)

Fil:1 Primitiva funktioner 30.jpg

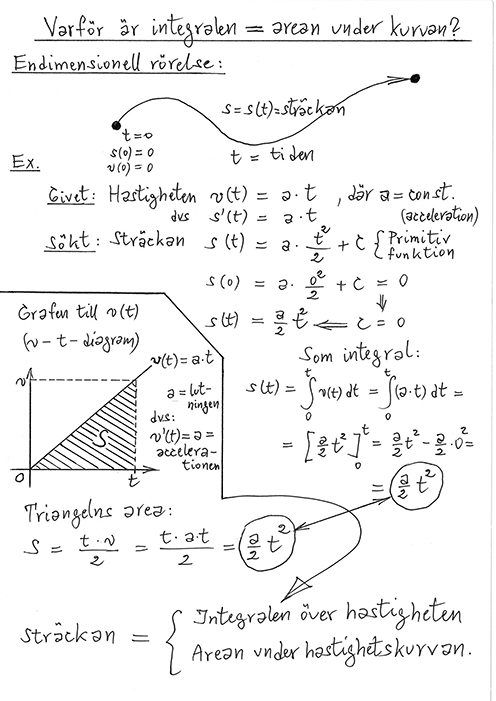
Integration är den inversa operationen till derivering. \( \quad \) Primitiv funktion = "Anti"derivata

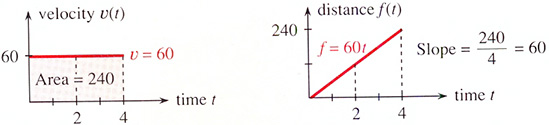
Fysikalisk tolkning: \( \quad\; \) Derivata = Hastighet \( \qquad\qquad\quad\;\;\; \) Integral = Sträcka

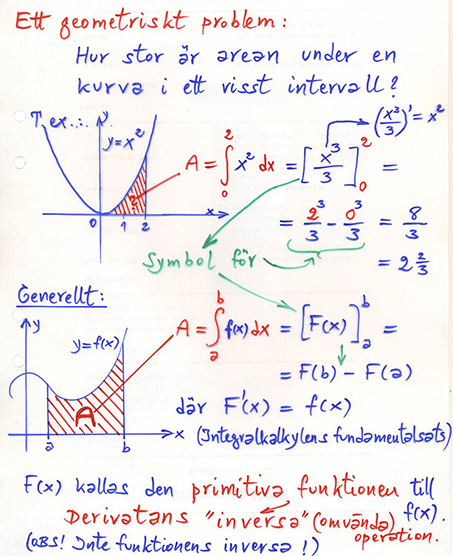
Geometrisk tolkning: \( \;\; \) Derivata = Kurvans lutning \( \qquad\quad\;\; \) Integral = Area under kurvan

Algebraisk tolkning: \( \quad \) Derivata = Limes av differenskvot \( \quad \) Integral = Limes av oändlig summa

Derivata	Integral
a) Hastighet	Sträcka
b) Kurvans lutning	Area under kurvan
c) Limes av differenskvot	Limes av oändlig summa
d) \( \, 0,00403 \, \)	Tre
e) \( \, 1,006 \, \)	Fyra

Ex. på "Integral = Area under kurvan" : \( \quad \) Rörelse med konstant hastighet 60 km/h

OBS! Area under kurvan är det inversa till kurvans lutning (eng. slope).

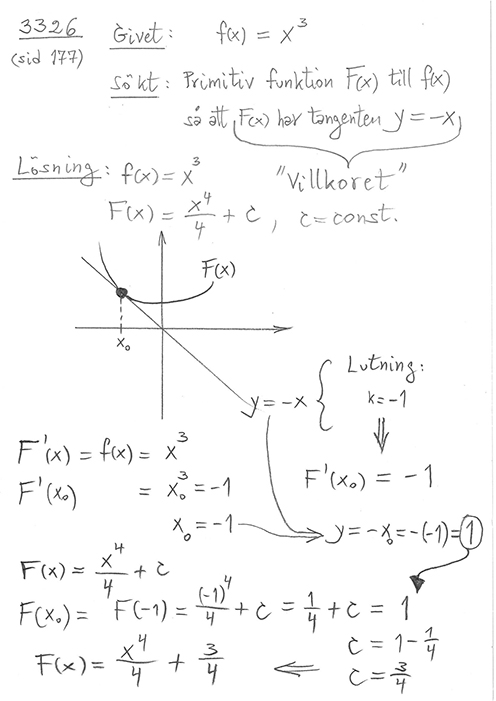
Sammanfattning:

Givet: \( \quad f\,(x) \)

Sökt: \( \quad \) Primitiv funktion \( \; F\,(x) \quad \) så att \( \quad F\,'\,(x) = f\,(x) \)

Ex.:

\( f\,(x) \; = \; x\,^3 \)

\( F\,(x) \, = \, \displaystyle \frac{x\,^4}{4} + C \; , \quad C = {\rm const.} \)

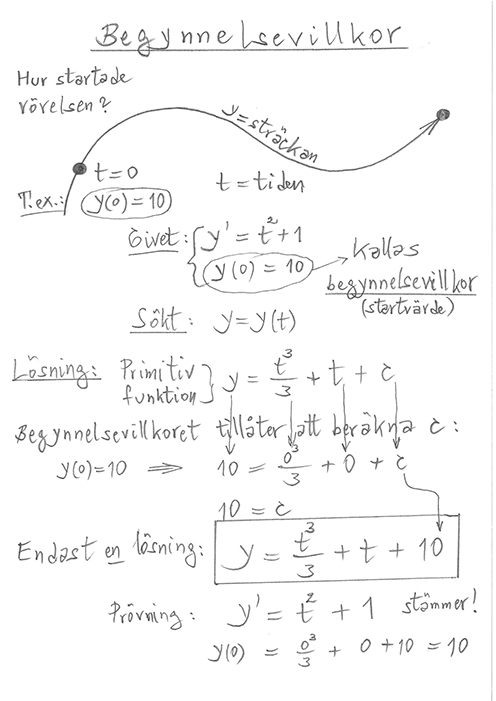
\( \;\qquad\; C \; \) kallas för integrationskonstanten och bestäms av villkor (krav) som ställs på \( \, F\,(x) \, \). \( \quad {\bf {\color{Red} {\downarrow}}} \quad \)