3.2 Lokala maxima och minima
| <-- Förra avsnitt | Teori | Övningar | --> Nästa avsnitt |
Regler om maxima och minima
:
Derivatans nollställen och andraderivatans förtecken avgör för vilka \(\, x \) en funktion har maxima och minima:
Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett maximum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och andraderivatan \( {\color{White} x} f\,''(a) \, {\bf {\color{Red} <}} \, 0 {\color{White} x}. \)
Funktionen \( {\color{White} x} y \, = \, f(x) {\color{White} x} \) har ett minimum i \( {\color{White} x} x = a {\color{White} x} \) om derivatan \( {\color{White} x} f\,'(a) \, = \, 0 {\color{White} x} \) och andraderivatan \( {\color{White} x} f\,''(a) \, {\bf {\color{Red} >}} \, 0 {\color{White} x}. \)
Med andraderivatan menas derivatans derivata. Man får andraderivatan genom att derivera derivatans funktion ett steg till. Sammanlagt har man då deriverat den ursprungliga funktionen två gånger.
Med derivatan menas alltid första derivatan. Med maximum menas en funktions största och med minimum en funktions minsta värde.
Där derivatan är \( \, = \, 0 {\color{White} x} \) och andraderivatan är negativ har funktionen ett maximum.
Där derivatan är \( \, = \, 0 {\color{White} x} \) och andraderivatan är positiv har funktionen ett minimum.
Vilka slutsatser man kan dra när både första- och andraderivatan är \( \, = \, 0 {\color{White} x} \) behandlas senare.
I grafen till exemplet nedan visas en funktion som har ett minimum. Men hur avgörs detta algebraiskt och framför allt hur hittas detta minimum dvs hur beräknas för vilket \(\, x \) funktionen antar sitt minsta värde?
Exempel 1 Vinternattens kallaste tidpunkt
Vi återgår till Exempel 1 i förra avsnitt, men byter frågeställning: Vi tittar inte längre på funktionens växande eller avtagande utan på funktionens minsta värde (minimum):
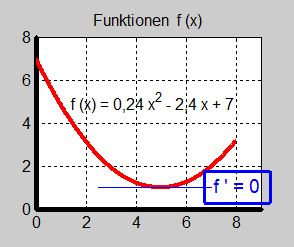
Under en vinternatt varierar temperaturen enligt funktionen \( {\color{White} x} \; y \, = \, f(x) \, = \, 0,24\,x^2\,-\,2,4\,x\,+\,7 {\color{White} x} \; \) med definitionsområdet: \( \quad 0 \leq x \leq 8 \).
där \( y \; = \) temperaturen i grader Celsius och
\( x \; = \) tiden i timmar efter midnatt
a) Bestäm nattens kallaste tidpunkt.
b) Bestäm nattens lägsta temperatur.
Lösning:
a) För att kunna använda reglerna om maxima och minima ställer vi upp första- och andraderivatan:
- \[ f(x) \, = \, 0,24\,x^2 - 2,4\,x + 7 \]
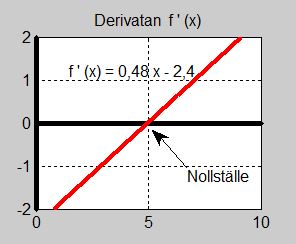
- \[ f'(x) \, = \, 0,48\,x - 2,4 \]
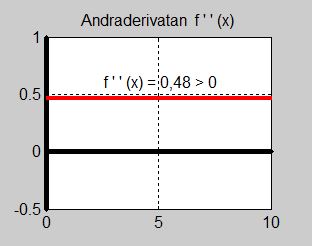
- \[ f''(x) \, = \, 0,48 \]
Graferna till dessa tre funktioner visas ovan.
För att få reda på derivatans nollställe som regeln kräver sätter vi derivatan till \( \, 0 \) och beräknar tidpunkten \( x \, \) då derivatan blir \( \, 0 \):
- \[\begin{array}{rcrcl} f'(x) & = & 0,48\,x - 2,4 & = & 0 \\ & & 0,48\,x & = & 2,4 \\ & & x & = & {2,4 \over 0,48} \\ & & x & = & 5 \end{array}\]
Nu vet vi att derivatan blir \( \, 0 \) i \( x = 5 \, \) dvs tangenten till kurvan \( y = f(x) \, \) är horisontell i \( x = 5 \, \). Men en horisontell tangent kan vara ett maximum eller ett minimum. För att avgöra om det föreligger ett maximum eller ett minimum kräver regeln andraderivatans förtecken. Därför sätter vi \( x = 5 \, \) in i andraderivatan och kollar om den blir positiv eller negativ:
- \[ f''(5) = 0,48 \,>\, 0 \]
Andraderivatan är positiv (konstant) för alla \( x \, \) och därmed även för \( x = 5 \, \). Därav följer att \( f(x) \, \) har ett minimum i \( x = 5 \, \).
Alltså är nattens kallaste tidpunkt kl 5.
b) Temperaturen vid kl \( 5 \, \) är:
- \[ f(5) = 0,24 \cdot 5^2 - 2,4 \cdot 5 + 7 = 1 \]
Alltså är nattens lägsta temperatur 1 grad Celsius.